6.4. Ізольовані особливі точки та їх класифікація

Точка називається ізольованою особливою точкою функції , якщо дана функція аналітична в деякому околі цієї точки, за винятком самої точки (в проколотому околі).

Класифікація ізольованих особливих точок здійснюється за характером розвинення функції в ряд Лорана

;

в (проколотому) околі особливої точки . При цьому можливі три випадки:

а) Головна частина ряду Лорана відсутня (в ряді не має чле­нів з від’ємними степенями різниці ), тобто

.

Тоді називається усувною особливою точкою.

При цьому , тобто в усувній особливій точці функція має скінченну границю.

Якщо доозначити функцію в точці рівністю , то функція стане аналітичною в точці , а відповідний ряд буде рядом Тейлора для функції . Оскільки , то в околі усувної особливої точки функція обмежена.

б) Головна частина ряду Лорана членів, тобто

.

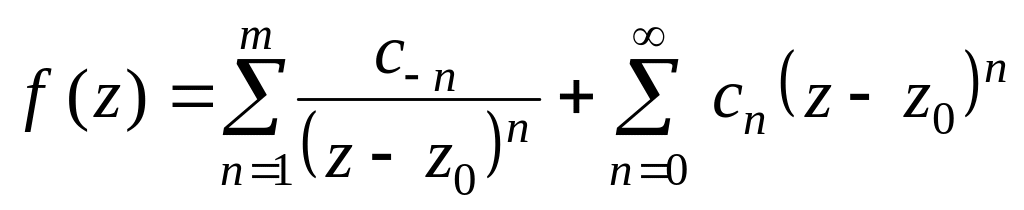Тоді називається полюсом -го порядку. Полюс першого порядку також називають простим полюсом.

Ясно, що коли точка – полюс -го порядку функції , то для функції ця точка є усувною особливою. Тоді . Тому

,

тобто в полюсі функція має нескінченну границю. Порядком полюса служить найбільше натуральне значення , при якому існує скінченна границя .

Якщо точка – полюс -го порядку функції , то для функції ця точка служить -кратним коренем. Справедливе також обернене твердження.

в) Головна частина ряду Лорана має нескінченну кількість членів, тобто

.

Тоді називається істотно особливою точкою.

В істотно особливій точці функція не має границі ні скінченної, ні нескінченної. У залежності від вибору шляху прямування точки до точки функція буде мати різні границі.

Нескінченно віддалена точка. Особлива точка на­зивається ізольованою особливою точкою, якщо функція аналітична в круговому кільці (зовні кола ) – в проколотому околі нескінченно віддаленої точки . Функція в околі нескінченно віддаленої точки розвивається в ряд Лорана за степенями :

.

(зміст і назви частин ряду протилежні тим, що мають місце для ряду Лорана з центром у скінченній точці).

Ізольована особлива точка називається: а) усув­ною особливою точкою, якщо ряд Лорана не містить додатних степенів ; б) полюсом -го порядку, якщо найбільша додатна степінь в ряді Лорана дорівнює ; в) істотно особливою точкою, якщо ряд Лорана має нескінченну кількість додатних членів.

Наприклад, для функції точка – полюс -го порядку, а для функції точка – істотно особлива.

Приклад. Знайти всі особливі точки функції та визначити їх характер:

.

Розв’язання. Знайдемо точки, де функція не визначена: , , , , , . Дослідимо поведінку функції в околі кожної з цих точок.

:

;

– усувна особлива точка.

: ;

; – полюс другого порядку.

: ;

;

– простий полюс.

: ;

;

– простий полюс.

: – не

існує, оскільки не існує ;

– істотно особлива точка.

: – не

існує, оскільки не існує ;

– істотно особлива точка.

Зауваження. Особливі точки можуть бути неізольованими. Наприклад, функція має полюси . Тому в довільному околі особливої точки є інші особливі точки. Початок координат є точкою згущення полюсів цієї функції.