5. Інтеграл функції комплексної змінної

5.1. Поняття комплексного інтеграла

Нехай функція неперервна та однозначна в деякій області , а – будь-яка кусково-глад­ка крива в цій області (рис. 22). Розіб’ємо цю криву довільним чином на елементарних дуг точками у напрямку від точки до точки . Кожній елементарній дузі відповідає елементарна хорда . На кожній елементарній дузі виберемо довільну точку і складемо інтегральну суму для функції на кривій .

Г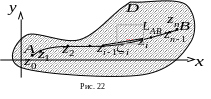 раниця інтегральної суми при необмеженому здрібненні розбиття (незалежно від способу розбиття та вибору точок) називається інтегралом (контурним інтегралом) комплексної функції по кривій (контуру) :

,

де – диференціал комплексного аргументу.

Інтеграл від комплексної функції можна виразити через два дійсні криволінійні інтеграли за координатами:

.

Тому для інтеграла від комплексної функції справедливі відповідні властивості криволінійних інтегралів. Зокрема, при зміні напряму обходу кривої цей інтеграл тільки змінює знак:

.

Як і для дійсних криволінійних інтегралів, обчислення інтеграла від комплексної функції зводиться за допомогою методу заміни змінної до обчислення звичайного визначеного інтеграла.

Приклад. Обчислити заданий інтеграл по вказаній дузі:

а) ; – коло.

б) ;

– дуга параболи.

Розв’язання.  а)

.

б)

.

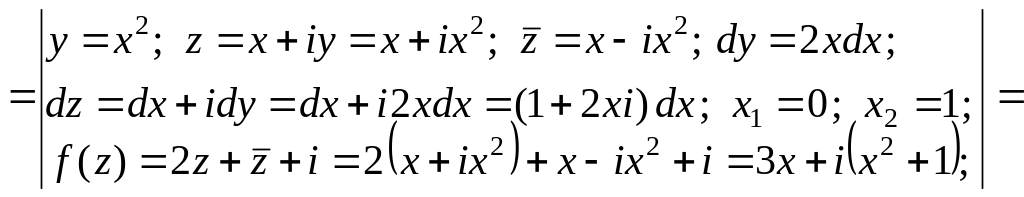
Зауваження. Для існування інтеграла досить неперервності підінтегральної функції , тому інтеграл може існувати і у випадку неаналітичності цієї функції.

5.2. Первісна функції комплексної змінної. Інтегральна теорема Коші

Якщо крива лежить в області аналітичності функції , то комплексний інтеграл не залежить від форми шляху інтегрування, а тільки від початкової та кінцевої точок. Це пояснюється тим, що для аналі­тич­ної функції виконуються умови Коші–Рімана і , які співпадають з умовами незалежності від шляху інтегрування обох відповідних дійсних криволінійних інтегралів і .

Таким чином, інтеграл аналітичної функції можна подати у вигляді .

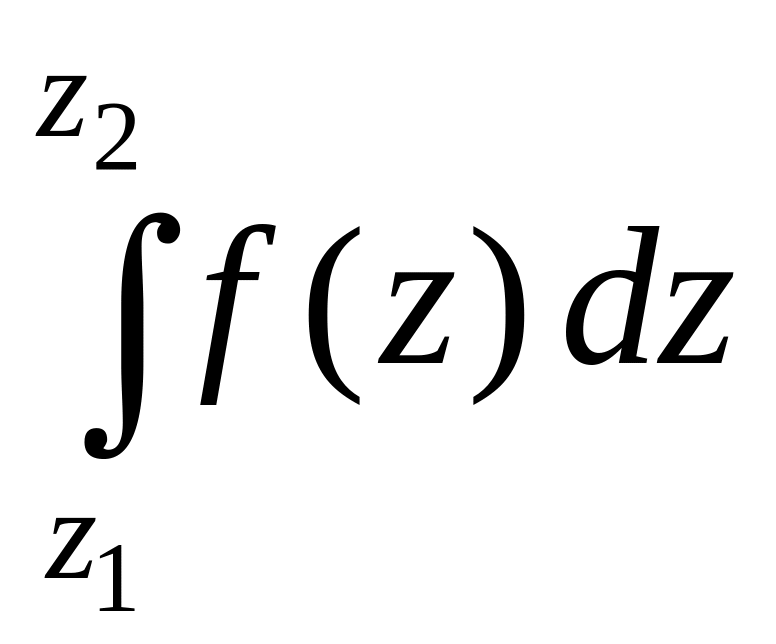Якщо зафіксувати нижню межу інтегрування, то одер­жа­ний інтеграл , як функція верхньої межі, слу­жить первісною для :

.

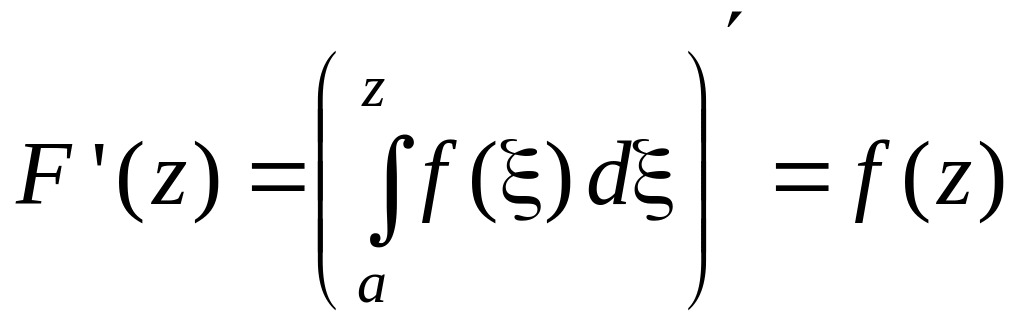Множина всіх первісних для даної функції утворює відповідний невизначений інтеграл.

Для інтеграла аналітичної функції справджується формула Ньютона – Лейбніца

,

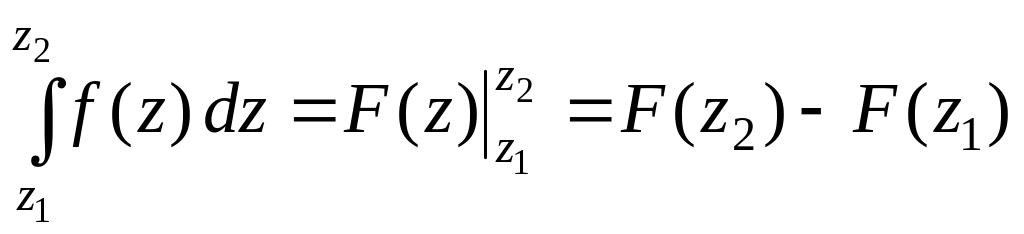де – довільна первісна.

Зауваження. Таблиця інтегралів аналогічна відповідній таб­лиці для функцій дійсного аргументу, але підлогарифмові ви­рази не містять модулю.

Приклад. Користуючись таблицею інтегралів, обчислити за­даний інтеграл аналітичної функції:

.

Розв’язання. 

.

Умови незалежності криволінійного інтеграла від форми шляху інтегрування еквівалентні рівності нулю цього інтеграла по довільному замкненому контуру , що лежить в даній однозв’язній області

.

Аналогічне твердження справедливе для комплексного інтеграла аналітичної функції.

Теорема (інтегральна теорема Коші для однозв’язної області). Якщо функція аналітична в однозв’язній області , що обмежена кусково-гладким контуром і неперервна в замкненій об­ласті , то інтеграл функції по контуру дорівнює нулю

.

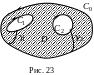
Теорема Коші поширюється на багатозв’язну область (рис. 23): якщо функція аналітична в багатозв’язній об­ласті , що обмежена зовнішнім контуром і внутрішніми контурами , і неперервна в замкненій області , то інтеграл функції по повній межі області в додатному напрямі дорівнює нулю

.

Іншими словами, для складеного контуру справедливо: інтеграл функції по зовнішньому контуру дорівнює сумі інтегралів по всіх внутрішніх контурах при умові, що обіг усіх контурів здійснюється проти годинникової стрілки

.

При доведенні багатозв’язна область перетворюється в однозв’язну область за допомогою розрізів , що з’єд­нують внутрішні контури із зовнішнім (рис. 23). Кожна лінія роз­різу проходиться двічі в протилежних напрямах, тому ін­тег­рали по ній при додаванні взаємно знищуються.