Контрольні запитання

2.1 Які припущення відносно геометричного та фізичного стану стержня слід зробити при виведенні рівняння, яке б описувало поздовжні коливання, що виникають у ньому під час розтягу або стиску внаслідок прикладених зусиль?

2.2 На які фізичні закони спираються при виведенні хвильово-

го рівняння, що описує поздовжні коливання стержня?

2.3 Вигляд хвильового рівняння у випадку важкого стержня.

2.4 З чого складається постановка задачі математичної фізики про поздовжні коливання стержня?

2.5 Що задають та характеризують початкові умови?

2.6 На що вказують крайові умови? Різновиди крайових умов.

Лекція 3 поперечні коливання струни

3.1 Поперечні коливання скінченної струни. Виведен-ня хвильового рівняння

Розглянемо туго натягнуту струну із закріпленими кінця-ми. Якщо вивести її із стану рівноваги, то почнуться коливан-ня струни. При вивченні цього коливального процесу зробимо ряд припущень щодо геометричного і фізичного стану струни:

1. струна скінченна завдовжки l;

2. діаметр поперечного перерізу d набагато менший за довжину струни l, тобто ним можна знехтувати і вважати, що є тільки один характерний розмір – довжина;

3. струна однорідна, тобто лінійна густина

4. струна пружна, тобто має місце закон Гука;

5. коливання поперечні, тобто всі точки струни рухають-

ся перпендикулярно до її положення рівноваги, причому у будь-який момент струна лежить в одній площині;

6. коливання малі, тобто малі відхилення точок струни від положення рівноваги;

7. зовнішні сили неперервно розподілені вздовж струни і діють перпендикулярно до положення рівноваги струни;

8. сила натягу струни у всіх точках є величиною сталою (T=const) і напрямленою по дотичній до струни.

Виведемо рівняння поперечних коливань струни. Введемо систему координат , у якій струну розмістимо на осі .

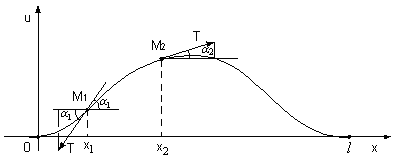Рисунок 3.1 – Нескінченно малий елемент струни М₁, М₂, спроектований на інтервал

Вважаємо, що кінці струни ( та ) закріплені нерухомо. Якщо струну вивести із положення рівноваги (від-тягнути, або ударити по ній), то кожна її точка переміститься на деяку величину . Розглянемо нескінченно малий елемент струни М₁М₂, який проектується на інтервал . На цей елемент діють сили натягу T, які замінюють відкинуті частини струни (Рисунок 3.1). Знайдемо проекції сил на вісь ou:

. (3.1)

Оскільки коливання малі, то кути та теж малі, тому мають місце наступні перетворення (з точністю до нескінченно малих вищих порядків):

;

.

Тоді сила натягу струни

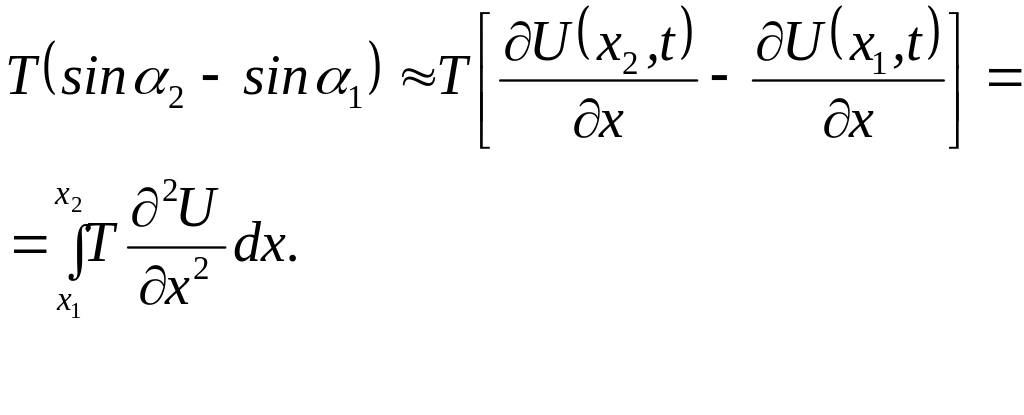(3.2)

Сила натягу належить до внутрішніх сил. Припустимо, що на одиницю довжини струни діє зовнішня сила з інтенсив-ністю . Елементарна сила, що діє на елементарну довжину струни з проекцією дорівнює , а на виділений елемент : .

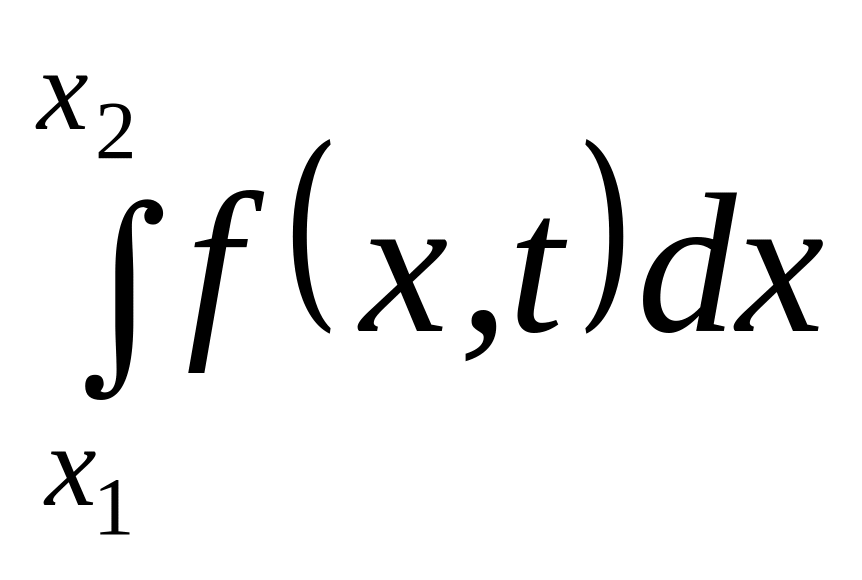Зовнішня сила вважається додатною, якщо вона діє вгору, і від’ємною, якщо – вниз.

Тепер, згідно другого закону Ньютона (сума всіх діючих на рухомий об’єкт сил дорівнює добутку його маси на прискорення), маємо:

або .

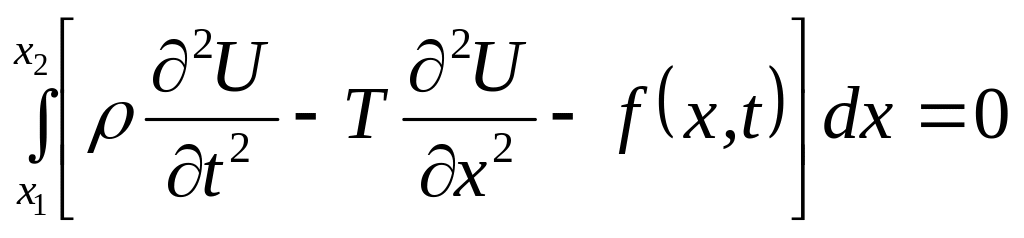За основною лемою математичної фізики маємо:

або, поділивши на ,

. (3.3)

Введемо такі позначення: ; Тоді отримаємо хвильове рівняння для поперечних коливань струни:

, . (3.4)

Зазначимо, що – розв’язок цього рівняння, що визначає положення будь-якої точки струни у будь-який момент часу , тобто визначає форму струни.

Знайдемо вільний член , пов’язаний з наявністю зовнішніх сил, у випадку важкої струни. Середня інтенсивність сили тяжіння для елемента : .

Інтенсивність в точці струни

Тоді , а хвильове рівняння набуває вигляду:

, . (3.5)

Якщо то коливання називаються вільними, а якщо то – вимушеними.

З фізичної точки зору коефіцієнт – це швидкість розповсюдження поперечної хвилі, що підтверджується його розмірністю:

. Отже, .