
- •1.1 Предмет математичної фізики. Диференціальні рівняння з частинними похідними
- •1.2 Зведення до канонічного виду диференціального рівняння другого порядку
- •Контрольні запитання
- •2.1 Поздовжні коливання стержня. Виведення хвильового рівняння
- •2.2 Постановка задачі математичної фізики про поздовжні коливання стержня
- •Контрольні запитання
- •3.1 Поперечні коливання скінченної струни. Виведен-ня хвильового рівняння
- •3.2 Постановка задачі про поперечні коливання скінченної струни
- •3.3 Постановка задачі про поперечні коливання нескінченної струни
- •Контрольні запитання
- •4.1 Поперечні коливання нескінченної струни
- •4.2 Поперечні коливання скінченної струни
- •4.3 Фізичний зміст розв’язку задачі про поперечні коливання
- •4.4 Вимушені коливання струни
- •Контрольні запитання
- •5.1 Метод Фур’є для розв’язування задачі про поздовжні коливання стержня
- •Контрольні запитання
- •6.1 Задача про розповсюдження тепла. Рівняння теплопровідності
- •6.2 Постановка задачі теплопровідності
- •6.3 Метод Фур’є для розв’язування задачі теплопровідності
- •6.4 Стаціонарні процеси. Рівняння Лапласа
- •6.5 Задача Діріхле
- •6.6 Задача Неймана
- •6.7 Мішана задача
- •6.8 Рівняння Лапласа в циліндричних координатах
- •6.9 Задача діріхле для круга
- •Контрольні запитання
- •7.1 Застосування операційного числення при розв’язуванні диференціальних рівнянь з частинними похідними
- •6) Властивість диференціювання зображення
- •7) Властивість інтегрування зображення
- •7.2 Зображення згортки
- •7.3 Схема побудови розв’язку диференційного рівняння з частинними похідними
- •Контрольні запитання
6.6 Задача Неймана
задача
Неймана (друга крайова задача)
формулюється так: знайти
функцію
яка задовольняє всередині замкненої
поверхні
рівняння Лапласа та її похідна по
напрямку зовнішньої нормалі
![]() у кожній точці М
поверхні
набуває заданих значень:
у кожній точці М
поверхні
набуває заданих значень:
К.У.![]() (6.41)
(6.41)
Нагадуємо, що похідна пов’язана з потоком тепла через поверхню . Аналогічно формулюється задача Неймана для двовимірного та одновимірного випадків.
6.7 Мішана задача
Мішана
задача (третя крайова задача) формулюється
так: знайти функцію
![]() яка задовольняє всередині замкненої
поверхні
рівняння Лапласа, а у кожній точці М
поверхні
виконується умова:
яка задовольняє всередині замкненої
поверхні
рівняння Лапласа, а у кожній точці М
поверхні
виконується умова:
К.У.
![]() (6.42)
(6.42)
де
функції
![]() та
та
![]() є заданими. Цю задачу ще назива-
є заданими. Цю задачу ще назива-
ють задачею з косою похідною.
6.8 Рівняння Лапласа в циліндричних координатах
Нехай
![]() – гармонічна в деякій області
функція трьох змінних. Тоді для неї
рівняння Лапласа має вигляд:
– гармонічна в деякій області
функція трьох змінних. Тоді для неї
рівняння Лапласа має вигляд:
![]() (6.43)
(6.43)
Введемо
у розгляд циліндричні координати
![]() які пов’язані з декартовими координатами
формулами
які пов’язані з декартовими координатами
формулами
![]()
![]()
![]() ,
,![]() (6.44)
(6.44)
Звідси зворотній зв’язок:
![]()
![]()
![]() (6.45)
(6.45)
Щоб записати рівняння Лапласа в циліндричних корди-натах, знайдемо відповідні частинні похідні функції , використовуючи формули диференціювання складеної функ-ції декількох змінних:
![]()
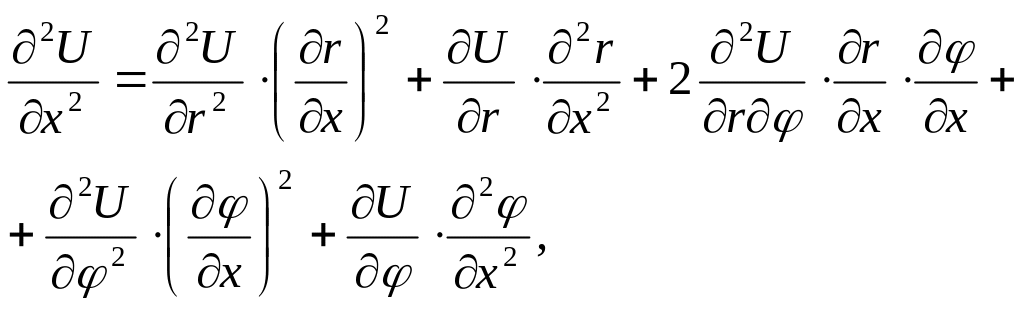
![]()
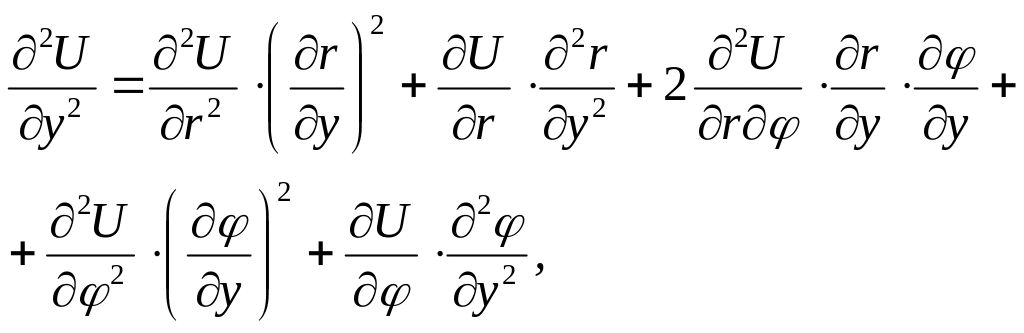
![]()
![]()
Враховуючи, що:
![]()
![]()
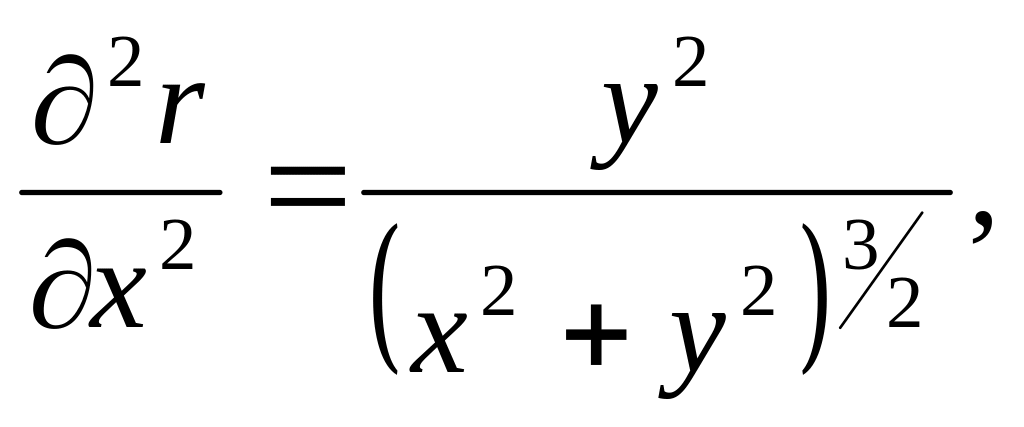
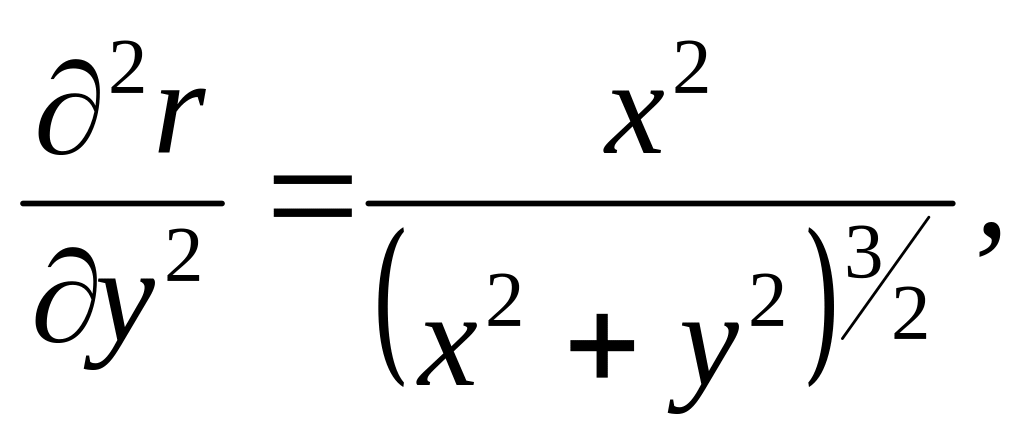
![]()
![]()
![]()
![]()
отримаємо:
![]() (6.46)
(6.46)
Це і є рівняння Лапласа в циліндричних координатах.
Якщо функція U не залежить від z, а лише від x та y, то рівняння Лапласа буде мати вигляд
![]() (6.47)
(6.47)
де r
та
![]() – полярні координати на площині. Знайдене
рівнян-
– полярні координати на площині. Знайдене
рівнян-
ня є рівнянням Лапласа в полярних координатах.
Приклад
6.3 Знайдемо розв’язок
рівняння Лапласа в області D,
що обмежена двома колами
![]() та
та
![]() якщо значення шуканої функції на колах:
якщо значення шуканої функції на колах:
К.У.
![]()
![]()
де
![]() та
та
![]() – сталі.
– сталі.
Це може бути, наприклад, задача про стаціонарний розподіл температури у кільці між двома колами, якщо на самих колах температура задана.
Розв’язуємо задачу у полярних координатах. Очевидно, шукана функція не залежить від кута . Тоді рівняння Лапласа набуває простішого вигляду:
![]()
Це звичайне диференціальне рівняння другого порядку, яке допускає пониження порядку. Інтегруючи його, знайдемо
![]()
Визначимо
![]() та
та
![]() із крайових умов:
із крайових умов:
![]()
звідси
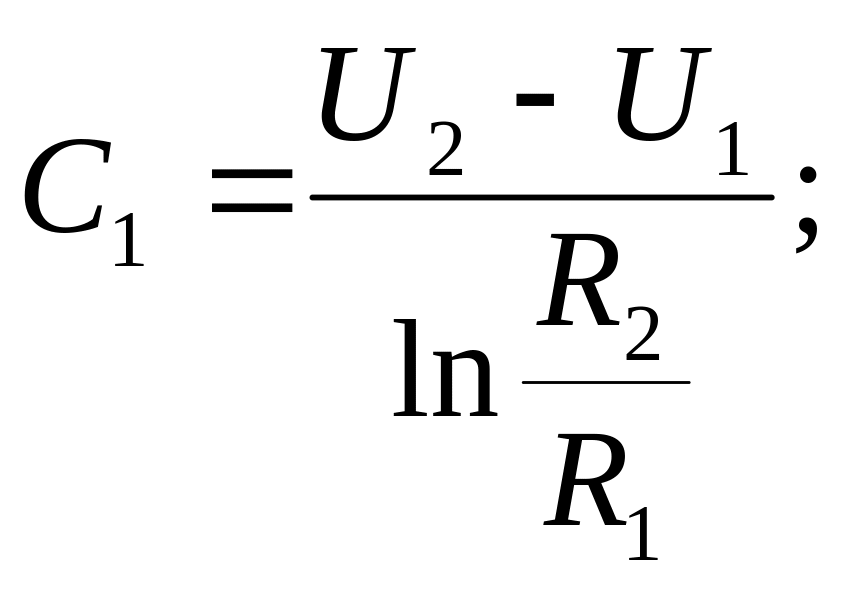

остаточно отримаємо :
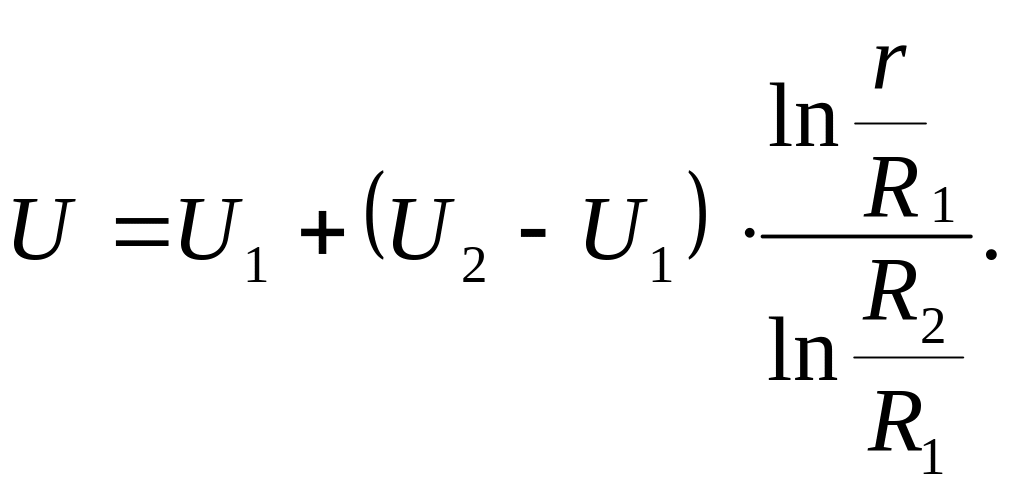
6.9 Задача діріхле для круга
Нехай
у площині хоу
є круг радіуса R з центром в початку
координат. на
його колі задана деяка функція
![]() де
– полярний кут. Треба
знайти функцію
де
– полярний кут. Треба
знайти функцію
![]() неперервну у крузі, яка задовольняє
всередині круга рівнянню Лапласа [1].
Постановка задачі в полярних координатах
має вигляд:
неперервну у крузі, яка задовольняє
всередині круга рівнянню Лапласа [1].
Постановка задачі в полярних координатах
має вигляд:
![]() ,
,
![]() ,
,
К.У.
![]()
Припустимо,
що
![]() можна розкласти в ряд Фур’є на
можна розкласти в ряд Фур’є на
![]() .
Перепишемо рівняння Лапласа, домноживши
його на
.
Перепишемо рівняння Лапласа, домноживши
його на
![]() :
:
![]()
Будемо
шукати розв’язок за методом Фур’є,
подаючи функцію
![]() у вигляді добутку двох функцій, кожна
з яких залежить від однієї змінної:
у вигляді добутку двох функцій, кожна
з яких залежить від однієї змінної:
![]() (6.48)
(6.48)
Підставляючи її в рівняння та враховуючи, що
![]() та
та
![]() отримаємо:
отримаємо:
![]()
Відокремимо змінні:
![]()
Отже, рівняння Лапласа розпалося на два диференціаль-них рівняння:
![]() (І)
(І)
![]() .
(ІІ)
.
(ІІ)
З рівняння ( І ) маємо
k2+λ=0,
![]() .
.
Тоді
![]() (6.49)
(6.49)
Оскільки
задана область є кругом, то при збільшенні
кута
на 2π точка M(r,φ)
повернеться у своє початкове положен-ня.
Отже, функція Ф(φ)
– 2π-періодична, а це означає, що число
![]() має бути цілим:
має бути цілим:
![]() або
або
![]()
Тоді отримаємо множину функцій:
![]() ,
,
![]()
Коефіцієнти
![]() та
залишились невизначеними. Розглянемо
рівняння (ІІ):
та
залишились невизначеними. Розглянемо
рівняння (ІІ):
![]()
Розв’язок
цього рівняння будемо шукати у вигляді
![]() ,
де
– невідомий параметр. Підставимо цю
функ-цію у рівняння:
,
де
– невідомий параметр. Підставимо цю
функ-цію у рівняння:
![]() (6.50)
(6.50)
Поділивши
на
![]() ,
отримаємо:
,
отримаємо:
![]()
Зазначимо,
що
![]() – сторонній корінь, оскільки при
– сторонній корінь, оскільки при
![]() функція
функція
![]() Отже,
Отже,
![]() Остаточно маємо:
Остаточно маємо:
![]() (6.51)
(6.51)
Завдяки лінійності та однорідності рівняння Лапласа сума частинних розв’язків:
![]() (6.52)
(6.52)
буде також розв’язком рівняння Лапласа. Для знаходження коефіцієнтів та використаємо крайову умову:
![]()
Це є ряд
Фур’є для функції
з коефіцієнтами
![]() та
та
![]() які
визначаються за формулами Фур’є:
які
визначаються за формулами Фур’є:
![]()
![]()
Звідси:
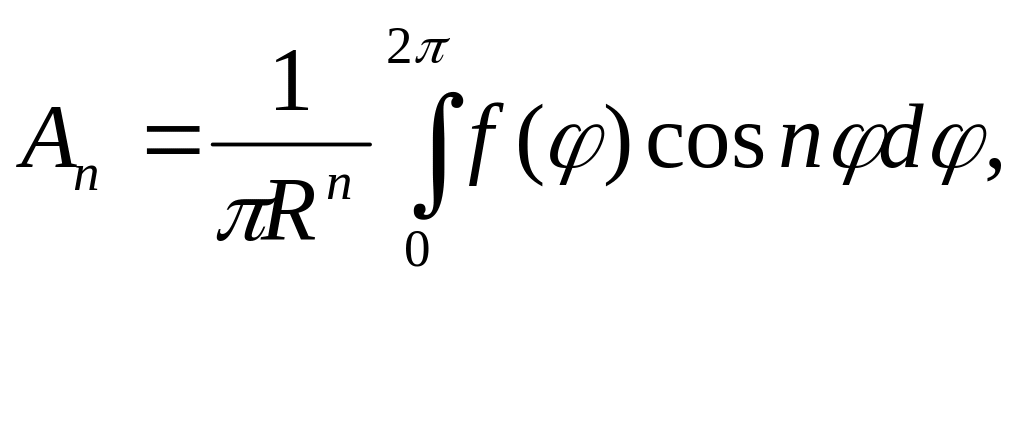
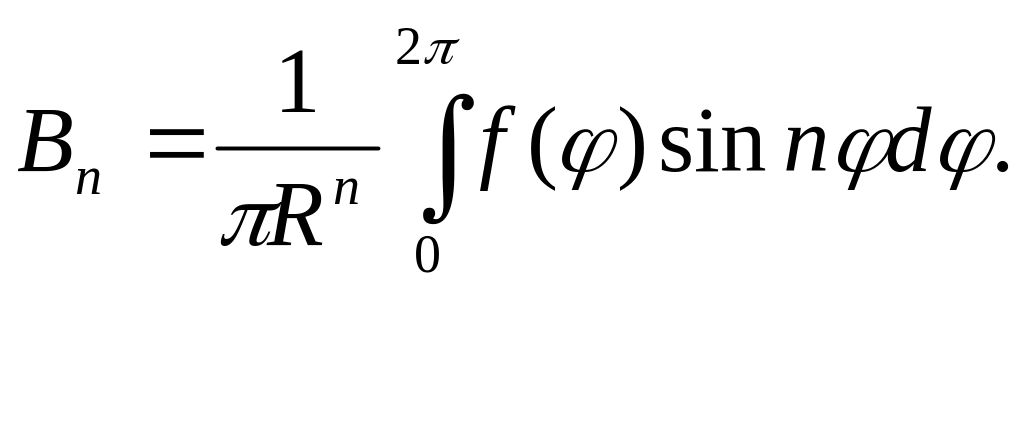 (6.53)
(6.53)
Таким чином, розв’язком задачі Діріхле у крузі радіуса R є функція (6.52) з коефіцієнтами (6.53).
