6.2 Постановка задачі теплопровідності

Із фізичних міркувань випливає, що для однозначного визначення температури в стержні довжиною , крім рівняння теплопровідності, необхідно задати додаткові три умови, які складаються з однієї початкової і двох крайових.

Початкова умова для рівняння теплопровідності задає розподіл температур у всіх точках стержня в деякий момент часу, який приймаємо за початковий . Початковий розподіл температур має вигляд:

П.У. U(x,0)=u|_t=0 = φ (х), (6.10)

де φ(х) – задана функція для всіх .

Крайові умови мають виконуватись там, де стержень може мати теплообмін з навколишнім середовищем, тобто на торцях стержня.

Нехай стержень лежить на осі Ох і один його кінець збігається з початком координат ( ), а другий має абсцису .

Крайові умови відображають тепловий режим на кінцях стержня і можуть задаватися по-різному. Розглянемо деякі з них. Нехай на кінцях стержня підтримується стала температура – на кінці і на кінці .

К.У. (6.11)

де – задані числа (можуть бути і нулі).

Запишемо загальніші граничні умови. використовуючи закон Ньютона, запишемо тепловий потік Р, що проходить через одиницю площі за одиницю часу пропорційно зміні температури на торці стержня:

, (6.12)

де h – коефіцієнт зовнішньої теплопровідності або коефіцієнт теплообміну, – температура на кінці стержня, – температура навколишнього середовища поблизу цього кінця.

При цьому потік вважається додатним, якщо тобто іде процес охолодження стержня. Отже, функція –спадна. А згідно з законом Фур’є цей самий потік пропорційний швидкості зміни температури в напрямку нормалі до торця:

(6.13)

Оскільки вектор нормалі паралельний до осі Ох, то для правого кінця потік буде:

a на лівому:

Тепер запишемо умови на лівому і правому кінцях стержня:

Г.У. . (6.14)

Тут , – задані температури навколишнього середовища поблизу відповідних кінців. Оскільки кінці стержня можуть знаходитися в різних середовищах, то сталі взято різними.

Розглянемо окремі випадки:

1. Нехай коефіцієнт теплообміну , тоді крайова умова

К.У. (6.15)

означає, що кінець стержня теплоізольований.

2. Нехай значення коефіцієнт теплообміну дуже вели-ке. Тоді, наприклад, для лівого кінця маємо:

, (6.16)

і, переходячи до границі при , отримаємо крайову умову

К.У. (6.17)

що означає вільний теплообмін з навколишнім середовищем на кінці х=0. Фактично, це те саме, що розглядалося в першому типі крайових умов.

3. На кінці стержня, не уточнюючи на якому, задається потік, як функція часу

(6.18)

П

Рисунок 6.1 – початковий розподіл температур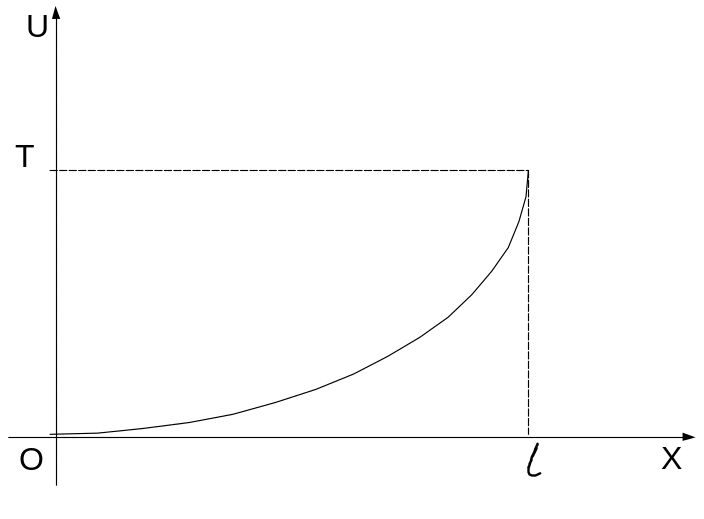

риклад 6.1 Поставити задачу про розповсюдження тепла в стержні, один кінець якого теплоізо-льваний, а на другому підтримується стала тем-пература T, причому в момент часу t=0 розподіл температур у стержні мав вигляд частини параболи з вершиною в початку координат, як зображено на рисунку 6.1.

Опишемо графік аналітично: . визначаємо коефіцієнт з того, що точка (l, T) задовольняє рівняння параболи. Отже, Тоді рівняння параболи має вигляд

Постановка задачі включає в себе написання рівняння теплопровідності, початкової та граничних умов

, ,

П.У. К.У.

Розв’язком цієї задачі є функція , яка задовольняє в указаній області рівняння теплопровідності, а також початкову і крайові умови.