Зміст

Вступ………………………………………………...............	5
Лекція 1 основні поняття математичної фізики. дифе-ренціальні рівняння з частинними похідними……………	7
1.1 Предмет математичної фізики. диференціальні рів-няння з частинними похідними……………………………	7
1.2 Зведення до канонічного виду диференціального рівняння другого порядку………………………………….	9
Лекція 2 Поздовжні коливання стержня…………………..	22
2.1 Поздовжні коливання стержня. Виведення хвильово-го рівняння…………………………………………………..	22
2.2 Постановка задачі математичної фізики про поз-довжні коливання стержня..……………………………….	26
Лекція 3 поперечні коливання струни……………………	33
3.1 Поперечні коливання скінченної струни. Виведення хвильового рівняння………………………………………..	33
3.2 постановка задачі про поперечні коливання скінченної струни..................................................................	36
3.3 Постановка задачі про поперечні коливання нескін-ченної струни……………………………………………….	38
Лекція 4 Методи розв’язування задач про коливання струни………………………………………………………..	41
4.1 Поперечні коливання нескінченної струни…………...	41
4.2 Поперечні коливання скінченної струни……………...	45
4.3 Фізичний зміст розв’язку задачі про поперечні коливання……………………………………………………	53
4.4 Вимушені коливання струни…………………………..	56
Лекція 5 Розв’язування задачі про поздовжні коливання стержня……………………………………………………...	65
5.1 Метод Фур’є для розв’язування задачі про поздовжні коливання стержня…………………………………………	65
Лекція 6 розповсюдження тепла…………………………..	72
6.1 Задача про розповсюдження тепла. Рівняння тепло-провідності………………………………………………….	72
6.2 Постановка задачі теплопровідності………………….	76
6.3 Метод Фур’є для розв’язування задачі теплопровід-ності………………………………………………………….	80
6.4 Стаціонарні процеси. Рівняння Лапласа………………	89
6.5 Задача Діріхле…………………………………………..	90
6.6 Задача Неймана……………………………....................	91
6.7 Мішана задача…………………………………………..	92
6.8 Рівняння Лапласа в циліндричних координатах……...	92
6.9 Задача діріхле для круга……………………………….	95
Лекція 7 Елементи операційного числення………………	100
7.1 Застосування операційного числення при розв’язу-ванні диференціальних рівнянь з частинними похідними	100
7.2 Зображення згортки…………………………………….	103
7.3 Схема побудови розв’язку диференціального рівнян-ня з частинними похідними………………………………..	105
Перелік використаних джерел	114

Вступ

Мета цього посібника – допомогти студентам глибше засвоїти матеріал таких спеціальних розділів, як „Рівняння ма-тематичної фізики” та „Операційне числення”. Математична фізика, як теорія математичних моделей фізичних явищ, займає особливе місце як у математиці, так і у фізиці. Перебуваючи на стику цих наук, математична фізика тісно зв'язана з фізикою в тій частині, яка стосується побудови математичної моделі, і в той самий час математична фізика – розділ математики, оскільки методи дослідження моделей є математичними.

Наприкінці XVII століття методи математичної фізики як теорії математичних моделей почали інтенсивно розроблятися в працях І. Ньютона щодо створення основ класичної механі-ки, всесвітнього тяжіння, теорії світла. Подальший розвиток методів математичної фізики (XVIII – перша половина XIX століття) і їхнє успішне застосування до вивчення математич-них моделей величезного обсягу різних фізичних явищ пов'я-зані з іменами Ж. Лагранжа, Л. Ейлера, П.Лапласа, Ж. Фур’є, К. Гауса, Б. Рімана, М. Остроградського та інших учених.

Великий внесок у розвиток методів математичної фізики зробили О. Ляпунов та В. Стєклов. З другої половини XIX століття методи математичної фізики успішно використовува-лися для вивчення математичних моделей фізичних явищ, пов'язаних з різними фізичними полями і хвильовими функ-ціями в електродинаміці, акустиці, теорії пружності, гідро- й аеродинаміці та інших напрямах дослідження фізичних явищ у суцільних середовищах. Математичні моделі цього класу явищ найчастіше описуються за допомогою диференціальних рівнянь з частинними похідними, що одержали назву рівняння математичної фізики.

У зв'язку з бурхливим розвитком електронної та обчислю-вальної техніки особливе значення для дослідження матема-тичних моделей фізики набувають прямі чисельні методи, і в першу чергу скінченно-різницеві методи розв’язування крайо-вих задач, що дозволило методами математичної фізики ефек-тивно вирішувати нові задачі газової динаміки, теорії перено-су, фізики плазми, у тому числі і зворотні задачі цих напрям-ків фізичних досліджень. Поряд із традиційними розділами математики стали широко застосовуватися теорія операторів, теорія узагальнених функцій, теорія функцій багатьох комп-лексних змінних, топологічні і алгебраїчні методи. Інтенсивна взаємодія теоретичної фізики, математики і використання комп’ютерів у наукових дослідженнях, привела до значного розширення математики, створення нових класів моделей і піднесла на новий рівень сучасну математичну фізику.

Постановка задач математичної фізики полягає в побудові математичних моделей шляхом виведення диференціальних, інтегральних або алгебраїчних рівнянь, що характеризувати-муть відповідний фізичний процес та описуватимуть основні закономірності досліджуваного класу явищ. При цьому вихо-дять з основних фізичних законів, що враховують тільки най-істотніші риси явища, відкидаючи низку його другорядних характеристик. Ефективним способом розв’язування диференціальних рівнянь з частинними похідними є викори-стання операційних методів, зокрема перетворення Лапласа.

Теоретичний матеріал цих розділів можна знайти в підручниках [1–6], тому даний конспект лекцій містить у вигляді довідкового матеріалу в рамках робочої програми для спеціальностей нафтогазової справи лише ті короткі відомості з теорії, які безпосередньо застосовуються при розв’язуванні задач.

Посібник буде корисним як студентам, так і викладачам, які ведуть практичні заняття з курсу математичної фізики.

Лекція 1 основні поняття математичної фізики. диференціальні рівняння з частинними похідними

1.1 Предмет математичної фізики. Диференціальні рівняння з частинними похідними

Предметом математичної фізики, як відомо [3], є вивчення методів розв’язування задач, що виникають при аналізі широкого класу фізичних явищ, які моделюються диференціальними рівняннями з частинними похідними. Ці рівняння називаються рівняннями математичної фізики. Ми не ставимо перед собою задачу вивчати всі способи розв’язування диференціальних рівнянь з частинними похідними. Розглянемо тільки ті конкретні рівняння, які є дуже важливими для фізики, механіки і техніки.

Зупинимось на основних поняттях таких рівнянь.

Диференціальним рівнянням з частинними похідними відносно невідомої функції називається рівняння, що зв’язує незалежні змінні , шукану функцію та її частинні похідні. Найвищий порядок частинної похідної, що входить в рівняння, називається порядком диференціального рівняння.

Наприклад, – є диференціальним рівнянням з частинними похідними 2-го порядку для функції класу .

Функція називається розв’язком диференціального рівняння з частинними похідними, якщо в результаті підстановки її в рівняння воно перетворюється в тотожність.

Приклад 1.1 Знайти функцію , яка є розв’язком диференціального рівняння .

Домножимо обидві частини рівняння на і зінтегруємо по змінній :

,

де – довільна функція від (ця функція відіграє роль довільної сталої при інтегруванні по ).

Знову домножимо обидві частини рівняння на та проінтегруємо по :

У результаті отримаємо

,

де – друга довільна функція від .

Перевіркою легко встановити, що знайдена функція задовольняє задане рівняння, отже, є його розв’язком.

Як бачимо, функція залежить від двох довільних двічі диференційовних функцій та У цьому і полягає відмінність розв’язування диференціальних рівнянь з частинними похідними у порівнянні з розв’язуванням диференціальних рівнянь зі звичайними похідними, де розв’язок залежить від довільних сталих. Знайдена функція є загальним розв’язком даного диференціального рівняння з частинними похідними.

Диференціальне рівняння з частинними похідними називається лінійним, якщо шукана функція і всі її частинні похідні входять в рівняння лінійно. Рівняння з частинними похідними називається квазілінійним, якщо воно лінійне відносно всіх старших похідних від невідомої функції.

Диференціальні рівняння математичної фізики, якими ми будемо займатись в подальшому, мають між собою чимало спільного [1]: усі вони – другого порядку, лінійні відносно невідомої функції та її частинних похідних, а коефіцієнти перед функцією та її похідними – сталі числа. Загальний вигляд таких рівнянь для функції є наступним:

,

де – сталі, а права частина – задана функція від .

1.2 Зведення до канонічного виду диференціального рівняння другого порядку

Розглянемо диференціальне рівняння з частинними похідними, яке є лінійним відносно похідних другого поряд-ку:

(1.1)

де A, B, C – сталі (в загальному випадку можуть бути і функціями, визначеними в деякій області D площини xOy з неперервними похідними до другого порядку включно), F – неперервна функція [4].

Л. Ейлер довів, що будь-яке диференціальне рівняння виду (1.1) за допомогою заміни незалежних змінних і можна привести до одного з трьох видів (типів), відомих як гіперболічний, параболічний та еліптичний (по аналогії з теорією кривих другого порядку в курсі аналітичної геометрії) [1].

Поставимо задачу: за допомогою заміни змінних x і y звести рівняння (1.1) до найпростішого (канонічного) виду. Введемо нові змінні

(1.2)

Нехай функції і – двічі неперервно-диференційовані і якобіан

в області D.

Виразимо похідні через нові змінні:

, ;

Підставляючи ці похідні в (1.1), отримаємо:

(1.3)

де

Явний вираз нас не цікавить. Спробуємо вибрати функції і так, щоб деякі із коефіцієнтів , , стали рівними нулю. Очевидно, щоб вирішити питання про рівність нулю коефіцієнтів та , достатньо розв'язати еквівалентне завдання про розв'язок наступного диференціального рівняння першого порядку відносно деякої функції z(x, y), яку будемо називати характеристичною функцією:

(1.4)

Поділивши (1.4) на отримаємо квадратне рівняння відносно

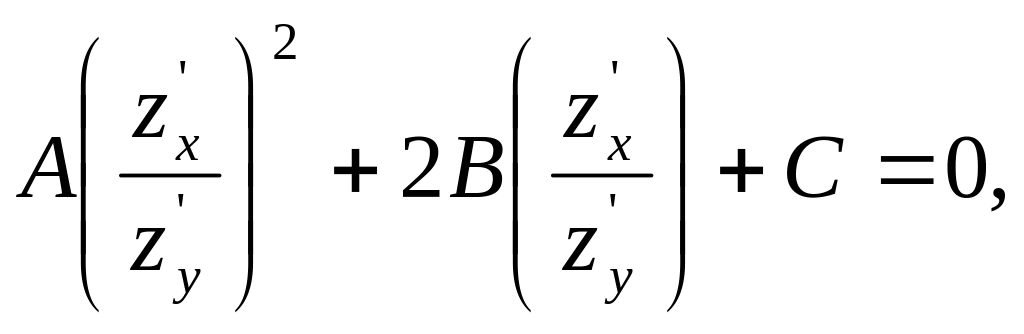
яке фактично розпадається на два:

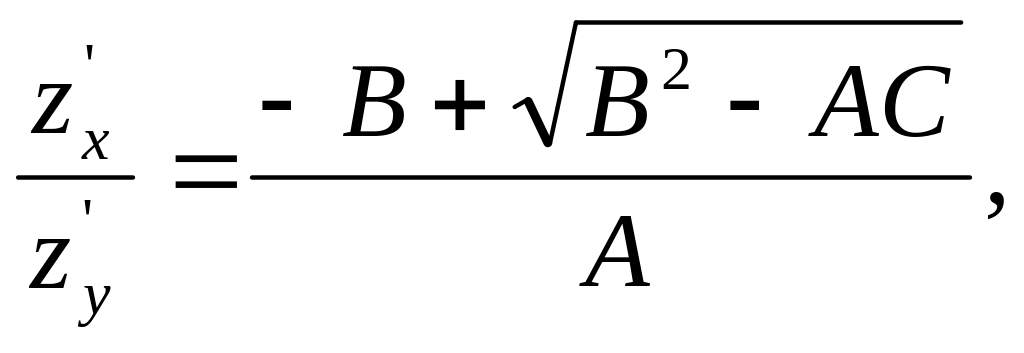(1.5)

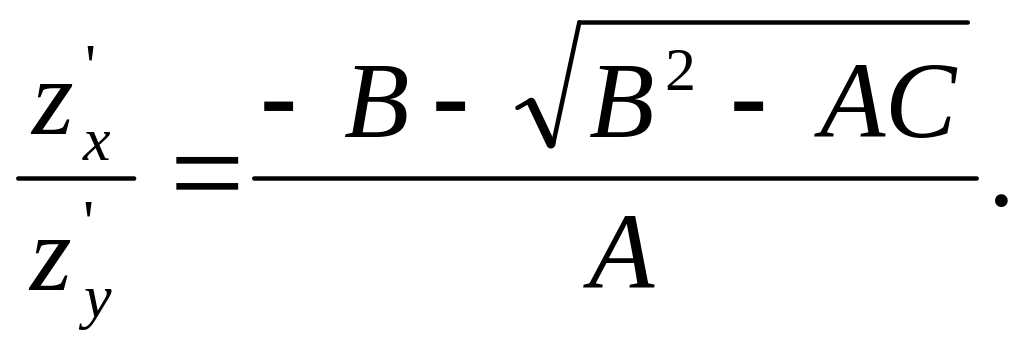(1.6)

Криву z(x, y)=const, що є розв’язком рівняння (1.4) будемо називати характеристичною кривою, а саме рівняння (1.4) − рівнянням характеристик.

З умови z(x, y)= const випливає, що

z'_x dx+ z'_y dy = 0.

Звідси маємо простий зв'язок з похідними функції z(x, y)

Ввівши відповідну заміну в (1.5) і (1.6), отримаємо :

(1.7)

(1.8)

Розв'язки рівнянь (1.5) і (1.6) пов'язані з розв'язком рівнянь (1.7) і (1.8) наступним чином. Нехай

, (1.9)

− загальні інтеграли рівнянь (1.7) і (1.8).

Тоді функції і будуть розв'язками рівнянь (1.5) і (1.6) відповідно, а значить і розв'язками рівняння (1.4). Криві (1.9) називаються характеристиками рівняння (1.1). Зазначимо, що рівняння (1.7) і (1.8) у загальнішій формі можна подати у вигляді одного характеристичного рівняння:

А(dy)²−2Bdxdy+C(dx)²=0. (1.10)

Очевидно, що розв’язки рівнянь (1.7) і (1.8), а значить канонічний вид рівняння (1.1), залежить від знаку дискримінанта D=В²−АС, або знаку визначника

у всій області .

У залежності від цього розглянемо три випадки:

1) Нехай у розглядуваній області ∆ < 0 (D = В²−АС >0) − рівняння гіперболічного типу (можна вважати, що або , або ).

У цьому випадку загальні інтеграли (1.9) визначають дві дійсних і різних сім'ї характеристик. Оскільки функції φ(x, y) і ψ(x, y) задовольняють рівняння (1.4), то, поклавши в (1.2)

, , (1.11)

отримаємо (оскільки знак дискримінанта не змінюється при заміні змінних).

Розділивши рівняння (1.3) почленно на 2В, одержимо канонічний вид рівняння гіперболічного типу:

.

При рівняння (1.1) належить гіперболічному типу і вже має канонічний вид. Якщо рівняння (1.1) було лінійним відносно похідних першого порядку і самої функції , то після перетворення рівняння також буде лінійним. Якщо в цьому рівнянні покласти , , то рівняння набуде вигляду:

.

Це другий канонічний вид рівняння канонічного типу.

2) Нехай ∆=0 (D=В²−АС=0) – рівняння параболічного типу. В силу вказаної умови можна припустити, що в кожній точці розглядуваної області один з коефіцієнтів , відмінний від нуля. Нехай .

У цьому випадку загальні інтеграли (1.9) дійсні і співпа-дають. Таким чином, є тільки одна сім'я характеристик. Рівняння (1.5) і (1.6) також співпадають і набувають вигляду

Не важко бачити, що будь-який розв’язок цього рівняння в силу задовольняє також рівняння:

Врахувавши це, маємо ξ= φ(x, y), а за η(x, y), візьмемо будь-яку двічі неперервнодиференційовну функцію, для якої якобіан

Тоді . Враховуючи, що D = 0 ( а це означає що і ), отримаємо, що , а коефіцієнт набуває виду

Поділивши рівняння (1.3) на одержимо канонічне рівняння параболічного типу:

.

Зауважимо, якщо , а , то отримали б аналогічне канонічне рівняння з зліва.

3) Нехай ∆>0 (D=В²−АС <0) − рівняння еліптичного типу.

Тут загальні інтеграли (1.9) є комплексними величинами. Тобто рівняння еліптичного типу не мають дійних характеристик. Нехай φ(x, y)≡ φ₁(x, y)+ іφ₂(x, y)= С₁ − один із загальних інтегралів (1.9); другий загальний інтеграл буде комплексно спряженим з даним.

Покладемо в (1.2):

ξ= φ₁(x, y) , η=φ₂(x, y).

Підставляючи в рівняння (1.4) його розв'язок φ=ξ+іη, отримаємо

Відокремлюючи у цій тотожності дійсну та уявну частини, одержимо:

Звідси випливає, що . Очевидно, що . Тоді отримаємо рівняння еліптичного виду:

Приклад 1.2 Знайти загальний розв’язок рівняння, звівши його до канонічного виду

.

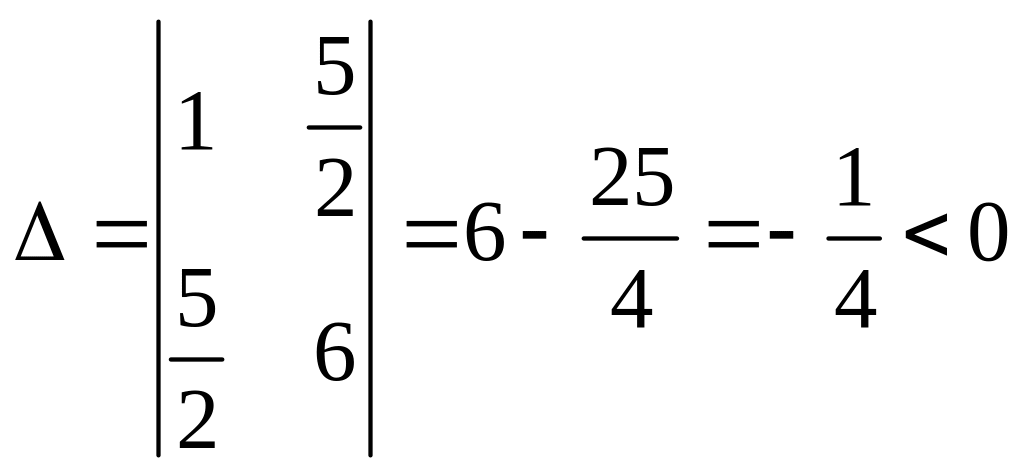Тут . Отже, задане рівняння гіперболічного типу.

Запишемо рівняння характеристик

.

Поділивши на , отримаємо

.

Знайдемо .

Розв’яжемо ці рівняння.

,

.

Введемо заміну змінних

або

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

Підставивши у задане рівняння, отримає-мо

.

Після спрощень одержуємо .

Інтегруємо по змінній (можна по ). Тоді , де – довільна функція змінної .

Інтегруємо обидві частини по

де і – довільні двічі диференційовні в розглядуваній області функції. Повертаючись до змінних отримаємо Це і буде загальним розв’язком заданого рівняння.

Приклад 1.3 Знайти загальний розв’язок рівняння, звівши його до канонічного виду

.

Тут . Отже, задане рівняння параболічного типу.

Запишемо рівняння характеристик

.

Поділивши на , отримаємо

.

Знайдемо .

.

Звідси .

Введемо заміну змінних: .

За другу нову змінну візьмемо, наприклад, (очевидно, що і незалежні).

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

;

;

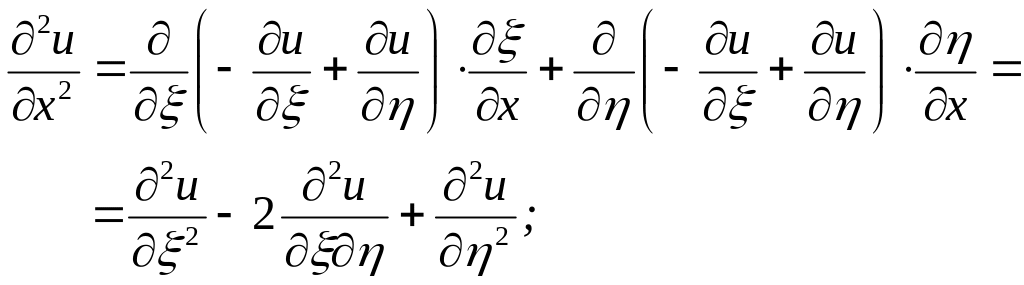
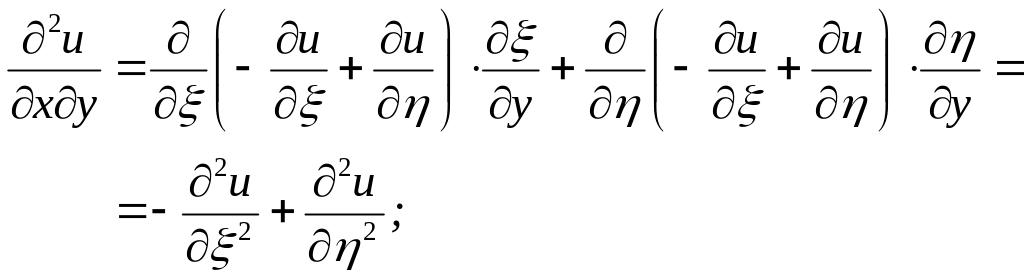
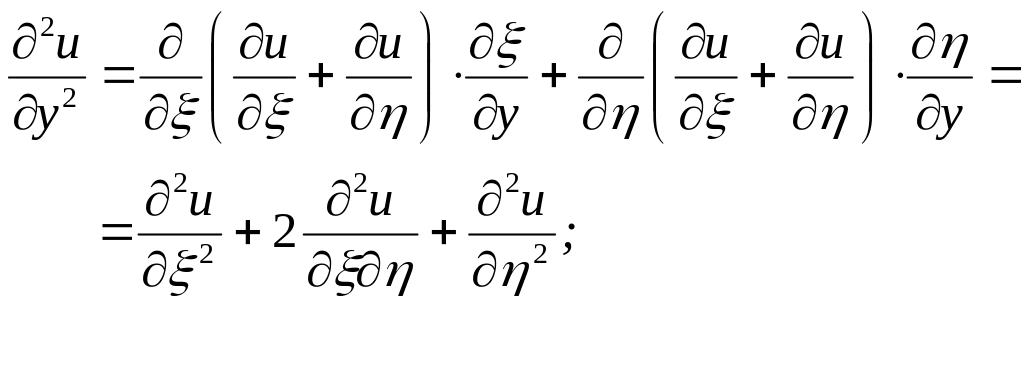
Підставивши у задане рівняння, після спрощень отримаємо .

Інтегруємо двічі по змінній :

, ,

де – довільні функції змінної .

Повертаючись до змінних отримаємо . Це і буде загальним розв’язком заданого рівняння.

Приклад 1.4 Звести до канонічного виду рівняння

.

Тут . Отже, задане рівняння еліптичного типу.

Запишемо рівняння характеристик

.

Поділивши на , отримаємо

.

Знайдемо .

.

Звідси

Введемо заміну змінних:

– один із загальних інтегралів, другий буде спряженим до нього;

Тоді , .

Знайдемо всі частинні похідні, що входять у задане рівняння, виразивши їх через :

;

;

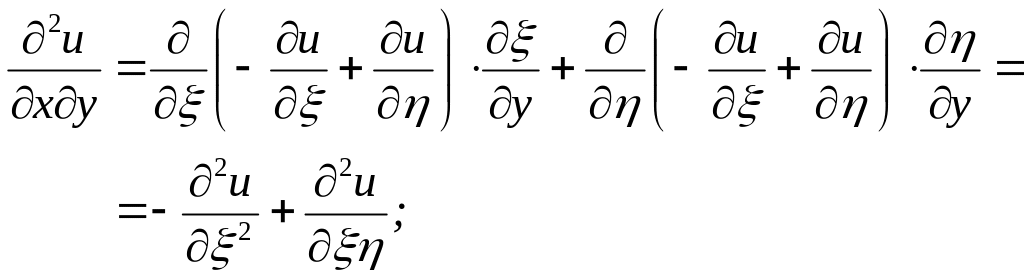
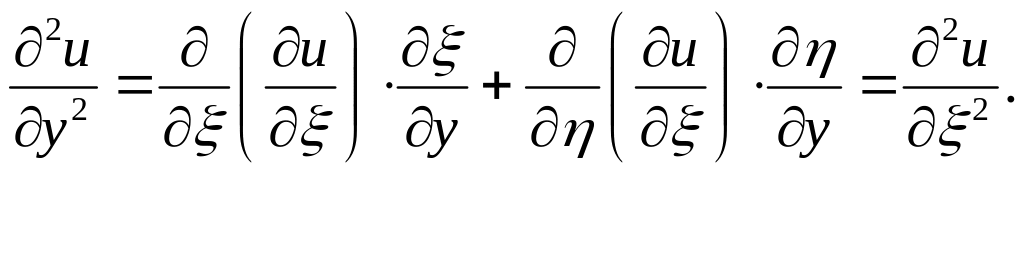
Підставивши у задане рівняння, після спрощень отримаємо його у канонічному виді:

.

Зауваження: наведена класифікація лінійних рівнянь зі сталими коефіцієнтами переноситься і на рівняння зі змінними коефіцієнтами, які в нашому посібнику не розглядаються.