
- •1. Математика як наука і як навчальний предмет. Історія розвитку математики. Роль математичних знань, умінь і навичок
- •2. Математичні поняття і математичні речення.
- •3. Означення та їх структура.
- •4.Висловлення і висловлювальна форма.
- •5. Квантори.
- •6. Правила побудови заперечень висловлень, що містять квантори.
- •9. Дедуктивне міркування.
- •10. Найпростіші схеми дедуктивних міркувань. Неповна індукція.
- •13.Поняття множини.Способизадання множин.
- •14.Відношення міжмножинами.КругиЕйлера.Операції над множинами.Доповненняпідмножини.
- •17. Відношенння і їх властивості.
- •18.Відношення еквівалентності.Відношення порядку.
- •19. Поняття відповідності. Відповідність обернена даній.
- •20. Взаємооднозначні відповідності. Рівнопотужні відповідності.
- •21. Натуральні числа та їх властивості. Число нуль.
- •22.Додавання цілих невід'ємних чисел. Основні властивості додавання. Закони додавання.
- •23. Віднімання цілих невід'ємних чисел та його властивості.
- •24. Множина цілих невід'ємних чисел. Закони множення.
- •25.Ділення цілих невід’ємних чисел та його властивості.
- •26.Правила ділення суми на число і числа на добуток та їх властивості.
- •28.Множина невід'ємних чисел. Теоретико-множинний смисл кількісного натурального числа і нуля.
- •29. Смисл натурального числа і дій над числами - результатами виміру величин
- •30. Позиційні та непозиційні системи числення. Аксіоматика Пеаноє
- •31. Запис чисел в десятковій системі числення.
- •32. Виконання дій з многозначними (багатозначними) числами.
- •34. Ознаки подільності суми, різниці, добутку
- •35. Ознаки подільності в десятковій системі
- •36. Найбільший спільний дільник і найменше спільне кратне
- •37. Ознаки подільності на складені числа
- •38. Алгоритми Евкліда
- •39. Комбінаторика
- •40 Основні поняття теорії імовірностей
- •41. Об'єми многогранників та тіл обертання
- •42. Поверхня многогранників та тіл обертання
42. Поверхня многогранників та тіл обертання
Призма
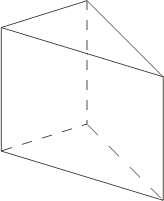
Площа
бічної поверхні довільної призми
дорівнює добутку периметра перпендикулярного
перерізу на бічне ребро:![]()
Площа
бічної поверхні прямої призми дорівнює
добутку периметра основи на висоту
призми:![]()
Паралелепіпед
Площа
бічної поверхні прямокутного паралелепіпеда
дорівнює добутку периметра основи на
висоту:![]()
Піраміда
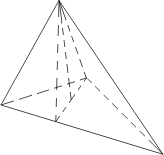
Площа бічної поверхні правильної піраміди дорівнює одній другій добутку периметра основи на апофему:
![]()
Площа бічної поверхні правильної зрізаної піраміди дорівнює добутку півсуми периметрів обох основ на апофему:
![]()
Циліндр
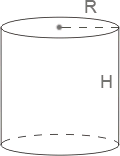
Площа
бічної поверхні циліндра обчислюється
за формулою:![]()
де R – радіус, а H – висота циліндра.
Конус
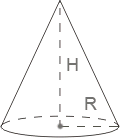
Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на твірну:
![]() де
l – твірна
де
l – твірна
Площа
зрізаного конуса дорівнює:![]()
Куля, сфера
Площа бічної поверхні кулі дорівнює почетвереній площі великого круга:
![]()
