39. Комбінаторика

Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку.

Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.

Комбінаторика пов'язана з багатьма іншими розділами математики. В основі розв’язування багатьох комбінаторних задач лежать два основних правила – правило суми і правило добутку. У комбінаториці розглядається вибір і розміщення елементів деякої скінченної множини на основі якихось умов. 

40 Основні поняття теорії імовірностей

Як і будь-яка інша математична теорія, теорій імовірності будується на основі деяких основі деяких основних понять, відношень та означень. За їх допомогою формуються основні правила, закони , теореми.

Дослід, експеримент,спостереження події називають випробуванням. Результат, наслідок, випробування називається подією.

Розрізняють події вірогідні, неможливі та випадкові.

Вірогідною називається подія, яка при випробуванні обов’язково наступає.

Неможливою називається така подія, яка в результаті випробування явно не відбувається.

Випадковою називається подія, яка в даному випробуванні може відбутися, а може і не відбутися.

Дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої одномуй тому самому випробуванні.

Дві події називаються несумісними, якщо поява однієї з них виключає появу другої в одному й тому самому випробуванні.

Дві події А і В називаються протилежними, якщо в даному випробуванні вони несумісні й одна з них обов’язково відбудеться.

Імовірність - числова характеристика можливості появи випадкової події за певної умови, яка може бути відтворена необмежену кількість раз.

Імовірністя випадкової події називається відношення кількості подій, які спираються цій події, до кількості всіх різноманітних несумісних подій , які утворюють повну групу подій під час певного випробування.

Д

41. Об'єми многогранників та тіл обертання

Об’єми многогранників

Об’єм будь-якої призми дорівнює добутку площі основи та висоти.

На рисунках наведені приклади призм із різними основами.

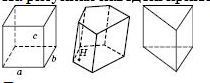
Для прямокутного паралелепіпеда отримаємо V=abc , де a, b, c — його виміри.

Для куба V=a² , де a — довжина ребра.

Для похилої призми (рисунок нижче зліва) об’єм можна обчислити як добуток площі перпендикулярного перерізу та довжини бічного ребра: V=Ql

Об’єм будь-якої піраміди (рисунок справа) дорівнює третині добутку площі її основи та висоти:

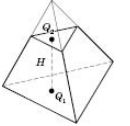
Об’єм зрізаної піраміди (див. рисунок) дорівнює , де H — висота, Q1 — площа нижньої основи, Q2 — площа верхньої основи.

Об’єми подібних тіл відносяться як куби їх відповідних лінійних розмірів. 

Об’єми круглих тіл

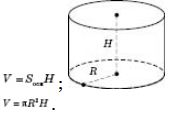
Об’єм циліндра (див. рисунок) дорівнює добутку площі його основи та висоти.

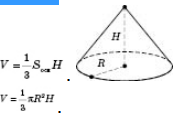
Об’єм конуса (див. рисунок) дорівнює одній третині добутку площі його основи та висоти.

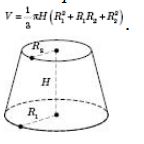
Об’єм зрізаного конуса (див. рисунок):

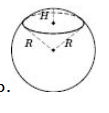
Об’єм кулі

На рисунку зображено кулю, кульовий сегмент і кульовий сектор.