Вопрос 36. Комплексная плоскость. Арифметические действия над комплексными числами. Комплексная плоскость

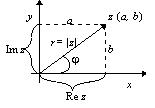  Рассмотрим декартову систему координат x0y. Пусть каждому числу z = a + bi ставится в соответствие точка z (a; b) . Такую плоскость назовем комплексной. Иными словами с каждой точ­кой z этой плоскости связывают радиус-вектор, определяющий положение данной точки. Угол между положительным направлением оси 0х и радиус-вектором, отсчитанным в направлении против часовой стрелки, называется аргументом.  Ось 0х на­зывается действительной осью комплексной плоскости.  Ось 0y называется мнимой осью комплексной плоскости.  Аргумент может принимать зна­чения из интервала -∞ < arg z < ∞. Наименьшее по модулю значение ар­гумента называется главным и обозначается arg z = φ .  Из рисунка следует, что:  ,  ,    Чтобы найти аргумент, необходимо учитывать, в какой четверти комплексной плоскос­ти находится число: 

 I квадрант φ1 = arg z1 = φ;

 II квадрант φ1 = arg z1 = π - φ;

 III квадрант φ1 = arg z1 = π + φ;

 IV квадрант φ1 = arg z1 = 2π - φ; .  Найдем модуль и аргумент комплексного числа :    так как z1 ∈ I квадранту.

Арифметические действия над комплексными числами

Сумма Суммой комплексных чисел z1 = a + bi и z2 = с + di называется комплексное число (a + c) + (b + d)i.  Таким образом:  z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i.  Сумма комплексных чисел обладает свойствами: 

 коммутативности: z1 + z2 = z2 + z1

 ассоциативности: (z1 + z2) + z3 = z1 + (z2 + z3) 

Произведение Произведением комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число (ac - bd)+(ad + bc)i. Определение произведения устанавливается с таким расчетом, чтобы (a + bi) и (c + di) можно было перемножить как алгебраические двучлены, считая при этом, что i*i = -1.  Произведение комплексных чисел обладает свойствами: 

 коммутативности: z1 * z2 = z2 * z1

 ассоциативности: (z1 * z2) * z3 = z1 * (z2 * z3)

 дистрибутивности: z1 * (z2 + z3) = z1 * z2 + z1 * z3  На основании определения произведения комплексных чисел можно определить натуральную степень комплексного числа: z(в степени n); = z * z * ... * z n раз. 

Разность Разностью комплексных чисел z1 = a + bi и z2 = c + di называется комп­лек­сное число z = z1 - z2 = (a - c) + (b - d)i. 

Частное Частным от деления комплексного числа z1 на комплексное число z2 на­зывается такое число z, которое удовлетворяет условию z? z2 = z2 ? z= = z1.

37 Тригометрическая и показательная формы комплексного числа

Комплексное число изображается на плоскости точкой или, эквивалентно, вектором с координатами (рис.1), и при таком способе задания операции сложения будет соответствовать векторное сложение. Плоскость называется комплексной плоскостью, ось - действительной осью и - мнимой осью.

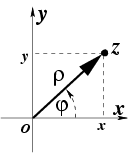
Рис.1. В полярной системе координат на комплексной плоскости число будет определяться парой действительных чисел (рис.1). Из уравнений, связывающих декартовую и полярную системы координат, следует:

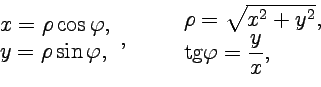(8)

и имеет смысл модуля , а называется аргументом числа , . С использованием (8) число запишется как

(9)

и называется тригонометрической формой записи комлексного числа . Отметим, что аргумент определен с точностью до целого кратного , что записывается как

(10)

Выражение в скобках формулы (9) может быть преобразовано с помощью соотношения:

(11)

которое называется формулой Эйлера и позволяет получить еще один способ записи комплексных чисел

(12)

Выражение (12) называется показательной формой записи комплексного числа и является одной из наиболее часто встречающихся в комплексном анализе. Использование символа экспоненты в (11) указывает на то, что эта величина должна обладать и теми же свойствами.