41 Однородные дифференциальные уравнения первого порядка

Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид

(7)

Подстановка ; , где преобразует это уравнение к уравнению с разделяющимися переменными.

,

,

Замечание. Функция называется однородной степени , если , где - некоторая константа. Например, функция является однородной функцией степени два, поскольку

А функция является однородной функцией нулевой степени однородности, так как

.

Поэтому общий вид однородного дифференциального уравнения часто записывают как

,

где - однородная функция нулевой степени однородности.

ТЕОРЕМА.(теорема Коши). Если функция f(х,y) и ее частная производная f'y(х,y) определены и непрерывны в некоторой области G плоскости Оху, то какова бы ни была внутренняя точка (x0,y0) области G, в некоторой окрестности этой точки существует единственное решение уравнения у'=f(x,у), удовлетворяющее условиям: у =у0 при х =х0 (6)

42. Первого порядка.

Уравнение вида

F(x, y, y^/) = 0 (1.4)

называется уравнением первого порядка.

В простейших случаях оно может быть разрешено относительно

у^/=f(x,y). (1.4’)

Общее решение (1.4) имеет вид

у=j(х,С), (1.5)

где С - константа.

Геометрически общее решение представляет собой семейство интегральных кривых.

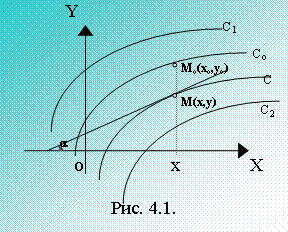
Интегральные кривые обладают тем свойством, что все касательные в точке М(х,у) имеют наклон tga = f ’(x,y).

Если задать точку М₀(х₀,у₀), через которую должна проходить интегральная кривая, то это требование называется начальным условием

y = у₀, х = х₀ и тогда

у₀ = j(х₀,С₀).

Определяется С - константа; в результате получаем частное интегральное решение у = j(х,С₀).

В этом состоит задача Коши.

Задача Коши. Найти решение у = j(х) дифференциального уравнения (1.4’), удовлетворяющее начальному условию: у₀=j(х₀)

. З а м е ч а н и е. Нет общего метода интегрирования уравнения первого порядка. Обычно рассматривают некоторые отдельные типы таких уравнений, для каждого из которых дается свой способ.

43 Однородные дифференциальные уравнения второго порядка

Уравнение второго порядка

Однородное уравнение второго порядка:

a2y'' + a1y' + a0y = 0

интегрируется следующим образом:

Пусть λ1,λ2 — корни характеристического уравнения.

a2λ2 + a1λ + a0 = 0,

являющегося квадратным уравнением.

Вид общего решения однородного уравнения зависит от значения дискриминанта :

при Δ > 0 уравнение имеет два различных вещественных корня

Общее решение имеет вид:

при Δ = 0 — два совпадающих вещественных корня

Общее решение имеет вид:

y(t) = c1e^αt + c2te^αt

при Δ < 0 существуют два комплексно сопряженных корня

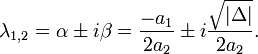
Общее решение имеет вид:

y(t) = c1e^αt cos(βt) + c2e^αt sin(βt)