
- •1. Огляд історії теорії оптимізації.
- •§2 Способы решения задач на экстремумы
- •2. Деякі старовинні екстремальні задачі.
- •3. Основні етапи розв’язування екстремальних задач.
- •4. Постановка задачі оптимізації та основні поняття.
- •Основні типи задач оптимізації.
- •6. Задача нелінійного програмування (знлп), загальна форма.
- •7. Геометрична інтерпретація задачі нелінійного програмування.
- •8. Приклади екстремальних задач та їх формалізація.
- •9,10. Необхідні і достатні умови одновимірної оптимізації.
- •11. Класифікація методів оптимізації. Классификация методов оптимизации
- •12. Теорема Вейєршрасса.
- •13.Классические методы поиска экстремума функции одной переменной.
- •14. Класичний метод знаходження екстремумів функції однієї змінної.
- •16. Метод знаходження екстремумів функції багатьох змінних: виключення частини змінних Якобі.
- •17. Метод множителей Лагранжа.
- •18 . Опуклі множини та їх властивості.
- •Властивості опуклих множин
- •19. Опуклі функції та їх основні властивості.
- •Властивості опуклих функцій
- •20. Методи оптимізації диференційованих функцій
- •21. Необхідні умови мінімуму в задачах оптимізації.
- •22. Теорема Куна-Таккера.
- •Необхідні умови
- •Умови регулярності
- •Достатні умови
- •23. Двоїстість в задачі опуклого програмування. Приклади.
- •24. Наближені чисельні методи оптимізації.
- •25. Метод деления пополам Метод деления пополам
- •26. Метод золотого сечения
- •27. Метод касательних.
- •Обоснование
- •Алгоритм
- •28. Метод парабол.
- •29. Пошук глобального мінімуму функції однієї змінної в середовище Excel.
- •30. Покоординатний спуск. Введение
- •Метод покоординатного спуска Алгоритм
- •Критерий останова
- •Сходимость метода
- •Числовые примеры
- •31,32. Градієнтні методи.
- •33. Чисельні методи багатовимірної оптимізації: метод Ньютона та його модифікації.
- •34. Чисельні методи багатовимірної оптимізації: методи спряжених напрямів.
- •35. Чисельні методи багатовимірної оптимізації: методи спряжених напрямів.
19. Опуклі функції та їх основні властивості.
Опукла функція — функція, яка визначена на опуклій множині лінійного простору, і задовольняє нерівності
![]()
при всіх λ ∈ [0, 1].
Нехай область визначення опуклої функції f(x) лежить в скінченовимірному просторі, тоді f(x) неперервна в будь якій внутрішній точці цієї області.
Властивості опуклих функцій
Нехай x1, ..., xm — будь які точки із області визначення опуклої функції f(x), λ1, ..., λm — невід'ємні числа, які в сумі дорівнюють 1. Тоді
 .
.
Якщо f(x) — двічі неперервно-диференційована опукла функція, то матриця її других похідних напівдодатньо визначена.
20. Методи оптимізації диференційованих функцій
Градієнтні методи
Задача
1. Знайти
![]() для заданої функції
для заданої функції
![]() .
.
Припущення
1. Функція
![]() диференційована в
диференційована в
![]() .
.
В
градієнтних методах мінімізації за
напрямок руху в
![]() -й
ітерації обирається вектор, протилежний
градієнту функції
в точці
-й
ітерації обирається вектор, протилежний
градієнту функції
в точці
![]() .
Різні варіанти градієнтного методу
відрізняються один від одного способом
вибору крокового множника в
-й
ітерації, а також тими чи іншими способами
(різницевої) апроксимації градієнтів.
.
Різні варіанти градієнтного методу
відрізняються один від одного способом
вибору крокового множника в
-й
ітерації, а також тими чи іншими способами
(різницевої) апроксимації градієнтів.
21. Необхідні умови мінімуму в задачах оптимізації.
Теорема.1. Якщо
диференційована функція
![]() має
в точці
має
в точці
![]() екстремум,
то
екстремум,
то
![]() .
.
Теорема 2. У точці екстремуму функції кількох змінних кожна її частинна похідна першого порядку або дорівнює нулю, або не існує.
Означення. Точки, в яких частинні похідні першого порядку деякі функції дорівнюють нулю або не існують, називаються критичними точками.
Достатні умови існування екстремуму.
Теорема. Нехай
є
критична точка функції
,
яка в цій точці є неперервною, і нехай
існує окіл точки
![]() ,
в якому
має
похідну
,
в якому
має
похідну
![]() ,
крім, можливо, точка
.
Тоді:
,
крім, можливо, точка
.
Тоді:
1) якщо в інтервалі
![]() похідна
похідна
![]() ,
а в інтервалі
,
а в інтервалі
![]() похідна
похідна
![]() ,
то
є
точкою максимуму функції
;
,
то
є
точкою максимуму функції
;
2) якщо в інтервалі
![]() ,
а в інтервалі
,
а в інтервалі
![]() то
є
точкою мінімуму функції
;
то
є
точкою мінімуму функції
;
3) якщо в обох
інтервалах
![]() і
і
![]() похідна
похідна
![]() має
той самий знак ( набуває або тільки
додатних, або тільки від’ємних значень),
то
не
є екстремальною точкою функції
.
має
той самий знак ( набуває або тільки
додатних, або тільки від’ємних значень),
то
не
є екстремальною точкою функції
.
22. Теорема Куна-Таккера.
В математиці, умови Каруша — Куна — Такера — необхідні умови оптимальності розв'язку задачі нелінійного програмування, при виконанні деяких умов регулярності. Нехай маємо наступну задачу оптимізації:
![]()
при виконанні умов
![]()
де
![]() —
функція,
що мінімізується,
—
функція,
що мінімізується,
![]() —
функції обмежень-нерівностей
і
—
функції обмежень-нерівностей
і
![]() —
функції обмежень-рівностей.
—
функції обмежень-рівностей.
Необхідні умови
Припустимо, що
задана функція мети (функція значення
якої слід мінімізувати)
![]() і
обмежуючі функції
і
обмежуючі функції
![]() і
і
![]() .
.
Позначимо
![]() підмножину
підмножину
![]() для
елементів якої в обмеженнях-нерівностях
виконується рівність
для
елементів якої в обмеженнях-нерівностях
виконується рівність
![]() Припустимо,
що дані функції є неперервно
диференційованими
в точці
Припустимо,
що дані функції є неперервно
диференційованими
в точці
![]() .
Якщо
є
локальним
мінімумом, що задовольняє
деякі умови регулярності, то існують
константи,
.
Якщо
є
локальним
мінімумом, що задовольняє
деякі умови регулярності, то існують
константи,
![]() і
і
![]() такі
що виконуються властивості:
такі
що виконуються властивості:
Стаціонарність

Допустимість
![]()
![]()
Двоїста допустимість
![]()
Спряженість
![]()
Умови регулярності
Найпоширенішою умовою регулярності є умова лінійної незалежності градієнтів:
якщо для локального
мінімуму
вектори
![]() —
лінійно
незалежні, то в точці
виконуються
умови Каруша — Куна — Такера.
—
лінійно
незалежні, то в точці
виконуються
умови Каруша — Куна — Такера.
Умови Мангасар'яна — Фромовіца. Якщо для локального мінімуму існує вектор
 для
якого:
для
якого:
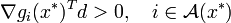
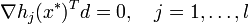
Вектори
 —
лінійно незалежні,
—
лінійно незалежні,
то в точці виконуються умови Каруша — Куна — Такера.
