35. Чисельні методи багатовимірної оптимізації: методи спряжених напрямів.

Минимизация по правильному симплексу.

Правильным симплексом в пространстве En называется множество из n+1 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса.

В пространстве E2 правильным симплексом является совокупность вершин равностороннего треугольника, а в E3 - правильного тетраэдра. Если x0 - одна из вершин правильного симплекса в En, то координаты остальных n вершин x1,..., xn можно найти, например, по формулам:

	xj0 + d1 , i != j,
xji ={	(1)
	xj0 + d2 , i=j,

где d1 = a(sqrt(n+1) - 1) / n*sqrt(2), d2 = a(sqrt(n+1) + n - 1) / n*sqrt(2), a - длина ребра.

Вершину x0 симплекса, построенного по формулам (1), будем называть базовой. В алгоритме симплексного метода используется следующее важное свойство правильного симплекса. По известному симплексу можно построить новый симплекс путем отражения какой-либо вершины, например, xk симметрично относительно центра тяжести xc остальных вершин симплекса. Новая и старая вершины y и xk связаны соотношением: (y+ xk)/2 = xс, где xc = (1/n)Sum(xi) для всех i!=k. В результате получаем новый симплекс с тем же ребром и вершинами y=2xс-xk, xi, i=0,...,n, i!=k. Таким образом происходит перемещение симплекса в пространстве. На рисисунке представлена иллюстрация этого свойства симплекса для двумерной области.

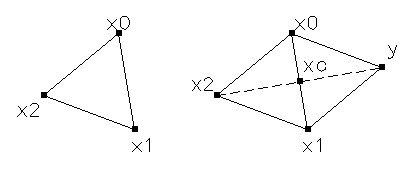
Построение нового симплекса в Е2 отражением точки х2.

Поиск точки минимума функции f(x) с помощью правильных симплексов производится следующим образом. На каждой итерации сравниваются значения функции в вершинах симплекса. Затем проводится описанная выше процедура отражения для той вершины, в которой f(x) принимает наибольшее значение. Если в отраженной вершине получается меньшее значение функции, то переходят к новому симплексу. Если же попытка отражения не приводит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину x0 старого симплекса, в которой функция принимет минимальное значение. Поиск точки минимума f(x) заканчивают, когда либо ребро симплекса, либо разность между значениями функции в вершинах симплекса становятся достаточно малыми.

 

Алгоритм минимизации по правильному симплексу.

Начальный этап. Выбрать параметр точности eps, базовую точку x0, ребро a и построить начальный симплекс по формулам (1). Вычислить f(x0).

 

Основной этап.

Шаг 1. Вычислить значения f(x) в вершинах симплекса x1,..., xn.

Шаг 2. Упорядочить вершины симплекса x0,..., xn так, чтобы f(x0)<=f(x1)<=...<=f(x[n-1])<=f(xn).

Шаг 3. Проверить условие (1/n)Sum[f(xi)-f(x0)]^2 < eps^2, i=[1,n].

Это одно из возможных условий останова. При его выполнении "дисперсия" значений f(x) в вершинах симплекса становится меньше e2, что, как правило, соответствует либо малому ребру a симплекса, либо попаданию точки минимума x* внутрь симплекса, либо тому и другому одновременно.

Если это условие выполнено, то вычисления прекратить, полагая x*= x0. В противном случае перейти к шагу 4.

Шаг 4. Найти xс и выполнить отражение вершины xn : y=2*xс- xn. Если f(y)<f(xn), то положить xn=y и перейти к шагу 2. Иначе - перейти к шагу 5.

Шаг 5. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной x0. Остальные n вершин симплеска найти по формуле xi=( xi+ x0)/2, i=1,...,n. Перейти к шагу 1.