Содержание

Введение 7

1 Теоретическая часть 8

1.1 Первичная обработка статистических данных. 8

1.1.1 Упорядочение данных наблюдения 8

1.1.2 Способ равных интервалов 8

1.1.3 Способ равных частот 9

1.1.4 Группировка данных наблюдения над дискретной случайной величиной 10

1.1.5 Эмпирическая функция распределения 11

1.1.6 Эмпирическая плотность вероятности 11

1.1.7 Эмпирический ряд распределения 12

1.1.8 Статистическая процедура «Описательная статистика» 12

1.2 Порядковые статистики и ранги 14

1.2.1 Статистическая процедура “Ранг и персентиль” 14

1.2.2 Функция РАНГ 15

1.3 Проверка параметрических гипотез 15

1.3.1 Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий) 15

1.3.2 Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий) 16

1.3.3 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z- критерий) 17

1.3.4 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t- критерий, равные дисперсии) 17

1.3.5 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t- критерий, различные дисперсии) 18

1.3.6 Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (F-критерий) 19

1.3.7 Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена) 19

1.4 Проверка гипотезы о законе распределения случайной величины (критерии согласия) 21

1.4.1 Критерий Крамера-Мизеса-Смирнова 21

1.4.2 Критерий Андерсона-Дарлинга 21

1.4.3 Критерии W Шапиро-Уилка 21

1.4.4 Критерий согласия хи-квадрат Пирсона 22

1.4.5 Критерий согласия Колмогорова 22

2 Практическая часть 23

2.1 Исходные данные 23

2.1.1 Упорядочение данных наблюдения 24

2.1.2 Способ равных интервалов 25

2.1.3 Способ равных частот 26

2.1.4 Группировка данных наблюдения над дискретной случайной величиной 27

2.1.5 Эмпирическая функция распределения 28

2.1.6 Эмпирическая плотность вероятности 29

2.1.7 Эмпирический ряд распределения 30

2.1.8 Статистическая процедура «Описательная статистика» 31

2.2 Порядковые статистики и ранги 32

2.2.1 Статистическая процедура “Ранг и персентиль” 32

2.2.2 Функция РАНГ 32

2.3 Проверка параметрических гипотез 33

2.3.1 Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий) 33

2.3.2 Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий) 34

2.3.3 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z- критерий) 35

2.3.4 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t- критерий, равные дисперсии) 36

2.3.5 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t- критерий, различные дисперсии) 37

2.3.6 Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (F-критерий) 37

2.3.7 Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена) 40

2.4 Проверка гипотезы о законе распределения случайной величины (критерии согласия) 43

2.4.1 Критерий Крамера-Мизеса-Смирнова 43

2.4.2 Критерий Андерсона-Дарлинга 44

2.4.3 Критерии W Шапиро-Уилка 45

2.4.4 Критерий согласия хи-квадрат Пирсона 48

2.4.5 Критерий согласия Колмогорова 49

Заключение 51

Список литературы 52

Приложение А 7

Введение

Текст содержания введения.

1Теоретическая часть

1.1Первичная обработка статистических данных.

Любое статистическое исследование начинается со сбора данных об исследуемом случайном объекте. Таким объектом может быть случайное событие, случайная величина, система случайных величин (случайный вектор) или случайная функция. Этот этап работы принято называть наблюдением. Данные, собранные и зафиксированные в ходе наблюдения, называются данными наблюдения.

В данной курсовой работе рассматриваются данные о выборах в Государственную Думу Российской Федерации 2011 года.

1.1.1Упорядочение данных наблюдения

Наблюденные значения исследуемой случайной величины в статистике принято рассматривать как случайную выборку из бесконечной генеральной совокупности реализаций этой случайной величины, которые могли бы быть получены при проведении всех мыслимых наблюдений над этой случайной величиной. При этом числа образующие выборку, называют элементами выборки, а число n этих элементов – объемом выборки. Выборка является основным исходным объектом любого статистического исследования.

Упорядочение данных наблюдения по возрастанию выполняется по следующему условию:

, (1)

где – наблюдаемая величина; – количество элементов выборки.

1.1.2Способ равных интервалов

Группировка данных наблюдения способом равных частот осуществляется следующим образом:

1. Определяют число k интервалов группировки и длину ∆х интервала группировки.

2. Задаются «подходящим» значением x’0 левой границы первого интервала группировки.

3. С помощью формулы x’i = x’i-1 + ∆х, i =1, 2, …, k, вычисляют границы интервалов группировки.

4. Подсчитывают групповые частоты n1, n2, …, nk попадания данных наблюдения в каждый из интервалов группировки.

5. Составляют итоговую таблицу результатов группировки – таблицу частот.

Число интервалов группировки является целым числом и в Excel определяется по следующей формуле:

(2)

Граница интервала группировки ищется по следующей формуле:

(3)

где длина интервала группировки

1.1.3Способ равных частот

Группировка данных наблюдения по равным интервалам имеет существенный недостаток – при определении числа k интервалов группировки и длинны ∆х этих интервалов учитывается только объем n выборки и ее размах Wn = x(n) - x(1) и совершенно не учитываются особенности распределения данных наблюдения. От этого недостатка свободен способ группировки, называемый способом равных частот. Этот способ может быть использован только при наличии предварительного упорядоченных данных наблюдения.

Для начала ищем ориентировочное число интервалов по следующей формуле:

(4)

Ориентировочное число данных наблюдения вычисляем по формуле (5):

(5)

Границы интервалов вычисляют по формуле:

(6)

при условии

где - длина интервала группировки

1.1.4Группировка данных наблюдения над дискретной случайной величиной

Содержание процесса группировки данных наблюдения над дискретной случайной величиной зависит от числа l различных возможных значений этой случайной величины. Для группировки данных наблюдения над дискретной случайной величиной с малым числом l возможных значений в Excel используют рассмотренные ранее средства – процедуру Гистограмма и встроенную статистическую функцию ЧАСТОТА. Различие заключается в том, что в поле Интервал карманов вводятся не границы xi’ интервалов группировки, а все целые числа от xmin =x(1) до xmax = x(n) включительно.

1.1.5Эмпирическая функция распределения

Эмпирическим аналогом функции распределения F(x) является эмпирическая функция распределения Fn*(x), которая при каждом x принимает значение, равное относительной частоте Pn*(X<x) случайного события X<x.

Эмпирическая функция распределения при большом числе n наблюдений определяется по формуле:

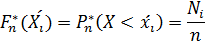
(7)

где – накопленная частота - го интервала группировки

1.1.6Эмпирическая плотность вероятности

Значение эмпирической плотности вероятности в -м интервале группировки определяется с помощью формулы:

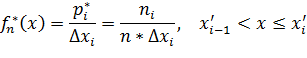
(8)

где – относительная частота (частность) попадания элементов выборки в -й интервал группировки

– длина интервала

1.1.7Эмпирический ряд распределения

1.1.8Статистическая процедура «Описательная статистика»

Для характеристики отдельных свойств распределения данных наблюдения в математической статистике широко используют специальные числовые параметры, найденные по результатам наблюдения и отражающие в сжатом виде основные, существенные черты распределения выборочных данных. Эти числовые параметры называют эмпирическими числовыми характеристиками. Выборочной характеристикой положения называется найденный по выборке числовой параметр, определяющий положения центра распределения наблюденных значений исследуемой случайной величины. Ниже приведены числовые характеристики.

Выборочное среднее вычисляют по формуле:

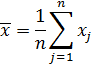(9)

Выборочную медиану вычисляют по формуле:

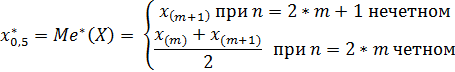(10)

Выборочную моду вычисляют по формуле:

(11)

где - границы модального интервала

- значения эмпирической функции плотности в интервале, предшествующем модальному, модальному и следующим за модальным соответственно

Выборочную дисперсию вычисляют по следующей формуле:

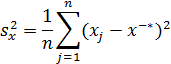(12)

Выборочное отклонение вычисляют по следующей формуле:

(13)

Выборочный центральный момент вычисляют по формуле:

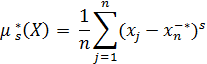
(14)

где – порядок

Выборочный коэффициент асимметрии вычисляют по формуле:

(15)

Выборочный коэффициент эксцесса вычисляют по формуле

(16)