4 Комплексний евклідовий простір (унітарний простір)

Лінійний простір над полем комплексних чисел називається комплексним евклідовим простором або унітарним, якщо в нім визначена операція скалярного добутку двох будь-яких векторів, тобто вказано правило, по якому кожній парі векторів і простору ставиться в відповідність комплексне число , при цьому виконуються наступні умови (аксіоми скалярного добутку)

1. ;

2. ;

3. ;

4. , Лише при .

Тут – довільне комплексне число, – число, спряжене числу , – дійсне число.

Властивості скалярного добутку:

1. ;

2. .

Комплексний евклідовий простір можна зробити нормованим, якщо кожному вектору поставити у відповідість дійсне число . Превірка аксіом норми здійснюється так само, як і в дійсному евклідовому просторі. Вона основана на використанні нерівності Коші – Буняковсякого для унітарного простору .

В унітарному просторі поняття кута між двома векторами не використовується, але два вектори і таких, що , називаються ортогональними.

В комплексному евклідовому просторі існують ортонормовані базиси. Процесс ортогоналізції довільного базису унітарного простору співпадає з процессом ортогоналізації базиса дійсного евклідового простору.

Нехай – ортонормований базис комплесного евклідового простору, а і – два довільно взятих вектори цього простору. Тоді на основі аксіом і властивостей скалярного добутку

де – числа, спряжені комплексним числам . Таким чином , тобто скалярний добуток двох векторів унітарного простору, в якому вибраний ортонормований базис, рівний сумі добутків координат першого вектору на відповідні спряжені значення координат іншого вектору.

5 Приклади розв’язання задач

1. Застосовуючи процес ортогоналізації, побудуйте ортогональний базис підпростору, натягнутого на дану систему векторів: , , .

Розв’язання:

~ ~ ~ .

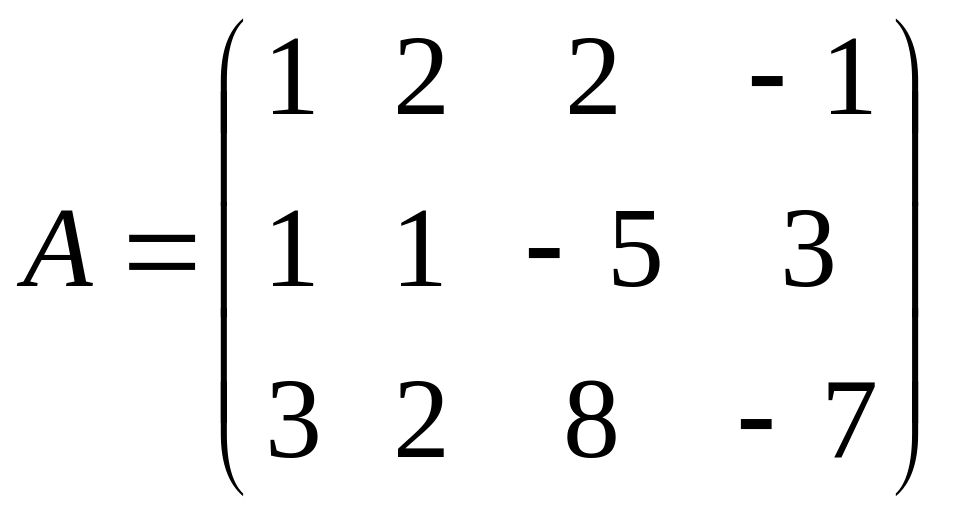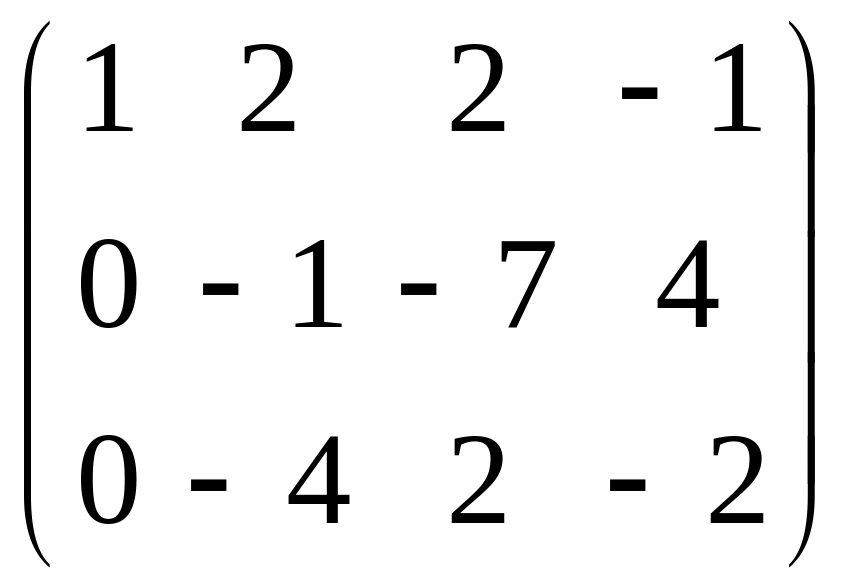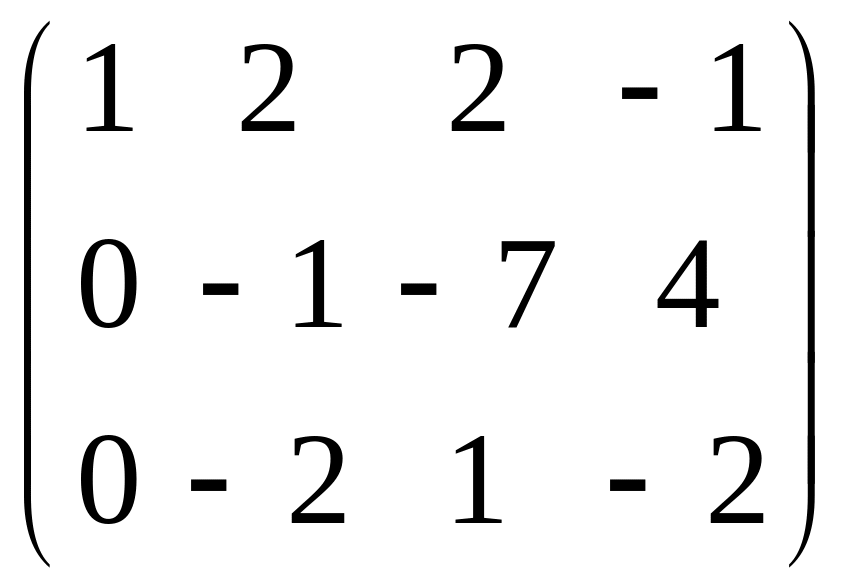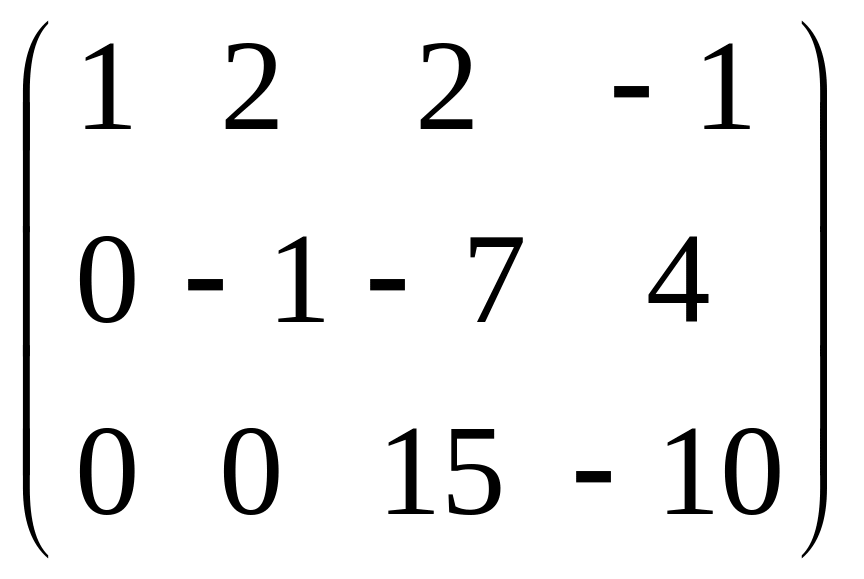, – кількість векторів, 3= вектори лінійно незалежні

Нехай , тоді .

Провіримо ортогональність:

;

;

;

; ; ;

;

;

;

.

2. Знайдіть ортогональну проекцію і ортогональну складову вектора на лінійний простір = .

Розв’язання:

~ ~ =

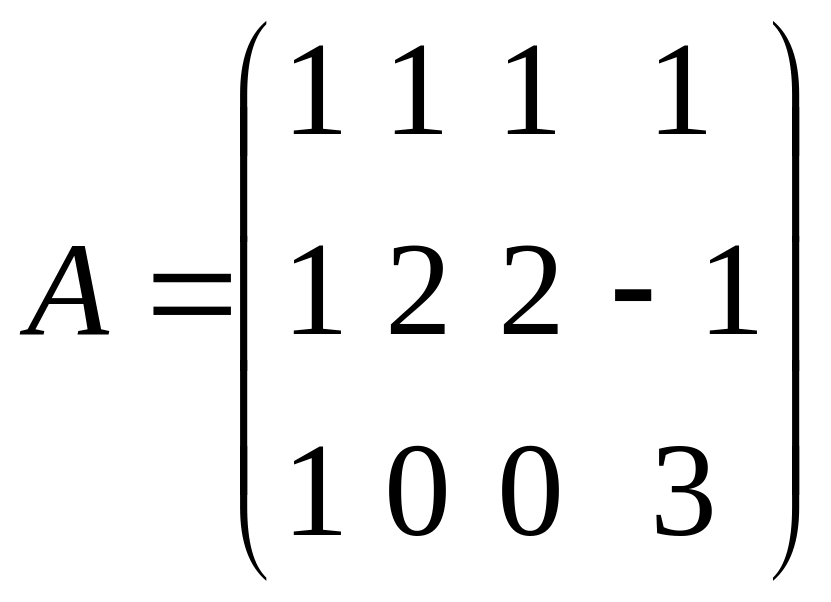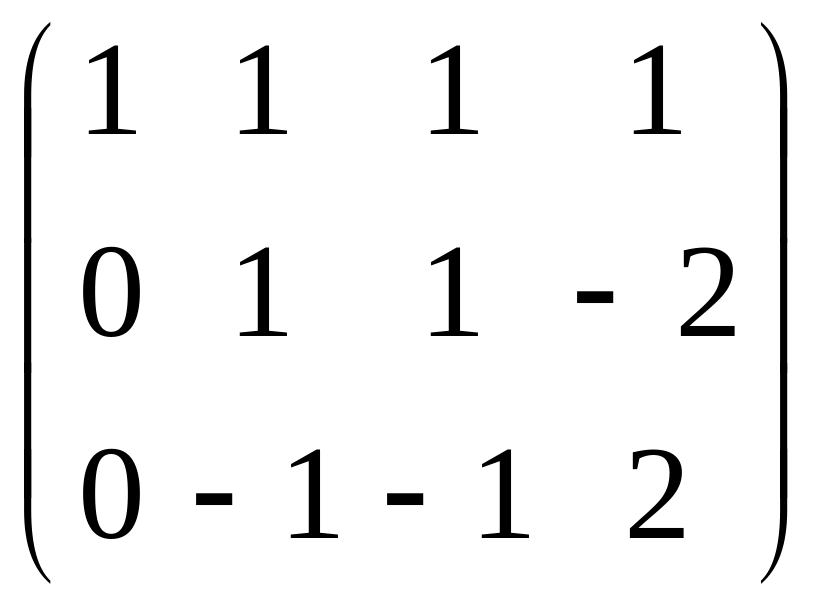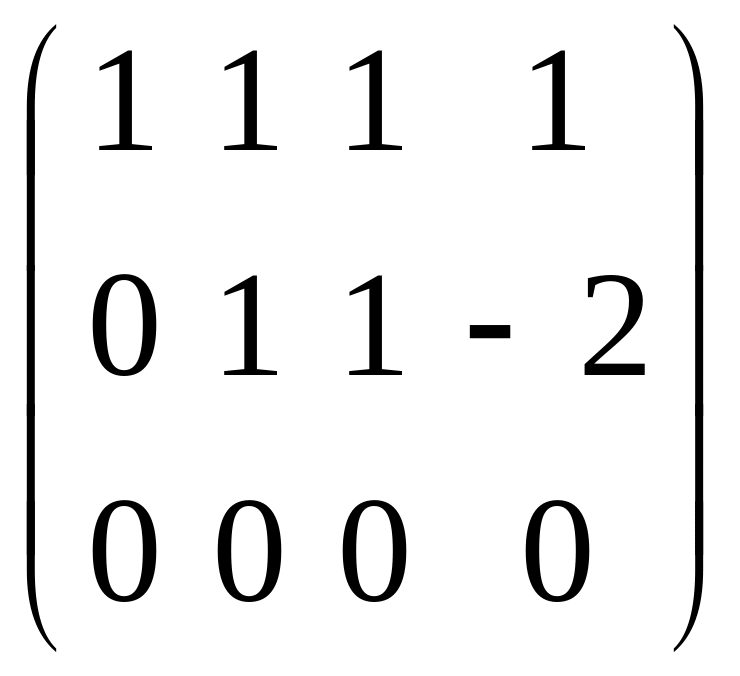Будемо шукати ортогональну проекцію вектора на у вигляді:

Так як – ортогональна складова, то = + =

Оскільки :

3. Знайти базис ортогонального доповнення підпростору , натягнутого на вектори , ,

Розв’язання

Складаємо матрицю, для перевірки лінійної залежності векторів

Rang A = 2

Запишемо вектор

Провіряємо ортогональність і

Знайдемо фундаментальну систему рішень

Запишемо систему

Виражаємо змінні

Складаємо таблицю

	-1	1	0
-1	-1	0	1

Із таблиці слідує, що і . Отже, .

4. Доведіть, що .

Розв’язання:

Для того, щоб довести нерівність необхідно перевірити аксіоми скалярного добутку.

аксіома виконується, так як скалярний добуток являється дійсним

. Аксіома тотожності виконується.

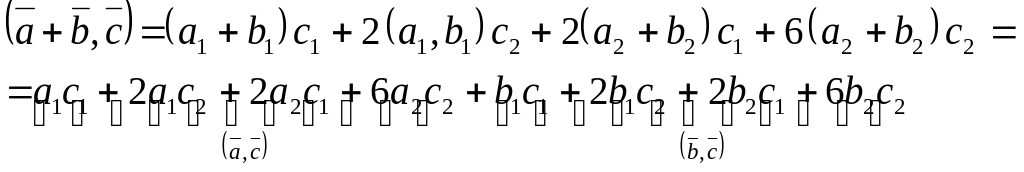
Аксіоми скалярного добутку виконуються.

5. Нехай дано два вектори . Знайдіть довжини векторів , якщо

А) задано

Розв’язання:

Довжина вектора визначається за формулою .

Знайдемо

Б)

Обчислимо

6. Знайдіть норму вектора .

Розв’язання:

Для того, щоб знормувати вектор, потрібно знайти його довжину , а потім використати формулу