1 Дійсний евклідовий простір

Лінійний простір над полем дійсних чисел називається дійсним евклідовим простором, якщо в ньому визначена операція скалярного добутку двох будь-яких векторів, тобто будь-якій парі векторів і простору ставиться у відповідність дійсне число . При цьому для будь-яких векторів простору повинні виконуватися умови (аксіоми).

1. =

2.

3. , – число

4., лише при .

Розглянемо приклади евклідових просторів.

1. Векторний простір направлених відрізків над полем дійсних чисел, в якому введений таким чином скалярний добуток двох довільних векторів і

= , , ( – кут між і ),

=0, якщо = або = ,

є дійсним евклідовим простором, оскільки виконуються всі аксіоми скалярного добутку.

2. Нехай С – множина всіх неперервних на відрізку дійсних функцій. Ця множина є лінійним простором над полем дійсних чисел. Простір стане евклідовим, якщо кожній парі функцій і із множини С поставити у відповідність число

=.

Всі вимоги, що пред'являються до скалярного добутку, виконуються.

Теорема 1.1. Для будь-яких двох векторів і дійсного евклідового простору (нерівність Коші-Буняковского).

Лінійний простір називається нормованим, якщо кожному вектору цього простору поставлено у відповідність число , яке називається нормою вектору або його довжиною. При цьому повинні виконуватися умови (аксіоми норми)

1. , причому , лише коли ;

2. – нерівність трикутника;

3. для любого числа .

Всякий евклідовий простір можна вважати нормованим, якщо кожному вектору простору поставити у відповідність число . Щоб переконатися в цьому, потрібно перевірити виконання всіх аксіом норми. Перша і третя аксіоми норми виконуються, оскільки по першій властивості скалярного добутку , причому лише при , тобто , лише коли , а по третій властивості , тобто . Аксіома трикутника також виконується. Дійсно, . Згідно нерівності Коші – Буняковского . Отже, .

По аналогії з випадком тривимірного простору направлених відрізків введемо поняття кута між двома векторами евклідового простору. Під кутом між яким – небудь ненульовими векторами і простору розуміється таке число , що , , .

Це визначення коректне, оскільки згідно з нерівністю Коші – Буняковского , тому дріб, що визначає значення по модулю менше одиниці. Отже, які б не були ненульові вектори і евклідового простору, існує єдине число , що визначає кут між векторами і .

Приклад. Нехай – евклідовий простір, елементами якого є дійсні функції, неперервні на відрізку . Скалярний добуток двох довільних елементів и простору визначимо відомим способом .

Потрібно знайти кут між елементами и .

Розв’язання:

Згідно з визначенням скалярного добутку .

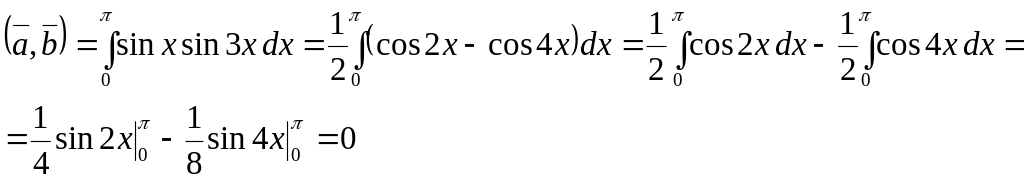
На основі формули , , , отже, кут між елементами і простору дорівнює .

Два вектори і евклідового простору називаються ортогональними, якщо їх скалярний добуток . Суму + двох ортогональних векторів і називатимемо гіпотенузою прямокутного трикутника і .

Теорема Піфагора. Квадрат довжини гіпотенузи прямокутного трикутника дорівнює сумі квадратів довжин катетів.