15. Інтеграл лебега від невід’ємної необмеженої вимірної функції. Сумовні функції довільного знаку.

Інтеграл Лебега від невід’ємної необмеженої вимірної функції

Узагальнимо поняття інтегралу Лебега на необмежені вимірні функції. Спочатку розглянемо невід’ємні функції. Нехай функція - вимірна і невід’ємна на вимірній множині 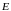, а - деяке число.

Введемо функцію:

.

Ця функція вимірна на , оскільки для вимірною буде множина:

.

Розглянемо послідовність функцій:

Кожна з них обмежена і вимірна на , а отже інтегрована на за Лебегом. Оскільки

для , то

і існує скінчена або нескінчена границя

.

Означення 1. Границя називається інтегралом Лебега функції на множині і позначається . Якщо ця границя скінчена, то функція називається інтегровною або сумовною на множині .

Інтеграл визначається для будь-якої невід’ємної вимірної функції, але сумовною будемо називати лишу ту, для якої інтеграл скінчений. Очевидно, що для обмеженої вимірної і невід’ємної функції нове означення співпадає з даним раніше, оскільки для досить великих , де .

Властивості інтеграла Лебега від невід’ємної вимірної функції.

1. Якщо - сумовна на множині , то вона майже скрізь обмежена на цій множині.

Доведення

Дійсно, нехай - множина тих точок із множини , де функція необмежена. На множині функція . Оскільки , то:

.

Якби , тобто , то зростав би необмежено разом з , що суперечило б сумовності функції . Отже, , тобто - майже скрізь обмежена.

2. Якщо , то будь-яка невід’ємна функція - сумовна на і

.

3. Якщо на множині , то .

4. Якщо - невід’ємна і вимірна функція на , а і - вимірна підмножина, то: .

5. Якщо функції та - невід’ємні і вимірні на , причому , то

.

6. Якщо та - невід’ємні і вимірні функції, задані на , то

.

7. Якщо - невід’ємна і вимірна функція на , а число , то:

.

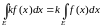8. Нехай - об’єднання скінченної або зчисленної кількості вимірних множин, які попарно не перетинаються: . Для всякої невід’ємної вимірної функції , заданої на множині , має місце:

.

Сумовні функції довільного знаку

Розширимо означення інтеграла Лебега на необмежені функції довільного знака. Нехай - вимірна функція на вимірній множині . Введемо функції та , поклавши:

.

Ці функції вимірні та невід’ємні, тому існують інтеграли:

та

Зрозуміло, що .

Означення 2.

Якщо хоча б одна із функцій або сумована на , то скінчена чи нескінчена різниця:

-

називається інтегралом Лебега функції на множині і позначається .

Означення 3.

Функція називається сумовною (інтегровною) на , якщо інтеграл існує і є скінченним.

Очевидно, будь-яка вимірна обмежена функція сумовна і нове означення співпадає з даним раніше.

Теорема

Для того, щоб вимірна функція була сумовною на необхідно і достатньо, щоб сумовною на була функція . Якщо дана умова виконується, то:

.

Доведення

Оскільки , то за властивістю 6 маємо:

,

а, отже

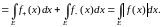
Теорему доведено.

Властивості 1-8 переносяться і на сумовні функції довільного знаку.