
- •Еквівалентність множини. Потужність множини. Порівняння потужностей.
- •Зчисленні множини та їх властивості
- •Незчисленність множини дійсних чисел [0;1]. Множини потужності континууму.
- •4.Граничні точки множини. Замкнені множини, властивості замкнених множин.
- •5. Відкриті множини, властивості відкритих множин.
- •6. Структура відкритих, замкнених підмножин множини дійсних чисел.
- •7. Множина Кантора, підмножини р0 і g0, та їх властивості.
- •8. Задача вимірювання множин. Зовнішня і внутрішня міри Лебега та їх властивості.
- •13. Основні властивості інтеграла лебега. Зв'язок інтеграла рімана з інтегралом лебега
- •14. Збіжність майже скрізь і зюіжність за мірою. Граничний перехід під знаком інтеграла лебега
- •15. Інтеграл лебега від невід’ємної необмеженої вимірної функції. Сумовні функції довільного знаку.
6. Структура відкритих, замкнених підмножин множини дійсних чисел.
Е⊂R, Е≠R, тобто Е – лінійна множина відмінна від усієї числової прямої.
Нехай Е – замкнена. Можна довести, що обмежена знизу замкнена множина має най лівішу точку. ∃ а∊ Е, що ∀ х ∊Е: а≤ х. Аналогічно: замкнена обмежена зверху множина має най правішу точку. ∃ b ∊E ∀ x ∊ E: x≤ b.
Отже, якщо замкнена множина є обмежена, то Е⊂[a;b], a∊E, b∊E, а інтервали (-∞;а) і (b;+∞) не містять точок множини Е.
ОЗН: Інтервал, кінці якого належать множині Е і який не містить точок множини Е називають суміжним інтервалом до замкненої множини Е. (-∞;а) і (b;+∞) – теж називають суміжним для множини Е.
З означ. випливає, що два різних суміжних інтервали не можуть перетинатися, а можуть лише розташовуватися як на мал. а і мал. б
б

 )
)
Мають один спільний кінець.
Т.9: Множина інтервалів числової прямої, які не перетинаються, скінчена або зчисленна (з числової прямої можна вилучити не більш ніж зчисленну множину інтервалів, які не перетинаються).
Довед.
Нехай на числовій прямій задано множину
інтервалів, які не перетинаються, в
кожному з них можна вибрати по одній
раціональній точці А={δ}.
Множину цих точок позначимо через В.
Маємо А~В.
Оскільки В⊂Q,
то
 ≤а,
тому
≤а,
тому .
.
Т.10: Після вилучення з числової прямої скінченої або зчисленної множини інтервалів, які не перетинаються, одержимо замкнену множину.
Довед. Інтервал – відкрита множина. Об’єднання довільної кількості відкритих множин множина відкрита. Доповнення до відкритої множини є множина замкнена. Зауважимо, що коли множина Е замкнена, обмежена, то існує її найлівіша та найправіша точки, відповідно а і в, тому скінчену або зчисленну множину інтервалів у цьому випадку слід вилучати з відрізка [a;b].
Досконала множина не може мати ізольованих точок. Отже, не може мати місце розташування суміжних інтервалів, як на мал. б. Якщо ж множина обмежена і а – най лівіша, в – най правіша точки, то точки а і в – не можуть бути кінцями суміжних інтервалів, які належать [a;b] (в цих випадках одержуються ізольовані точки).
Т.11: Будь-яку досконалу множину можна одержати вилучивши з числової прямої або відрізка [a;b] скінчену або зчисленну множину інтервалів, які не перетинаються, не мають спільних кінців і не мають своїми кінцями точки а і в.
В теоремі 10 описана будова замкненої множини, а доповнення до замкненої множини є відкрита, тому будь-яка відкрита множина є об’єднанням скінченої або зчисленної множини інтервалів, які не перетинаються.
7. Множина Кантора, підмножини р0 і g0, та їх властивості.
Д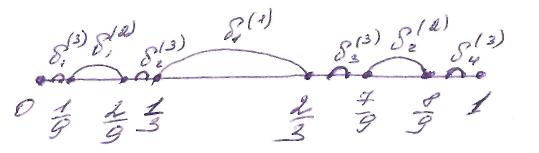 ано
[0;1],
точками
ано
[0;1],
точками
 і
і
 розіб’ємо на три частини і вилучимо
середній інтервал (
;
),
точками
розіб’ємо на три частини і вилучимо
середній інтервал (
;
),
точками
 розіб’ємо кожен з одержаних двох
відрізків на три частини:
розіб’ємо кожен з одержаних двох
відрізків на три частини:
 і вилучимо середні інтервали
і вилучимо середні інтервали
 і т.д., процес можна продовжувати до ∞
і т.д., процес можна продовжувати до ∞
Одержимо дві множини:
G0=δ1(1) δ1(2)δ2(2)
δ1(3)δ2(3)δ3(3)δ4(3)
…
є об’єднанням зчисленної множини
інтервалів, що не мають спільних кінців
і не мають своїми кінцями точок (0;1), G0
– відкрита множина, G0
– відкрита Канторова множина;
δ1(2)δ2(2)
δ1(3)δ2(3)δ3(3)δ4(3)
…
є об’єднанням зчисленної множини
інтервалів, що не мають спільних кінців
і не мають своїми кінцями точок (0;1), G0
– відкрита множина, G0
– відкрита Канторова множина;
P0=[0;1] \ G0 – досконала множина згідно з теоремою 11.
Властивості множин Кантора:
Множині P0 належать, наприклад, кінці всіх вилучених інтервалів і точки 0 та 1. Далі покажемо, множині P0 належать також інші точки, не кінці інтервалів.
Довжина всіх вилучених інтервалів, тобто так звана міра множини G0: mG0=1.
δ1(1):
δ1(2)
δ2(2):
δ1(3)δ2(3)δ3(3)δ4(3):
δi(i),
i=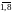 :
:

Міра
mG0=
Міра множини P0:
m P0=m[0;1]- mG0=1-1=0
Множина P0 ніде не щільна на відрізку [0;1].

