14. Збіжність майже скрізь і зюіжність за мірою. Граничний перехід під знаком інтеграла лебега

Збіжність майже скрізь і збіжність за мірою.

Нехай на множині Е визначено послідовність функцій . Позначення: . Послідовність ( збігається до граничної функції f(x) на мн. Е.(Для кожного відповідна числова послідовність збігається до числа f(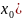 . Називатимемо таку збіжність скрізь на мн.Е.

Озн:Послідовність функцій визначених на мн.Е називатимемо збіжною майже скрізь на мн.Е до функції f(x), якщо рівність має місце майже для всіх хєЕ, тобто міра мн.тих точок з мн.Е для яких рівність не виконується =0.

Приклад:

, x . Очевидно, що для

(1)

f(x) . Але при х=1 відпов. числова послідов -1,1,-1,1... буде розбіжна. Рівність (1) на [0,1] не виконується лише в одній точці х=1. Міра множини , що склад.з 1-єї точки -0. Отже, послідовність збігається до f(x) на [0,1] майже скрізь.

Означ: Послідовність вимірних на мн.Е функцій називається збіжною за мірою на мн.Е до функції f(x), якщо для . . 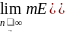Для збіжності за мірою вик. позначення . З озн. випливає, що при міра множини тих точок для яких

(близкість значень) прямує до міри всієї множини Е.

Тв 1: Якщо на Е і на Е, то

Тв 2: Якщо і на мн.Е. Отже, функціон. послідовність може збігається за мірою до різних функцій (екв. між собою).

Тв 3: Якщо збігається до f(x) майже скрізь на мн.Е, то і за мірою на цій множині .

Можна показати, що існують послідовності, які збігаються на Е за мірою, але не збігаються на Е майже скрізь, навіть незбігаються в жодній точці мн.Е.

Висновок: Збіжність за мірою загальніша за збіжність скрізь і майже скрізь .

Граничний перехід під знаком інтеграла Лебега.

Нехай на вимірній мн Е задано послідовність вимірних, обмежених функцій яка в якомусь розумінні (скрізь, майже скрізь, за мірою) збігається до вимірної, обмеженої функції f(x) (вимірність, і обмеженість на Е гарантує інтегрованість за Лебегом на Е зазначених функцій).

Якщо справджується співвідношення (1):

то говорять, що має місце граничний перехід під знаком інтеграла Лебега. У загальному випадку спаввідношення (1) може не мати місця навіть, коли (послідовність збігається скрізь на Е до f(x)).

Т: (Лебега) Нехай на вим.множині Е задано послідовність вимірних, обмежених функцій, яка збігається за мірою до вимірної обмеженої функції f(x). Якщо , то має місце співвідношення

Зауважимо, що сформульована теорема справедлива і у випадку якщо послідовність збігається до f(x), майже скрізь або скрізь на Е. Оскільки, збіжність за мірою загальніша за інші.

Теорема Лебега, не справджується для інтегр.Рімана. Наприклад гранична функція f(x) може бути не інтегрованою за Ріманом: розмістимо всі раціональні числа відрізка [0,1] у вигляді послідовності . Задамо функціон. послідовн. Таким чином

. Оскільки обмежена і міра множини точок розриву=0.

. А гранична функція D(x) не інтегрована за Ріманом. Граничний перехід неможливий.