8. Задача вимірювання множин. Зовнішня і внутрішня міри Лебега та їх властивості.

ОЗН: точна міра множини.

ОЗН: Зауважимо, що з означення точної нижньої межі випливає (характеристичні властивості inf):

1. ∀ S: нижня межа.

2. ∀ ε>0 ∃ S – покриття, якщо ≤m*E+ε

ОЗН: Внутрішньою мірою множини Е⊂[a;b] наз. різниця між довжиною відрізка [a;b] та зовнішньою мірою доповнення С_Е: m_*E=(b-a)-m*C_E

ОЗН: Якщо зовнішня міра множини Е дор. її внутрішній мірі, то така множина наз. вимірною за Лебегом, а спільне значення зовнішньої і внутрішньої мір наз. мірою цієї множини і позначають mE, тобто: mE=m_*E=m*E

О ЗН: Якщо m_*E≠m*E, то множина наз. невимірною за Лебегом.

Ж – Жордано, Л – Лебег.

Всі множини, які вимірні за Жордано є вимірними за Лебегом, причому числові значення цих мір співпадають. Але існують множини, котрі вимірні за Лебегом, але не вимірні за Жордано, тобто клас виміру за Лебегом ширший.

Властивості множин вимірних за Лебегом:

Відзначимо характерні властивості зовнішньої та внутрішньої міри множини.

1. ∀ Е: m^*E≥0, m_*E≥0

2. ∀ E: m_*E≤ m^*E

3. ∀ E₁, E₂ такі, що E₁⊂E₂

m _*E₁≤ m_*E₂

m^*E₁≤m^*E₂

Сформулюймо найважливіші властивості множин m^*E=m_*E, тобто вимірних множин.

Т.1: Якщо множина Е⊂[a;b] вимірна, то вимірною буде і множина С_Е – вимірна.

Дов. Нехай Е – вимірна, тобто m^*E=m_*E= mE. Покажемо, що зовнішня міра m^*С_E=m_*С_E з означення внутрішньої міри випливає m^*С_E=(b-a)-m_*С_E =(b-a)-mE

за означенням внутрішньої міри m^*С_E=(b-a)-m_*С_E(С_Е) =(b-a)-mE. Одержали:

m_*С_E =m^*С_E=(b-a)-mE=mC_E , множина доповнення С_Е – вимірна. Доведено.

При доведенні отримали таку формулу: mC_E=(b-a)-mE.

13. Основні властивості інтеграла лебега. Зв'язок інтеграла рімана з інтегралом лебега

Властивості інтеграла Лебега

Теорема 1. Якщо обмежена і вимірна на множині , причому , то

.

Д оведення. Нехай , ,

Виконаємо -розбиття

Перейдемо до границі (вона існує за попередньою теоремою).

або

.

Перейдемо до границі . В результаті одержимо .Теорему доведено.

Наслідок 1. Якщо , то .

Наслідок 2. Якщо , то .

Наслідок 3. Якщ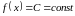о , , то

Теорема 2. Якщо функція обмежена і вимірна на вимірній множині , яка є об’єднанням скінченної або зчисленної кількості вимірних множин , які попарно не перетинаються, то .

Теорема 3. Якщо і обмежені, вимірні і еквівалентні функції на вимірній множині , то .

Доведення.

Позначимо через , .

Враховуючи, що (оскільки ) і маємо:

,

,

Оскільки на множині , то праві частини останніх двох рівностей співпадають. Отже, рівні і ліві частини. Теорему доведено.

Теорема 4. Якщо обмежена і вимірна на вимірній множині , то .

Теорема 5. Якщо і обмежені і вимірні функції на вимірній множині , то .

Теорема 6. Якщо обмежена і вимірна на вимірній множині , то , де .

Теорема 7. Якщо і обмежені і вимірні функції на вимірній множині і майже скрізь на множині виконується нерівність то .

Зв'язок інтеграла Рімана з інтегралом Лебега.

Т: Якщо f(x) інтегрована за Ріманом на [a;b] то вона інтегрована і за Лебегом на цьому відрізку. До того ж (𝑅) =(𝐿)

Лема: Якщо функція f(x) визначена на замкненій обмеженій множині Е, і міра множини іі точок розриву , то функція f(x) вимірна на множині Е.

Доведення: Нехай f(x), (R)- інтегрована на[a;b] (L)−інтегрована функція. Тобто існує (𝐿) . Доведемо, що інтеграли рівні. Розіб’ємо [a;b] на n- частин. Т-розбиття:

Якщо f(x) інтегрована за Лебегом на [a;b], то вона інтегрована на кожному із частинних відрізків . На кожному з відрізків знайдемо , . (f(x)- обмежена на кожному). . На підставі Т.1-ї вл.Лебега: , Просумуємо одержані нерівності в межах

Позначивши , перейдемо до границі при 𝜆(𝑇) в одержаній нерівності. Якщо f(x) (R) –інтегрована на [a;b], то границі лівої і правої частини співпадають і . Отже, рівність інтегралів доведено.

Зауважимо, що обернена теорема немає місця. Існують фун-ії інтегровані за Лебегом, але не інтегровані за Ріманом (наприклад функція Діріхле).