Незчисленність множини дійсних чисел [0;1]. Множини потужності континууму.
Десяткове
представлення дійсних чисел. Відомо,що
кожне дійсне число може бути подано у
вигляді нескінченного десяткового
дробу: рац. – періодичні, іррац. –
неперіодичні. Можна показати, що для
чисел а) |x|≠n+
n,p,k∈N,
p<
.
Існує десяткове представлення у вигляді
нескінченного десяткового дробу; б)
|x|≠n+
Існують два представлення, в яких до
(к-1)
– го знаки співпадають к на одиницю.
Той з дробів, що має менший к-й знак і
має 9 в періоді називається істотним.
Теорема: Будь – яке дійсне число можна подати у вигляді істотного нескінченного десяткового дробу єдиним способом. Будь – який істотно-нескінченний десятковий дріб визначає єдине дійсне число.
Незчисленність множини дійсних чисел [0;1].
Теорема1.
Множина
всіх дійсних чисел інтервалу (0,1)
– незчисленна. Доведення: Припустимо,
що множина
– зчисленна, тоді її елементи можна
подати у вигляді нескінченної послідовності
,
,
,…
…Запишемо
кожне з чисел у вигляді нескінченного
істотного десяткового дробу
=
0,
…
…
=
0,
…
…
=
0,
…
…
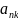Утворено
десятковий дріб 0,
…
…
≠
;
;
;
=
- не 0
в періоді. Цьому дробу відповідає єдине
дійсне число з інтервалу (0,1),
але воно не співпадає з жодним
,
,
,…
,
тому не всі числа множини
розташовані
у вигляді послідовності – супуречність.
Отже,
–
незчисленна.
Теорема2:
Всі
скінченні інтервали, пів інтервали
відрізків – еквівалентні між собою.
Доведення: Досить довести, що довільний
інтервал (а,в)~(0,1),
дійсно лінійна залежність, у=
- взаємооднозначно відображає х=а+у(в-а).
Оскільки приєднання до нескінченної
множини 1-го або кілька елементів не
змінює її потужності
(а,в)~[а,в)~(а,в]~[а,в].
Теорема3: Множина дійсних чисел з інтервалу (0,1) еквівалентна множині всіх дійсних чисел.
Означення: Множина еквівалентна множині всіх дійсних чисел R називається множиною потужності континууму. Позначається с, т.т. R=с.
Теорема4: Множина ірраціональних чисел І=с. Доведення: І=R\Q. Вилучення незчисленної множини R із зчисленної множини Q не змінює її потужності. І~ R, І=с.
Теорема5: Множина дійсних трансцендентних чисел Т має потужність континууму(число, яке не є алгебраїчним наз.трансцедентним)
Теорема6: Множина всіх монотонно – зростаючих послідовн. натуральних чисел має потужність с.
Теорема7: Множина всіх підмножин зчисленної множини має потужність с(узагальнює попередню теорему).
Теорема8: Множина всіх послідовностей натуральних чисел має потужність с.
Теорема9: Якщо елементи множини А= визначаються не більш ніж зчисленною множиною індексів, кожен з яких незалежно від інших пробігає множину потужності континууму с, то ця множина має потужність с.
Теорема10: Об’єднання скінченної або зчисленної системи множин потужності континууму с є множиною потужності с.
Теорема11: Об’єднання континууму множин є множиною потужності континууму.