За критерій перевірки гіпотези беруть статистику
,
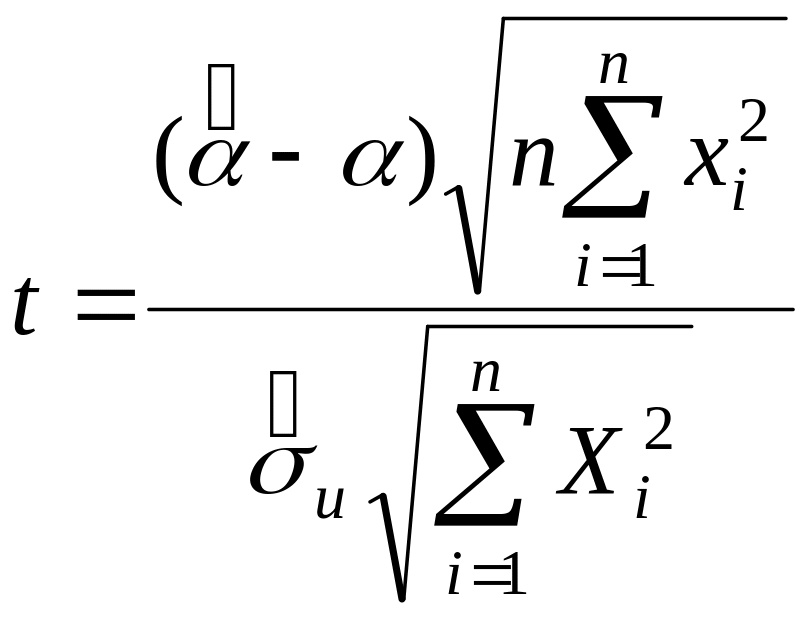(4.20)
яка має розподіл Стьюдента з k=n-2 ступенями свободи.
Для того, щоб при заданому рівні значущості a перевірити нульову гіпотезу при альтернативній гіпотезі , треба обчислити значення критерію, що спостерігається
.
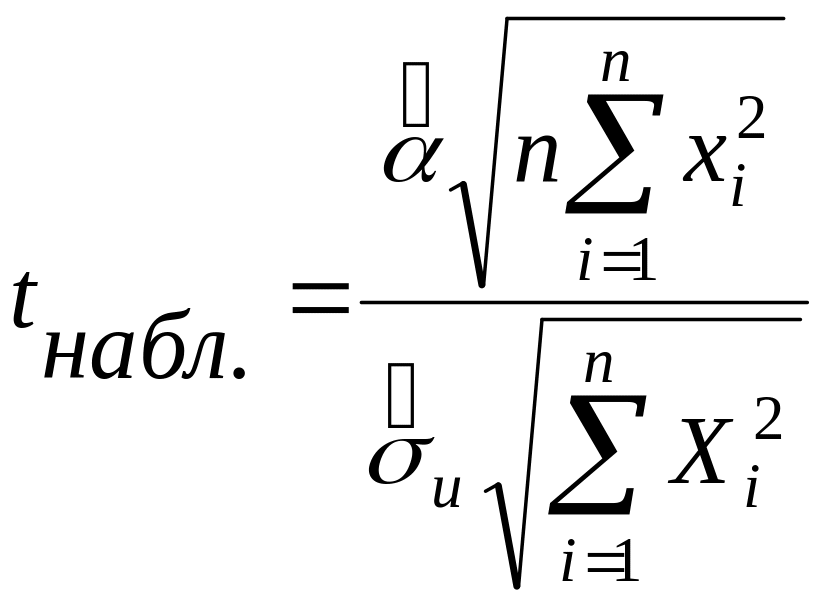(4.21)
Порядок перевірки статистичної гіпотези аналогічний перевірці гіпотези про значущість параметра .
Довірчий
інтервал для параметра
при заданій довірчій ймовірності
,
де
,
визначається відповідно до виразу:
,
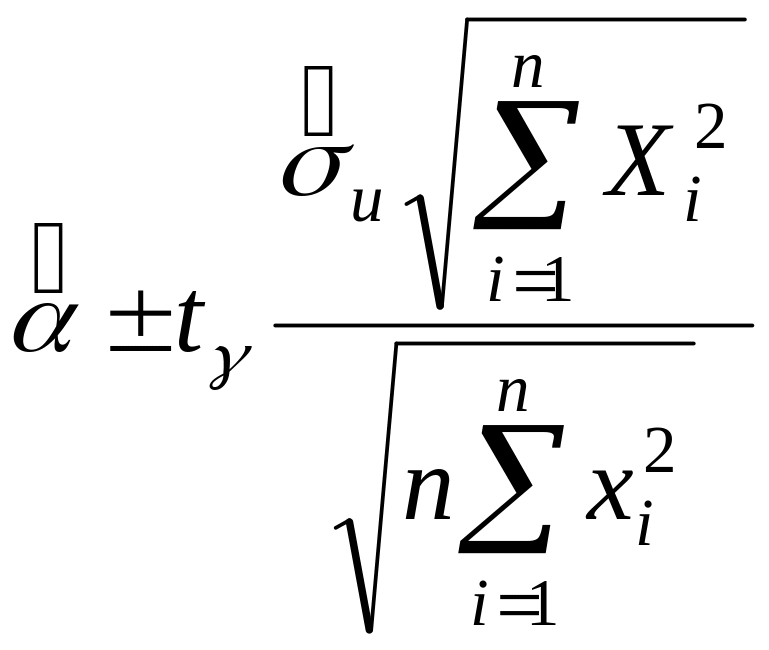(4.22)
де
– критична точка розподілу Стьюдента,
визначається за
табл. В.2 (див.
Додаток В) для числа ступенів свободи
k=n-2
і рівня значущості
,
.
Довірчий інтервал для параметра має вигляд:
.
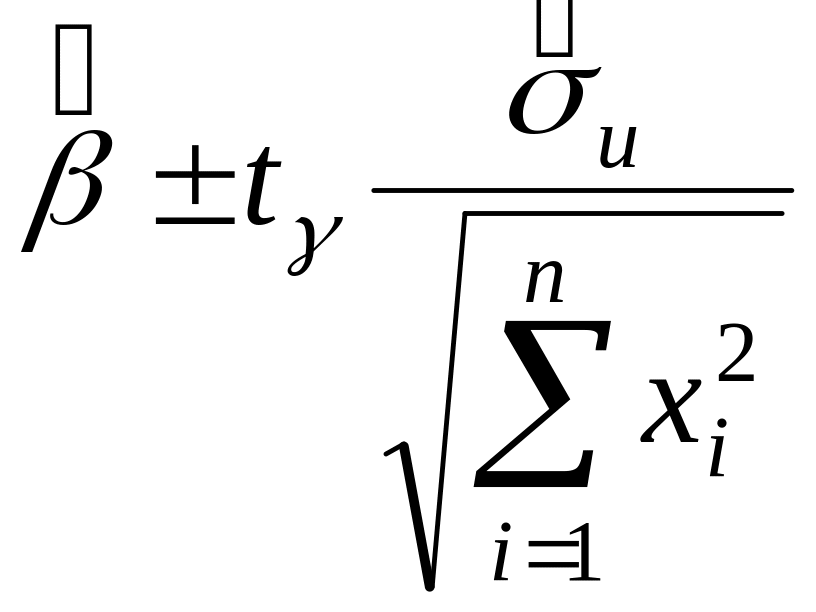(4.23)
4.4 Контрольний приклад
Вибірки випадкових величин X і Y мають такий вигляд: X={352, 373, 411, 441, 462, 490, 529, 577, 641, 692, 743} и Y={166, 153, 177, 201, 216, 208, 227, 238, 268, 268, 274}.
Середні
значення вибірок рівні:
,
.
Точкові оцінки параметрів і мають такі значення:
,
.
Оцінка рівняння лінійної регресії має вигляд:
.
Дисперсії
оцінок параметрів регресії
і
обчислюються відповідно до формул
(4.6),(4.7) і мають такі значення:
,
.
Довірчий інтервал для параметра для рівня значущості =0.05 і числа ступенів свободи k=n-2=9 має вигляд: (38,963; 72,743).
Довірчий інтервал для параметра для рівня значущості =0.05 і числа ступенів свободи k=n-2=9 має вигляд: (-0,95; 1,574 ).
Оцінка
дисперсії випадкової помилки має таке
значення:
Довірчий
інтервал для параметра
для рівня значущості
=0.05
і числа ступенів свободи k=n-2=9
має вигляд: (99,649; 150,166).
Для перевірки статистичної гіпотези про значущість параметра висувається гіпотеза при альтернативній гіпотезі .
Значення
критерію, що спостерігається
3,85423,
критичне значення критерію
для двосторонньої критичної області
дорівнює
=2,26.
Оскільки
>
,
то гіпотеза
відхиляється.
Для
перевірки статистичної гіпотези про
значущість параметра
висувається гіпотеза
при альтернативній гіпотезі
.
Значення критерію, що спостерігається 11,49179, критичне значення критерію для двосторонньої критичної області дорівнює =2,26. Оскільки > , то гіпотеза відхиляється.
4.5 Порядок виконання роботи
По вибірках реалізацій випадкових величин X і Y обсягом n=30 зробити регресійний аналіз.
Вибірка випадкової величини X має загальний вигляд для усіх варіантів і містить значення:
X={9,8; 15,4; 8,6; 7,6; 10,2; 12,6; 6,6; 10,3; 6,3; 14,8; 11,1; 10,6; 7,3; 12,2; 8,4; 12,7; 7,9; 13,0; 11,5; 13,0; 9,4; 7,2; 11,3; 10,7; 18,5; 13,0; 5,9; 9,3; 10,1; 7,1}.
Вибірки випадкової величини Y для кожного варіанта лабораторної роботи наведені в табл.A.2 (див. Додаток А.).
Вивчити основні етапи регресійного аналізу.
По вибірках реалізацій випадкових величин X і Y обсягів n=30 побудувати діаграму розсіювання і зробити попередній висновок про характер зв'язку аналізованих випадкових величин X і Y.
Виписати розрахункові формули для обчислення точкових оцінок параметрів регресії, дисперсій оцінок параметрів регресії, оцінок дисперсії випадкової помилки.
За допомогою ЕОМ обчислити точкові оцінки параметрів регресії, дисперсій оцінок параметрів регресії, оцінку дисперсії випадкової помилки
Записати рівняння регресії.
На діаграму розсіювання нанести лінію, що відповідає оцінці лінійної регресії.
Перевірити гіпотези про значущість параметрів регресії і при рівні значущості a =0.05.
Побудувати довірчі інтервали для параметрів і при заданій довірчій ймовірності =0.95.
Зробити висновки на основі аналізу результатів проведеного регресійного аналізу.
Оформити звiт про лабораторну роботу.
4.6 Зміст звіту
Звіт має містити: мету роботи, основні розрахункові формули, результати обчислень за цими формулами, точкові оцінки та довірчі інтервали для оцінок параметрів регресії, рівняння регресії, необхідні висновки про перевірку гіпотез про значущість параметрів регрессії
4.7 Контрольні запитання та завдання
1. Які основні етапи містить у собі регресійний аналіз?
2. Записати лінійне рівняння парної регресії.
3. За яким методом здійснюється оцінювання параметрів регресії?
4. Записати формули для точкових оцінок параметрів регресії.
5. Записати розрахункові формули для обчислення дисперсій оцінок параметрів регресії, оцінки дисперсії випадкової помилки.
6. Який порядок перевірки статистичних гіпотез про значущість параметрів регресії?
7. Як будуються довірчі інтервали для параметрів і ?