2 Параметричне оцінювання закону розподілу випадкової величини
2.1 Мета роботи
Вивчити методи параметричного оцінювання законів розподілу випадкової величини, навчитися застосувати ці методи під час аналізу статистичних даних .
2.2 Методичні вказівки з організації самостійної роботи студентів
Попередньою вимогою для виконання роботи є засвоєння таких теоретичних знань: закони розподілу неперервних випадкових величин (показниковий, рівномірний, нормальний), функція та щільність розподілу, параметри законів розподілу випадкових величин, незміщені та ефективні оцінки, математичне сподівання, дисперсія, середнє квадратичне відхилення, точкові та інтервальні оцінки математичного сподівання та дисперсії.
2.3 Основні положення
Параметричний засіб оцінювання розподілу полягає в тому, що за результатами вибірки оцінюються невідомі параметри розподілу, тип якого відомий або передбачається.
Оцінювання параметрів містить у собі два етапи: точкове оцінювання й інтервальне оцінювання.
Точковою
оцінкою невідомого параметра
називають функцію від вибіркових значень
випадкової величини, реалізація якої
приймається за невідоме значення
параметра
.
Для того, щоб оцінку
можна було використовувати замість
невідомого параметра
,
вона має бути спроможною, незсуненою
та ефективною.
Спроможною і незсуненою оцінкою математичного сподівання випадкової величини X є середнє арифметичне:
.
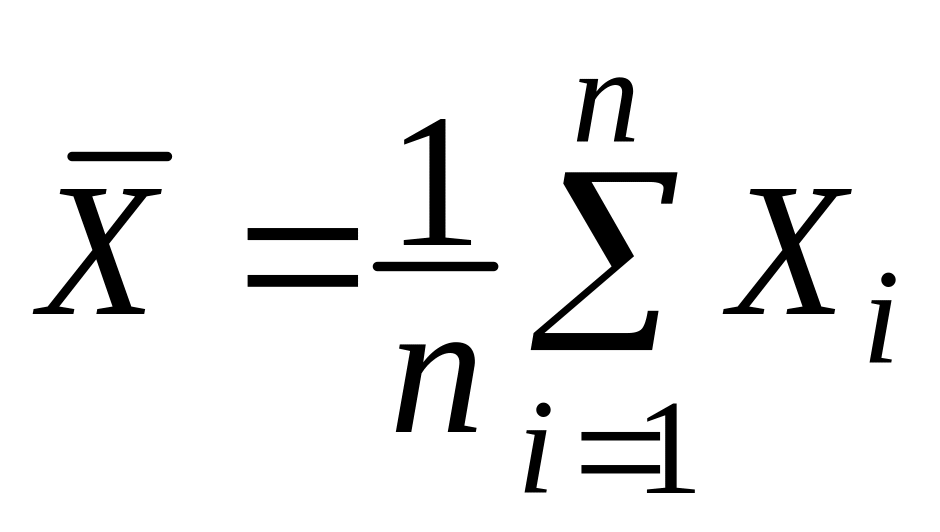(2.1)
За спроможну і незсунену оцінку дисперсії випадкової величини X беруть виправлену вибіркову дисперсію:
.
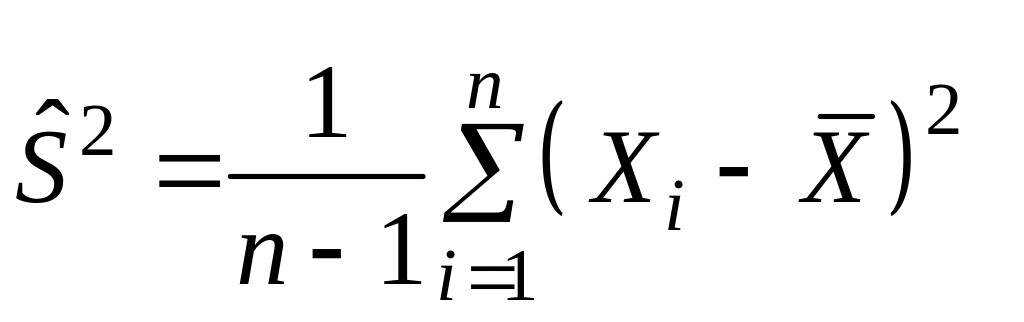(2.2)
Точковими
оцінюваннями параметрів a
і
нормального
розподілу є
;
(2.3)
.
(2.4)
Для
показникового розподілу точкове
оцінювання параметра
визначається в такий спосіб:
.
(2.5)
За точкові оцінювання параметрів а і b рівномірного розподілу беруть такі величини:
.
(2.6)
Під інтервальним оцінюванням розуміють інтервал, який називають довірчим, межі якого залежать від вибіркових значень випадкової величини X і який із заданою ймовірністю містить істинне значення оцінюваного параметра.
Довірчий
інтервал для математичного сподівання
випадкової величини при заданій довірчій
ймовірності
визначається відповідно до виразу:
,
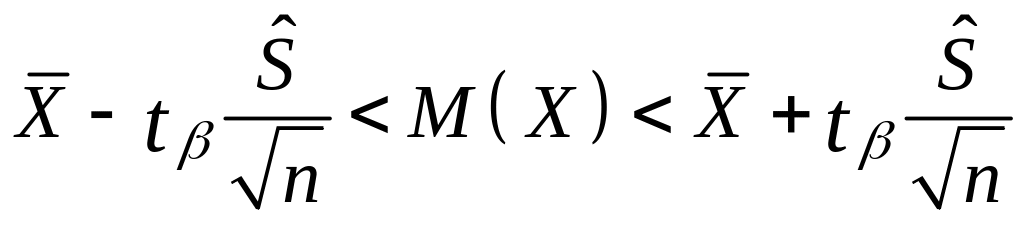(2.7)
де
– математичне сподівання випадкової
величини X;
– критична
точка розподілу Стьюдента, визначається
за табл.В.2 для числа ступенів свободи
k=n-1
і рівня значущості
.
Довірчий інтервал для дисперсії має вигляд:
,
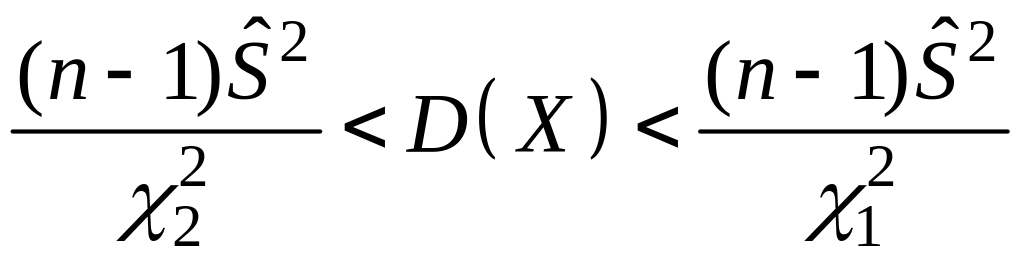(2.8)
де
– дисперсія випадкової величини X;
– критичні
точки розподілу
Пірсона, значення яких визначається за
таблицею В.3 за числом ступенів свободи
k=n–1,
а також за рівнем значущості a/2
для
і (1-a
/2)
для
.
2.4 Контрольні приклади
Приклад 2.1. Даний приклад є продовженням прикладу 1.1.
Для вибірки реалізації випадкової величини (таблиця 1.2) обчислити точкові оцінювання математичного сподівання і дисперсії. Зробити обчислення оцінювання параметрів нормального закону розподілу, відносно якого була висунута гіпотеза в завданні 1 (приклад 1.1).
Використовуючи отримані оцінки параметрів розподілу, побудувати графіки теоретичних щільності розподілу і функції розподілу нормального закону розподілу.
Для заданої довірчої ймовірності b=0.95 оцінити довірчі інтервали для математичного сподівання і дисперсії.
Розрахунок
Знайдемо середнє арифметичне
=
=
та виправлену вибіркову дисперсію і середнє квадратичне відхилення
=
=
=9,204;
=
.
Точковими оцінюваннями параметрів а і нормального розподілу є
=5,94 ; =3,034.
Використовуючи отримані оцінки параметрів розподілу, щільність розподілу і функція розподілу мають такий вигляд:
=
;
=
.
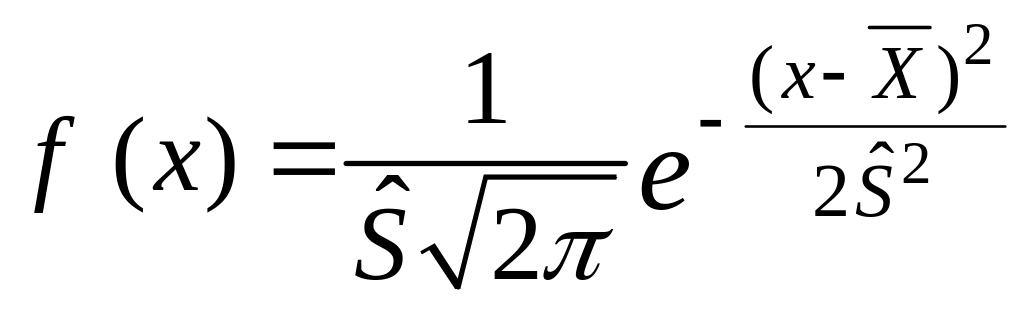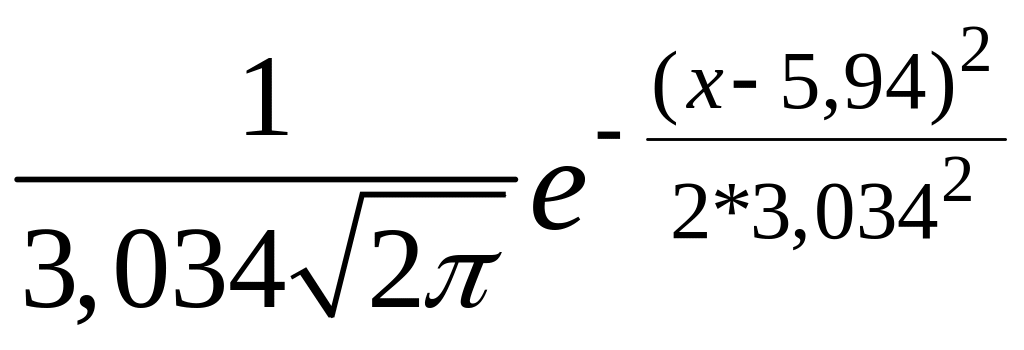Побудуємо графіки теоретичних щільності розподілу і функції розподілу , вираховуючи їх значення для межі кожного інтервалу. Дані наведено в таблицях 2.1, 2.2.
Таблиця 2.1 – Щільність розподілу
|
-0,97 |
0,765 |
2,5 |
4,235 |
5,97 |
7,705 |
9,44 |
11,175 |
12,91 |
|
0,010 |
0,031 |
0,069 |
0,113 |
0,132 |
0,112 |
0,088 |
0,030 |
0,009 |
Таблиця 2.2 – Функція розподілу
|
-0,97 |
0,765 |
2,5 |
4,235 |
5,97 |
7,705 |
9,44 |
11,175 |
12,91 |
|
0,01 |
0,04 |
0,13 |
0,29 |
0,50 |
0,72 |
0,87 |
0,96 |
0,99 |
На рис 2.1 і рис 2.2 зображено графіки теоретичної щільності та функції розподілу нормального закону розподілу.
Р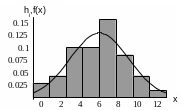
исунок
2.1– Гістограма відносних частот та
щільність розподілу
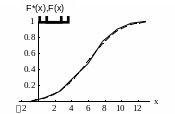
Рисунок 2.2 – Емпірична та теоретична (пунктир) функції розподілу
Побудуємо
довірчі інтервали для математичного
сподівання та дисперсії випадкової
величини, що досліджується. Для цього
задамо довірчу ймовірність
.
Тоді рівень значущості
.
Оскільки вибірка має
40 елементів
(
),
то число ступенів свободи складатиме
.
Знайдемо значення критичної точки
розподілу Стьюдента:
.
Тоді довірчий інтервал для математичного
сподівання згідно з формулою (2.7) матиме
вигляд:
або
.
Довірчий
інтервал для дисперсії обчислимо за
формулою (2.8). Для цього знайдемо критичні
точки розподілу
за числом ступенів свободи k=n–1=39,
а також за рівнем значущості a/2=0,25
для
і (1-a
/2)=0,975
для
:
і
(Дод.В).
Тоді довірчий інтервал для дисперсії
матиме вигляд:
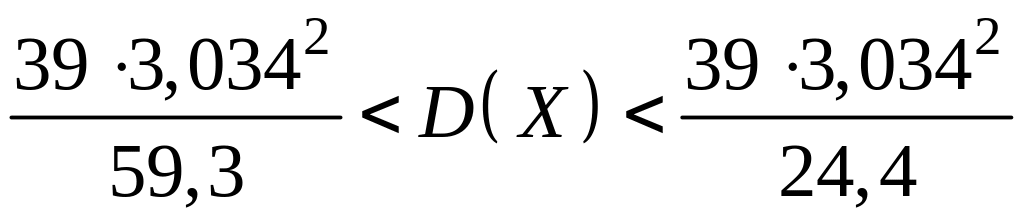або
.
Приклад 2.2. Даний приклад є продовженням прикладу 1.2.
Для вибірки реалізації випадкової величини (таблиця 1.5) обчислити точкові оцінки математичного сподівання і дисперсії. Зробити обчислення оцінки параметра показникового закону розподілу, відносно якого була висунута гіпотеза в завданні 1 (приклад 1.2).
Використовуючи отриману оцінку параметра розподілу, побудувати графіки теоретичних щільності розподілу і функції розподілу показникового закону розподілу.
Для заданої довірчої ймовірності b=0.95 оцінити довірчі інтервали для математичного сподівання і дисперсії.
Розрахунок
Знайдемо середнє арифметичне
=
=
та виправлену вибіркову дисперсію і середнє квадратичне відхилення
=
=
=1,219;
=
.
Для
показникового розподілу точкове
оцінювання параметра
визначається в такий спосіб:
.
Використовуючи отримане оцінювання параметра розподілу, щільність розподілу і функція розподілу мають такий вигляд:
=
;
=
=
.
Побудуємо графіки теоретичних щільності розподілу і функції розподілу , вираховуючи їх значення для межі кожного інтервалу. Дані наведено в таблицях 2.3, 2.4.
Таблиця 2.3 – Щільність розподілу
|
0,02 |
0,721 |
1,422 |
2,123 |
2,824 |
3,525 |
4,226 |
4,927 |
5,628 |
6,329 |
7,03 |
|
0,963 |
0,484 |
0,243 |
0,122 |
0,061 |
0,030 |
0,016 |
0,008 |
0,004 |
0,002 |
0,001 |
Таблиця 2.4 – Функція розподілу
|
0,02 |
0,721 |
1,422 |
2,123 |
2,824 |
3,525 |
4,226 |
4,927 |
5,628 |
6,329 |
7,03 |
|
0,019 |
0,507 |
0,753 |
0,876 |
0,938 |
0,969 |
0,984 |
0,992 |
0,996 |
0,998 |
0,999 |
На рис 2.3 і рис 2.4 зображено графіки теоретичної щільності та функції показникового закону розподілу.
Рисунок 2.3 – Гістограма відносних частот та щільність розподілу
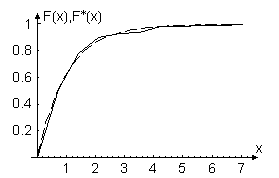
Рисунок 2.4 – Емпірична та теоретична (пунктир) функції розподілу
Побудуємо
довірчі інтервали для математичного
сподівання та дисперсії випадкової
величини, що досліджується. Для цього
задамо довірчу ймовірність
.
Тоді рівень значущості
.
Оскільки вибірка має
100 елементів
(
),
то число ступенів свободи складатиме
.
Знайдемо значення критичної точки
розподілу Стьюдента:
.
Тоді довірчий інтервал для математичного
сподівання згідно з формулою (2.7) матиме
вигляд:
або
.
Довірчий інтервал для дисперсії обчислимо за формулою (2.8). Для цього знайдемо критичні точки розподілу за числом ступенів свободи k=n–1=99, а також за рівнем значущості a/2=0,025 для і (1-a /2)=0,975 для : =74,2 і =129,6. Тоді довірчий інтервал для дисперсії матиме вигляд:
або
.
Приклад 2.3. Даний приклад є продовженням прикладу 1.3.
Для вибірки реалізації випадкової величини (табл. 1.8) обчислити точкові оцінки математичного сподівання і дисперсії. Зробити обчислення оцінки параметра рівномірного закону розподілу, відносно якого була висунута гіпотеза в завданні 1 (приклад 1.3).
Використовуючи отриману оцінку параметра розподілу, побудувати графіки теоретичних щільності розподілу і функції розподілу рівномірного закону розподілу.
Для заданої довірчої ймовірності b=0.95 оцінити довірчі інтервали для математичного сподівання і дисперсії.
Розрахунок
Знайдемо середнє арифметичне
=
=
та виправлену вибіркову дисперсію і середнє квадратичне відхилення
=
=
=6,7;
=
.
Для
рівномірного розподілу точкові оцінки
параметрів
і
визначаються в такий спосіб:
.
Використовуючи отримані оцінки параметрів розподілу, щільність розподілу і функція розподілу мають такий вигляд:
=
;
=
.
Побудуємо графіки теоретичних щільності розподілу і функції розподілу , вираховуючи їх значення для межі кожного інтервалу. Дані наведено в таблицях 2.3, 2.4.
Таблиця 2.5 – Щільність розподілу
|
0,18 |
1,051 |
1,922 |
2,793 |
3,664 |
4,535 |
5,406 |
6,277 |
7,148 |
8,019 |
8,89 |
|
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
0,115 |
Таблиця 2.6 – Функція розподілу
|
0,18 |
1,051 |
1,922 |
2,793 |
3,664 |
4,535 |
5,406 |
6,277 |
7,148 |
8,019 |
8,89 |
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
На рис 2.5 і рис 2.6 зображено графіки теоретичної щільності та функції рівномірного закону розподілу.
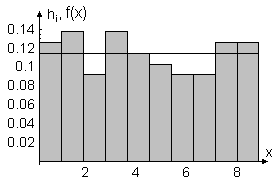
Рисунок 2.5 – Гістограма відносних частот та щільність розподілу
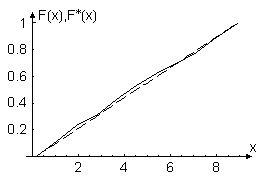
Рисунок 2.6 – Емпірична та теоретична (пунктир) функції розподілу
Побудуємо довірчі інтервали для математичного сподівання та дисперсії випадкової величини, що досліджується. Для цього задамо довірчу ймовірність . Тоді рівень значущості . Оскільки вибірка має 100 елементів ( ), то число ступенів свободи складатиме . Знайдемо значення критичної точки розподілу Стьюдента: . Тоді довірчий інтервал для математичного сподівання згідно з формулою (2.7) матиме вигляд:
або
.
Довірчий інтервал для дисперсії обчислимо за формулою (2.8). Для цього знайдемо критичні точки розподілу за числом ступенів свободи k=n-1=99, а також за рівнем значущості a/2=0,025 для і (1-a /2)=0,975 для : =74,2 і =129,6. Тоді довірчий інтервал для дисперсії матиме вигляд:
або
.
2.5 Порядок виконання роботи
Продовжити виконання роботи 1.
За допомогою ЕОМ зробити обчислення оцінок параметрів розподілу, тип якого передбачається (за результатами лабораторної роботи 1 даних методичних вказівок).
Використовуючи отримані оцінки параметрів розподілу, побудувати за допомогою ЕОМ графіки теоретичних щільності розподілу і функції розподілу, що відповідають висунутій в роботі 1 гіпотезі.
Побудову графіків необхідно виконати на гістограмі й емпіричній функції розподілу, вираховуючи і для межі кожного інтервалу.
Для заданої вибірки обчислити точкові оцінки математичного сподівання і дисперсії та для заданої довірчої ймовірності b=0.95 оцінити довірчі інтервали для математичного сподівання і дисперсії.
Дані для виконання роботи подано в табл.А.1.
2.6 Зміст звіту
Звіт має містити: мету роботи, основні розрахункові формули, графіки теоретичних щільності розподілу і функції розподілу, що відповідають висунутій в роботі 1 гіпотезі, точкові оцінки та довірчі інтервали для математичного сподівання і дисперсії, висновки.
2.7 Контрольні запитання та завдання
1. Що таке точкові оцінки ?
2. Які властивості повинні мати точкові оцінки ?
3. Що є точковою оцінкою математичного сподівання ?
4. Що є точковою оцінкою дисперсії і які властивості вона має ?
5. Що таке інтервальні оцінки ?
6. Як обчислюються інтервальні оцінки для математичного сподівання і дисперсії ?
7. Наведіть формули для оцінок параметрів нормального, показникового і рівномірного розподілів.