Задание 5.4

Найти наибольшее и наименьшее значения функции

в области, ограниченной прямыми: ; ; .

Решение:

Построим область с заданными ограничениями (рис. 6).

Рис. 6

Точки, в которых функция принимает наибольшее и наименьшее значения, могут находиться как внутри области, так и на ее границе.

Рассмотрим внутреннюю область. Найдем частные производные

В точке экстремума они должны обращаться в нуль. Найдем стационарные точки, решая систему:

Получаем точку М₁( , ), значение функции в которой

Следовательно, имеется только одна точка, в которой может достигаться наименьшее или наибольшее значение функции во внутренней области.

Теперь исследуем функцию на границах области:

1. На отрезке ОВ:

находим производную:

и решаем уравнение:

Получаем одну стационарную точку на отрезке ОВ М₂(0; ), находим значение функции в точке М₂ и на концах отрезка ОВ

2. Аналогично исследуем отрезок ОА:

получаем стационарную точку М₃ , находим значения функции z на концах отрезка ОА и в точке М₃

3. Исследуем отрезок АВ:

Получаем стационарную точку М₄( , )

Сравнивая все полученные значения функции z в стационарных точках и на границе области, заключаем, что

z_наиб.=z(A)=z(B)=3; z_наим.=z(M₁)= .

КРАТНЫЕ ИНТЕГРАЛЫ

Тема 6. Двойные и тройные интегралы.

Задание 6.1

Изменить порядок интегрирования в повторном интеграле

Решение:

Построим область интегрирования по данному интегралу (рис. 7).

Рис. 7

Область интегрирования G ограничена линиями , , , .

Прямая разбивает ее на две области:

G1: , и G2: ,

Имеем

= .

Задание 6.2

Сделать чертеж и найти объем тела, ограниченного поверхностями , , , .

Решение:

Рис.8

Данное тело сверху ограничено параболическим цилиндром (рис. 8). По формуле находим:

.

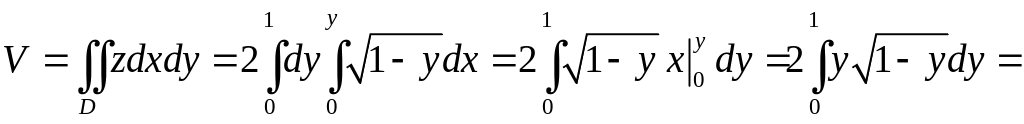
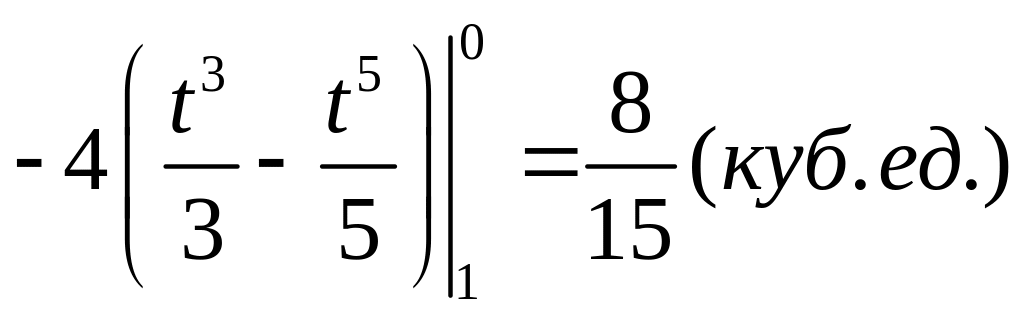Задание 6.3

Вычислить площадь плоской области D, ограниченной

заданными линиями.

Решение:

Данная плоская фигура ограничена снизу параболой

, сверху прямой (рис. 9).

Следовательно,

.

Рис. 9

Задание 6.4

Вычислить , где V ограничено поверхностями:

Решение:

По заданным поверхностям строим область D интегрирования (рис. 10).

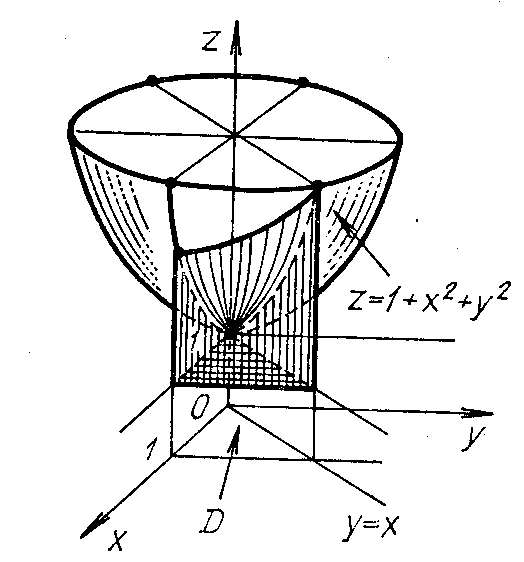
В области V справедливы неравенства: , , .

Тогда

.

Рис. 10

Задание 6.5

С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями: .

Решение:

Уравнение определяет параболоид вращения, остальные поверхности: -плоскости.

Искомое геометрическое тело изображено на рис.11

Объем данного тела равен:

Рис. 11

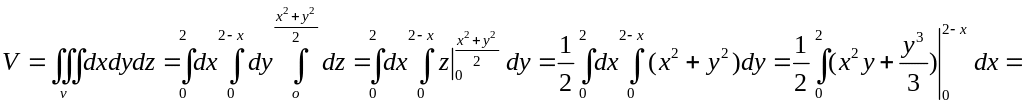
КРиволинейные и поверхностные ИНТЕГРАЛЫ

Тема 7. Криволинейные и поверхностные интегралы.

Задание 7.1

Вычислить криволинейный интеграл , если линия - дуга параболы , расположенная между точками и :

Решение:

Применим формулу

.

В данном случае , , ,

получим

.

Задание 7.2

Вычислить поверхностный интеграл второго рода ,

где S –внешняя сторона части круга , расположенная в первом октанте.

Решение:

Имеем .

Обозначим через и -проекции поверхности S на координатные плоскости и соответственно, а данный интеграл I рассмотрим как сумму трех интегралов:

, ,

Для первого из которых , для второго и для третьего .

Применив к каждому из них формулу для вычисления поверхностного интеграла второго рода, получим

, , .

Области и являются четвертями кругов единичного радиуса, расположенными в соответствующих координатных плоскостях, поэтому интеграл (площадь четверти круга). Перейдем к полярным координатам для вычисления интегралов и , положив для ,

для . В обоих случаях .

Тогда

.

.

Следовательно, .

V. Задания к контрольным работам