Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.

Задание 3.1

Вычислить интегралы

Решение:

Данный интеграл можно вычислить путем внесения под знак дифференциала:

Задание 3.2

Вычислить интеграл

Решение:

Воспользуемся формулой интегрирования по частям :

Полагая , отсюда найдем ,

.

Задание 3.3

Вычислить интеграл

Решение:

Разложим подынтегральную функцию на простейшие дроби, используя метод неопределенных коэффициентов:

=

Приведя правую часть равенства к общему знаменателю и умножая обе части равенства на (х-2)²(х²+2), получаем:

Приравнивая коэффициенты при х⁰, х¹, х², х³ получим систему уравнений:

Решая эту систему, имеем: .

Следовательно: =

Таким образом = =

= =

= .

Задание 3.4

Вычислить интеграл

Решение:

Применим универсальную тригонометрическую подстановку , тогда , , .

.

=

Выполним обратную замену переменной, получим:

Задание 3.5

Вычислить определенные интегралы:

а)

Решение:

Учитывая, что ,

сделаем замену , тогда .

Найдем новые пределы интегрирования:

Используя формулу Ньютона-Лейбница

п олучим:

.

б) .

Решение:

Полагая ; . Тогда ; ;

По формуле интегрирования по частям в определенном интеграле получаем:

.

Задание 3.6

Вычислить несобственные интегралы или установить их расходимость: а)

Решение:

Следовательно – расходится.

б)

Решение:

В соответствии с определением несобственного интеграла от неограниченной функции в окрестности точки имеем:

, таким образом исходный интеграл сходится.

Задание 3.7

Вычислить площадь фигуры, ограниченной линиями: , .

Решение:

Построим графики данных функций (рис. 4).

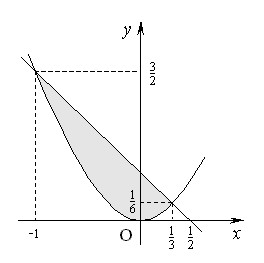
Рис. 4

Найдем точки пересечения данных кривых:

, .

Находим площадь криволинейной трапеции по формуле:

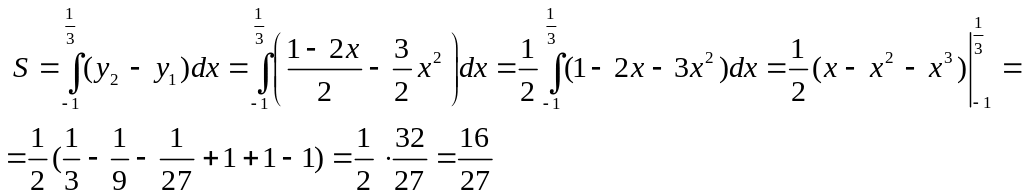
Следовательно,

Задание 3.8

Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями: и .

Решение:

Н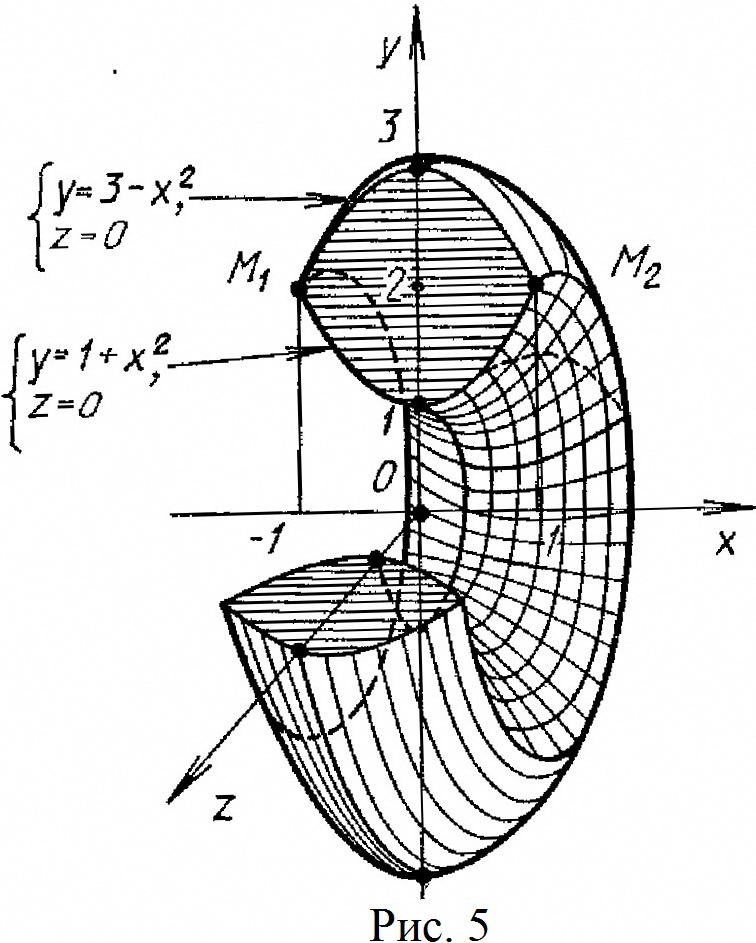 аходим точки пересечения данных парабол, решая систему уравнений:

,

Объем тела образованного вращением данной фигуры вокруг оси OX получаем как разность объемов . Вычислим по формуле:

Получим

и .

Таким образом,

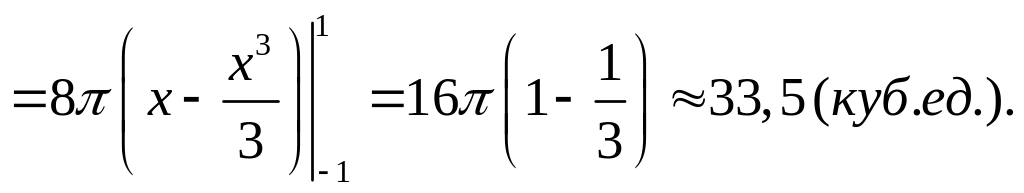
На рис.5 изображены плоская фигура в плоскости OXY и тело (из него вырезана четвертая часть), полученное вращением данной фигуры вокруг оси OX.

РЯДЫ.

Тема 4. Числовые и степенные ряды. Задание 4.1

Исследовать на сходимость ряды с положительными членами:

а)

Решение:

Применим второй признак сравнения.

Сравним данный ряд с рядом , который расходится как обобщенный гармонический ряд , т.к. при

, ,

.

Значит, исходный ряд расходится.

б)

Решение:

Применим признак Даламбера.

.

Так как q= 1, то исходный ряд расходится.

в)

Решение:

Применим радикальный признак Коши.

, т. е. исходный ряд сходится.