Задание 4.2

Исследовать на условную и абсолютную сходимость знакочередующийся ряд: .

Решение:

Ряд

является знакочередующимся рядом.

Для исследования его на сходимость применим признак Лейбница. Так как

1) - члены ряда по абсолютной величине убывают

и 2) => оба условия признака Лейбница выполняются, то исходный ряд сходится.

Исследуем ряд, составленный из абсолютных величин данного ряда . Сравним его с рядом .

– это обобщенный гармонический ряд, он сходится, так как , тогда знакочередующийся ряд является абсолютно сходящимся рядом.

Задание 4.3

Найти область сходимости степенного ряда:

Решение:

Найдем радиус сходимости R степенного ряда

Так как , , то

.

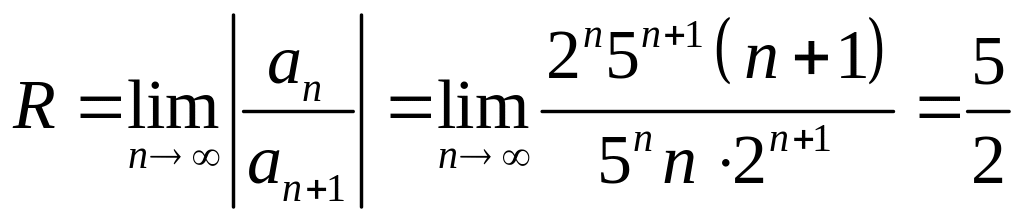Это означает, что ряд сходится абсолютно внутри интервала и расходится вне этого интервала. Точки и требуют дополнительного исследования.

1) При ряд принимает вид . Это гармонический ряд. Известно, что этот ряд расходится.

2) При ряд принимает вид . Это ряд Лейбница, который сходится условно.

Следовательно, область сходимости исходного степенного ряда .

Задание 4.4

Разложить функцию в ряд Тейлора в окрестности точки :

Решение:

Так как ,

разложим в ряд Тейлора в окрестности точки , используя формулу:

(*)

В ряд Маклорена для cosx (формула (*)) вместо подставим , затем домножим полученное выражение на (-1) и прибавим 2,

тогда получим:

.

Задание 4.5

а) С помощью разложения в ряд вычислить приближенно с точностью 0,0001 значения:

Решение:

Воспользуемся разложением в степенной ряд функции по формуле Маклорена

.

Так как то

Получили знакочередующийся числовой ряд. Для того чтобы вычислить значения функции с точностью необходимо, чтобы первый отбрасываемый член был меньше (из следствия признака Лейбница).

Имеем

С заданной степенью точности:

.

б) Используя разложение подынтегральной функции в степенной ряд, вычислить определенный интеграл с точностью до 0,001.

Решение:

Воспользуемся биномиальным рядом , (*)

Преобразуем подынтегральную функцию:

Получили бином вида где а Подставляя в (*), имеем

. Поскольку уже третий член полученного ряда меньше , т.е , то с точностью до 0,001 получим

Задание 4.6

Разложить в ряд Фурье функцию с периодом , заданную на промежутке :

Решение:

Так как данная функция кусочно-монотонная и ограниченная, то она разлагается в ряд Фурье.

Находим коэффициенты ряда Фурье:

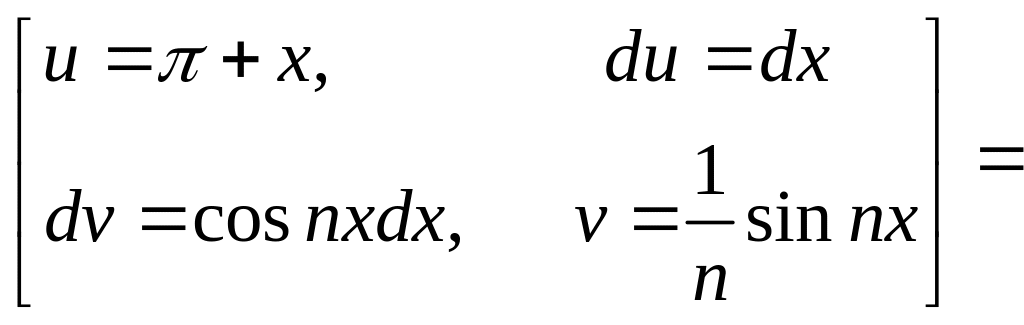
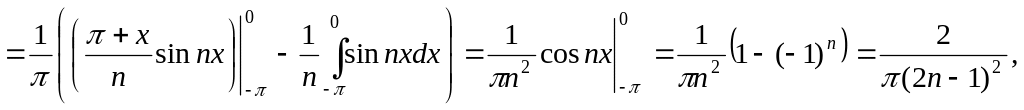
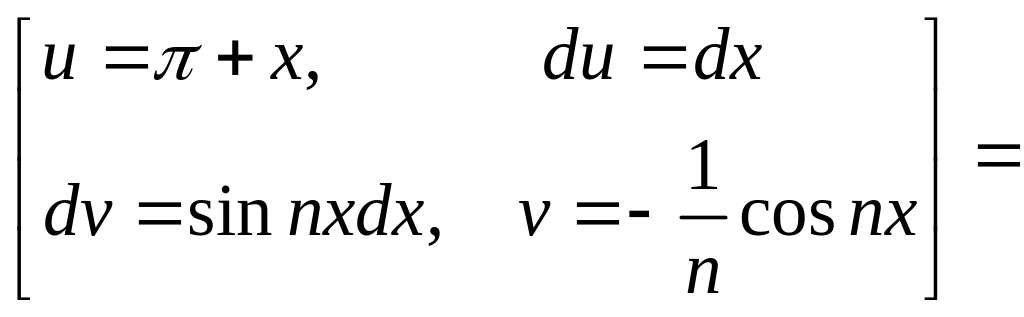
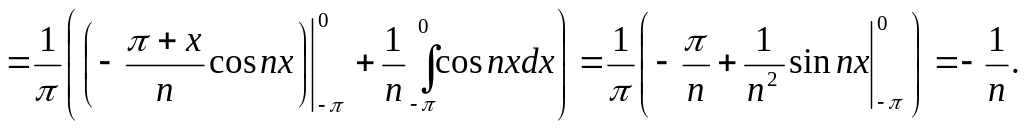
Тогда ряд Фурье для данной функции примет вид

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Тема 5. Функции нескольких переменных.

Задание 5.1

Найти полный дифференциал функции .

Решение: Вычислим частные производные функции :

Полный дифференциал находим по формуле

Тогда .

Задание 5.2

Дана функция . Показать, что она удовлетворяет уравнению .

Решение: Найдем частные производные 1-го и 2-го порядков от функции :

,

, ,

Подставим их в заданное уравнение:

Следовательно, функция удовлетворяет указанному уравнению.

Задание 5.3

Даны функция , точка и вектор .

Найти:

1) в точке ,

2) производную в точке по направлению вектора .

Решение:

1) Найдем градиент функции в точке по формуле

Вычислим частные производные функции и их значения в точке .

, .

Тогда .

2)Найдем направляющие косинусы вектора :

.

(из п.1)

Подставив в формулу производной по направлению

найденные значения, получим

.