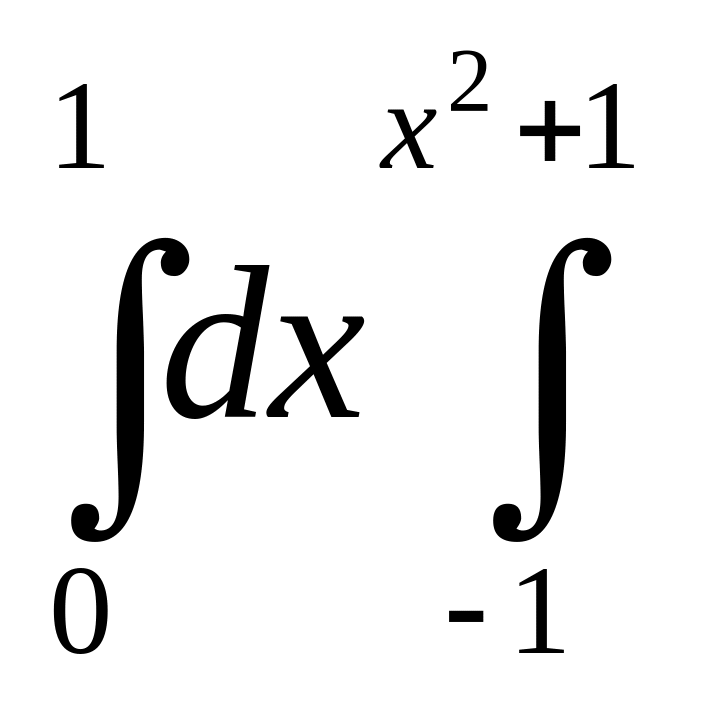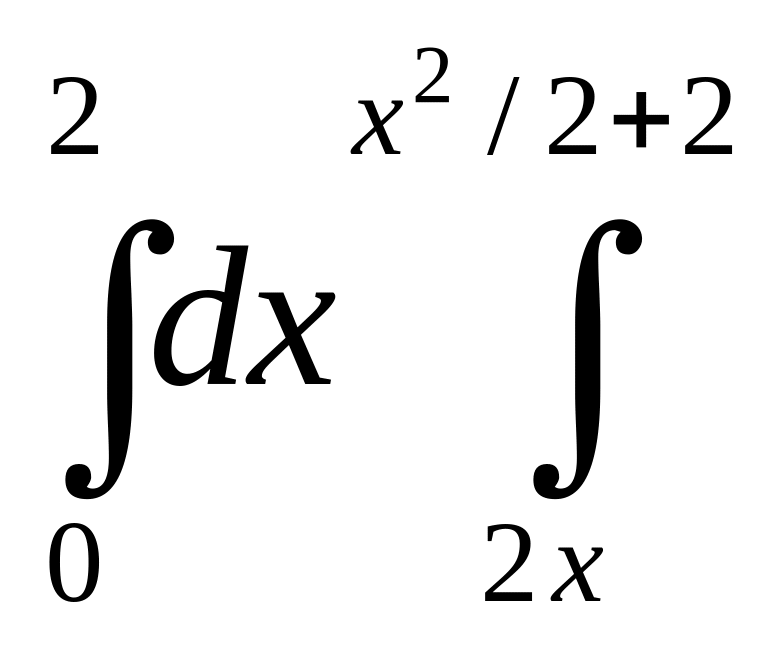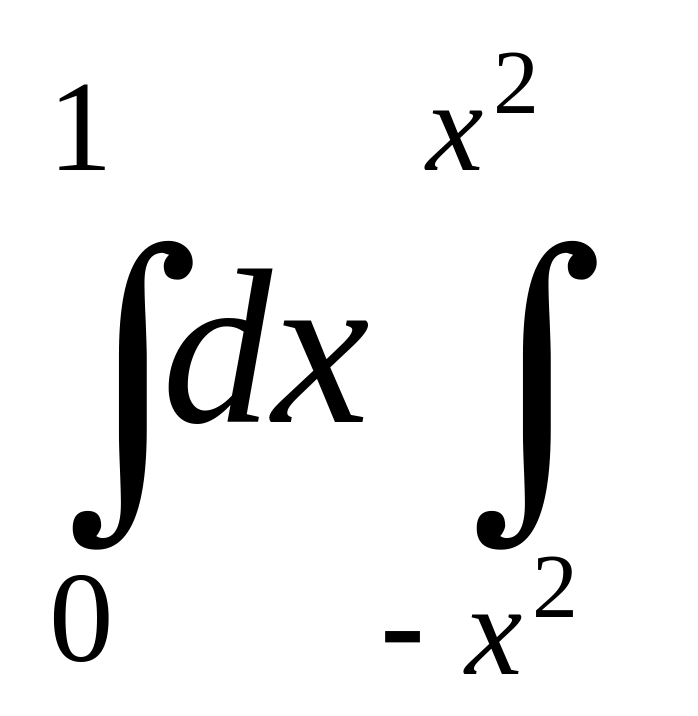- •Содержание
- •ВВеДение
- •I.Требования к оформлению контрольных работ
- •II.Формирование заданий для контрольных работ
- •Іiі. Теоретическое содержание курса «Математический анализ» введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Тема 2. Дифференцирование функции одной переменной. Исследование функций с помощью производных.
- •Неопределенный интеграл. Определенный интеграл и его приложения.
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Тема 4. Числовые и степенные ряды.
- •Функции нескольких переменных
- •Тема 5. Функции нескольких переменных.
- •Кратные интегралы
- •Тема 6. Двойные и тройные интегралы.
- •КРиволинейные и поверхностные интегралы
- •Тема 7. Криволинейные и поверхностные интегралы.
- •Іv. Решение типовых заданий введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Задание 1.6
- •Тема 2. Дифференцирование функций одной переменной. Исследование функций с помощью производных.
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Тема 4. Числовые и степенные ряды. Задание 4.1
- •Задание 4.2
- •Задание 4.3
- •Задание 4.4
- •Задание 4.5
- •Тема 5. Функции нескольких переменных.
- •Задание 5.4
- •Тема 6. Двойные и тройные интегралы.
- •Тема 7. Криволинейные и поверхностные интегралы.
- •Введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Задание 1.6
- •Тема 2. Дифференцирование функции одной переменной. Исследование функций с помощью производных. Задание 2.1
- •Задание 2.2
- •Задание 2.3
- •Задание 2.4
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Задание 3.2
- •Задание 3.3
- •Задание 3.4
- •Задание 3.5
- •Задание 3.6
- •Задание 3.7
- •Задание 3.8
- •Тема 4. Числовые и степенные ряды. Задание 4.1
- •Задание 4.6
- •Функции нескольких переменных
- •Тема 5. Функции нескольких переменных. Задание 5.1
- •Задание 5.2
- •Задание 5.3
- •Задание 5.4
- •Тема 6. Двойные и тройные интегралы.
- •КРиволинейные и поверхностные интегралы
- •Тема 7. Криволинейные и поверхностные интегралы. Задание 7.1
- •Задание 7.2
- •Список учебной литературы
Тема 6. Двойные и тройные интегралы.
Задание 6.1
Изменить порядок интегрирования:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 6.2
Вычислить объем тела, ограниченного заданными поверхностями.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 6.3
Вычислить площадь плоской области D, ограниченной заданными линиями.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 6.4
Вычислить тройной интеграл по области V, ограниченной заданными поверхностями.
1.
![]() ,
,
![]()
2.
![]() ,
,
![]()
3.
![]() ,
,
![]()
4.
![]() ,
,
![]()
5.
,
![]()
6.
![]() ,
,
![]()
7.
![]() ,
,
![]()
8.
![]() ,
,
![]()
9.
![]() ,
,
![]()
10.
![]() ,
,
![]()
11.
![]() ,
,
![]()
12.
,
![]()
13.
,
![]()
14.
![]() ,
,
![]()
15.
![]() ,
,
![]()
16.
![]() ,
,
![]()
17.
,
![]()
18.
![]() ,
,
![]()
Задание 6.5
С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КРиволинейные и поверхностные интегралы
Тема 7. Криволинейные и поверхностные интегралы. Задание 7.1
Вычислить криволинейный интеграл вдоль заданной дуги L.
1.
![]() ,
,![]() - отрезок прямой, заключенный между
точками
- отрезок прямой, заключенный между
точками
![]()
2.
![]()
![]() -
первый лепесток лемнискаты Бернулли
-
первый лепесток лемнискаты Бернулли
![]()
3.
![]() -
первый виток винтовой линии
-
первый виток винтовой линии
![]()
4.
![]()
![]() отрезок прямой, заключенный между
точками
отрезок прямой, заключенный между
точками
![]() и
и
![]()
5.
![]()
![]() -
контур треугольника с вершинами
-
контур треугольника с вершинами
![]()
6.
![]()
![]() от точки
от точки
![]() до
точки
до
точки
![]()
7.
![]()
![]()
![]()
8.
![]()
![]() от
точки
от
точки
![]() до
точки
до
точки
![]()
9.
![]()
![]() от
точки
до точки
от
точки
до точки
![]()
10.
![]()
![]() от
точки
от
точки
![]() до точки
до точки
11.
![]()
![]() -отрезок прямой, заключенный между
точками
-отрезок прямой, заключенный между
точками
![]() и
и
![]()
12.
![]() -
окружность
-
окружность
![]()
13.
![]()
![]() дуга
кривой
дуга
кривой
![]() от
точки
от
точки
![]() до
точки
до
точки
![]()
14.
![]() -
дуга окружности
-
дуга окружности
![]()
15.
![]() -эллипс
-эллипс
![]()
16.
![]()
![]() от
точки
до
точки
от
точки
до
точки
17.
![]()
![]() отрезок
прямой, соединяющий точки
и
отрезок
прямой, соединяющий точки
и
![]()
18.
![]()
![]() от
точки
до
точки
от
точки
до
точки
![]()
Задание 7.2
Вычислить поверхностный интеграл второго ряда:
1.
![]() где S-
верхняя часть плоскости
где S-
верхняя часть плоскости
![]() отсеченной
координатными плоскостями.
отсеченной
координатными плоскостями.
2.
![]() где S-
внешняя сторона нижней половины сферы
где S-
внешняя сторона нижней половины сферы
![]()
3.
![]() где S-
внешняя сторона сферы
где S-
внешняя сторона сферы
![]() лежащая
в первом октанте.
лежащая
в первом октанте.
4.
![]() где S-
верхняя сторона плоскости
где S-
верхняя сторона плоскости
![]() отсеченной координатными плоскостями.
отсеченной координатными плоскостями.
5.
![]() где S-
верхняя сторона поверхности куба,
ограниченного плоскостями
где S-
верхняя сторона поверхности куба,
ограниченного плоскостями
![]()
6.
![]() где S-внешняя
сторона поверхности сферы
где S-внешняя
сторона поверхности сферы
![]()
7.
![]() где S-внешняя
сторона сферы
где S-внешняя
сторона сферы
![]()
8.
![]() где S-
часть поверхности параболоида
где S-
часть поверхности параболоида
![]() (нормальный вектор
(нормальный вектор
![]() который образует острый угол с ортом
который образует острый угол с ортом
![]() ),
отсеченная плоскостью x=0.
),
отсеченная плоскостью x=0.
9.
![]() где S-
наружная поверхность цилиндра
где S-
наружная поверхность цилиндра
![]() отсеченная
плоскостями
отсеченная
плоскостями
![]() .
.
10.
![]() где S-
часть поверхности параболоида
где S-
часть поверхности параболоида
![]() (нормальный вектор
которой образует тупой угол с ортом
(нормальный вектор
которой образует тупой угол с ортом
![]() ),
вырезаемая цилиндром
),
вырезаемая цилиндром
![]()
11.
![]() где
S-внешняя
сторона сферы
где
S-внешняя
сторона сферы
![]() лежащая
в первом октанте.
лежащая
в первом октанте.
12.
![]() где S-
часть поверхности конуса
где S-
часть поверхности конуса
![]() (нормальный вектор
которой образует тупой угол с ортом
),
лежащая между плоскостями
(нормальный вектор
которой образует тупой угол с ортом
),
лежащая между плоскостями
![]()
13.
![]() где S-
часть поверхности параболоида
(нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостью
где S-
часть поверхности параболоида
(нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостью
![]()
14.
![]() где S-
часть поверхности гиперболоида
где S-
часть поверхности гиперболоида
![]() (нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостями
(нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостями![]()
15.
![]() где S-
верхняя сторона поверхности эллипсоида
где S-
верхняя сторона поверхности эллипсоида
![]()
16.
![]() где S-
часть поверхности параболоида
(нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостью
где S-
часть поверхности параболоида
(нормальный вектор
которой образует тупой угол с ортом
),
отсекаемая плоскостью
![]()
17.
![]() где S-
часть поверхности конуса
(нормальный вектор
которой образует острый угол с ортом
),
отсекаемая плоскостями
где S-
часть поверхности конуса
(нормальный вектор
которой образует острый угол с ортом
),
отсекаемая плоскостями
![]()
18.
![]() где S-
часть поверхности параболоида
где S-
часть поверхности параболоида
![]() (нормальный вектор
которой образует острый угол с ортом
),
отсекаемая плоскостью
(нормальный вектор
которой образует острый угол с ортом
),
отсекаемая плоскостью
![]()