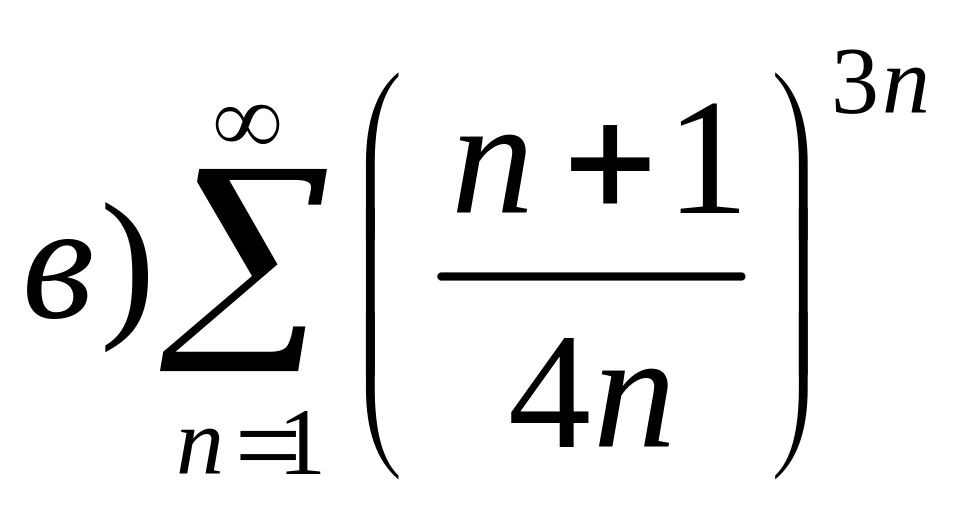- •Содержание
- •ВВеДение
- •I.Требования к оформлению контрольных работ
- •II.Формирование заданий для контрольных работ
- •Іiі. Теоретическое содержание курса «Математический анализ» введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Тема 2. Дифференцирование функции одной переменной. Исследование функций с помощью производных.
- •Неопределенный интеграл. Определенный интеграл и его приложения.
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Тема 4. Числовые и степенные ряды.
- •Функции нескольких переменных
- •Тема 5. Функции нескольких переменных.
- •Кратные интегралы
- •Тема 6. Двойные и тройные интегралы.
- •КРиволинейные и поверхностные интегралы
- •Тема 7. Криволинейные и поверхностные интегралы.
- •Іv. Решение типовых заданий введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Задание 1.6
- •Тема 2. Дифференцирование функций одной переменной. Исследование функций с помощью производных.
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Тема 4. Числовые и степенные ряды. Задание 4.1
- •Задание 4.2
- •Задание 4.3
- •Задание 4.4
- •Задание 4.5
- •Тема 5. Функции нескольких переменных.
- •Задание 5.4
- •Тема 6. Двойные и тройные интегралы.
- •Тема 7. Криволинейные и поверхностные интегралы.
- •Введение в математический анализ. Предел, непрерывность и дифференцируемость функций.
- •Тема 1. Предел функции. Непрерывность функции.
- •Задание 1.6
- •Тема 2. Дифференцирование функции одной переменной. Исследование функций с помощью производных. Задание 2.1
- •Задание 2.2
- •Задание 2.3
- •Задание 2.4
- •Тема 3 . Неопределенный интеграл. Определенный интеграл. Приложения определенных интегралов.
- •Задание 3.2
- •Задание 3.3
- •Задание 3.4
- •Задание 3.5
- •Задание 3.6
- •Задание 3.7
- •Задание 3.8
- •Тема 4. Числовые и степенные ряды. Задание 4.1
- •Задание 4.6
- •Функции нескольких переменных
- •Тема 5. Функции нескольких переменных. Задание 5.1
- •Задание 5.2
- •Задание 5.3
- •Задание 5.4
- •Тема 6. Двойные и тройные интегралы.
- •КРиволинейные и поверхностные интегралы
- •Тема 7. Криволинейные и поверхностные интегралы. Задание 7.1
- •Задание 7.2
- •Список учебной литературы
Задание 3.8
Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РЯДЫ.
Тема 4. Числовые и степенные ряды. Задание 4.1
Исследовать на сходимость числовой ряд.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4.2
Исследовать на абсолютную и условную сходимость знакочередующийся ряд:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4.3
Найти область сходимости степенного ряда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4.4
Разложить данную
функцию в ряд Тейлора в окрестности
точки
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4.5
Вычислить приближенно
с помощью рядов с заданной точностью
![]() :
:
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|
|
|
а)
|
б)
|
|
а)
|
б)
|