5. Расчет эффективной длины пластины для типового головного обтекателя в соответствии с гипотезой Авдуевского [2].

R X₃ Х X₄

X₂ Х

X

X₁ R

2 0⁰ 30⁰ R₁ R₂ R₃ R₄

O₂₀ O₃₀ O 1 Sсф 2 3 4

Рис. 5.1. Схема расчета для типового ГО

Любой точке на поверхности осесимметричного тела можно поставить в соответствие пластину, длиной Хэфф, тепловой поток на конце которой будет в точности равен тепловому потоку на поверхности тела (гипотеза Авдуевского).

Для расчет эффективной длины пластины поверхность осесимметричного тела ( в данном случае головного обтекателя) следует разбить на отдельные характерные участки: О1-сфера; 12-первый конус, 23- второй конус, 34-цилиндр.

1. Сфера: Х_эфф = 4/13 S_сф∙(π/3)R_сф

2. Рассмотрим точку Х на коническом участке 12: R=Хsin30⁰, после продления линии конуса 30⁰ пересечение с осью симметрии происходит в точке О₃₀, при этом Х₁= О₃₀Х₁, Х== О₃₀Х.

Поскольку в точке Х₁ происходит плавное сопряжение сферы и конуса 30⁰, ( =

3. Рассмотрим точку Х на коническом участке 23: R=Хsin20⁰, после продления линии конуса 20⁰ пересечение с осью симметрии происходит в точке О₂₀. при этом Х₂= О₂₀Х₂, Х== О₂₀Х.

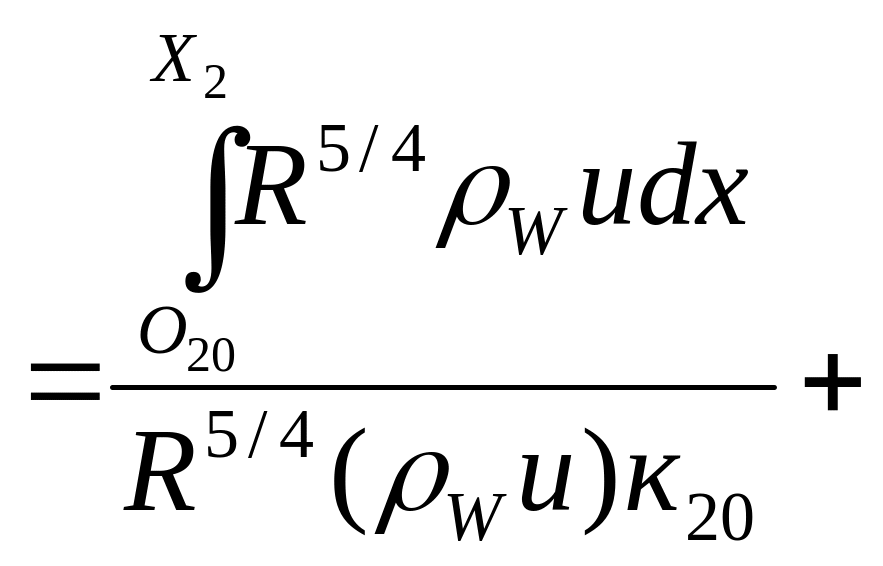
Поскольку в точке Х₂ происходит резкий переход от конуса 30⁰ к конусу 20⁰, ( 

4. Рассмотрим точку Х на цилиндрическом участке 34, на всем участке R=const.

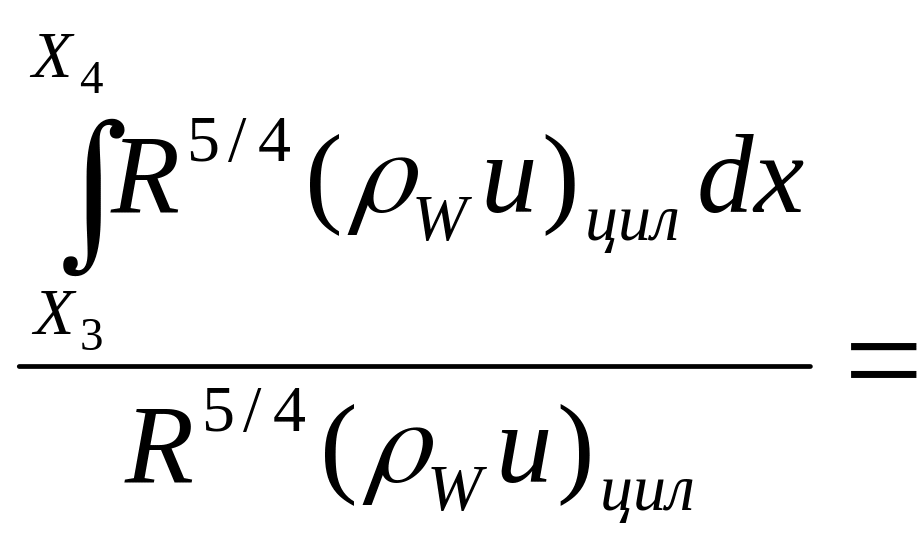
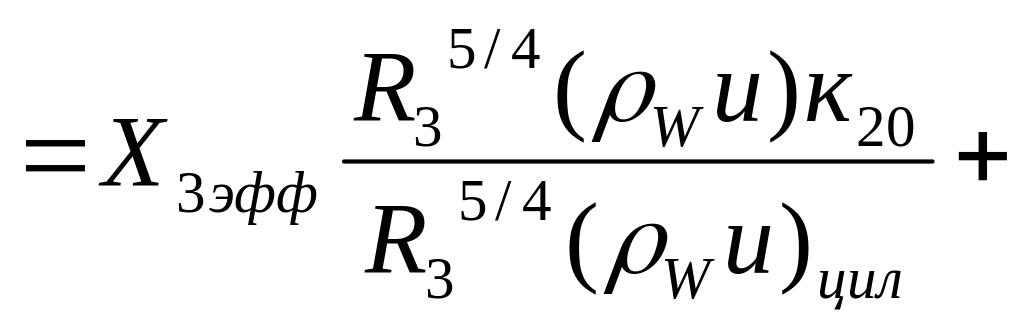
Поскольку в точке Х₃ происходит резкий переход от конуса 20⁰ к цилиндру, ( 

6. Элементы термодинамики, используемые в уравнениях, описывающих течения газа и теплообмен газа с обтекаемой стенкой.

6.1. Понятие теплоемкости, доказательство закона Роберта-Майера [7].

Теплоемкостью тела С называется отношение бесконечно малого количества тепла Q , полученного телом, к соответствующему приращению dT его температуры:

C = Q/dT (1)

Следует отметить, что для адиабатического процесса С = 0, для изотермического процесса С = ∞.

Особое значение имеют теплоемкости при постоянном объеме и при постоянном давлении сv и cp.

Используя первый закон термодинамики, запишем:

СdT = dЕ+PdV (2)

или

(3)

Пусть внутренняя энергия Е = Е (Р,V,Т), то есть является функцией давления Р, объема V и температуры Т. Но известно, что для моля вещества можно воспользоваться уравнением состояния Клапейрона, согласно которому

(4)

Поэтому верно, что внутренняя энергия зависит только от двух независимых величин, например от объема и температуры Е = Е (V,Т). Тогда

(5)

Подставляя соотношение (5) в уравнение (3), получим выражение для теплоемкости:

=

(6)

При постоянном объеме dV=0 С_V =  Е/T_V (7)

Если же постоянно давление Р=const, с учетом (7) уравнение (6) можно переписать в виде

(8)

При постоянном давлении отношение dV/dT переходит в частную производную V/T_P или из уравнения (4)

(9)

Уравнение (8) с применением (9) перепишется в следующем виде

(10)

При постоянных величинах Р и Т согласно уравнению (4), сохраняется постоянным и объем V, поэтому произведение частных производных в этом процессе равно нулю. Последнее утверждение в более общем виде, не только для изобарических процессов, было получено еще и эмпирическим путем Джоулем, который сформулировал этот опытный факт в качестве одного из основных законов термодинамики

=0 (11)

или: внутренняя энергия идеального газа есть функция только температуры.