Приклади

Використовуючи правило Лопіталя, знайти границі:

а) ; б) ; в) ;

г) ; д) ; е) .

Розв’язання. а) Маємо невизначеність вигляду . Використовуючи правло Лопіталя (формулу (4.11)), одержимо:

.

б) Також маємо невизначеність вигляду . Використовуючи правло Лопіталя тричі, одержимо:

.

в) Маємо невизначеність вигляду . Розкриваючи її за правилом Лопіталя, одержимо:

.

г) Маємо невизначеність вигляду 0. Зведемо її до невизначеності вигляду , а потім використаємо правило Лопіталя:

.

д) Маємо невизначеність вигляду –. Зведемо її до невизначеності вигляду , а потім використаємо правило Лопіталя:

= = = = .

е) Маємо невизначеність вигляду 1^.

= .

Знайдемо . Маємо невизначеність вигляду 0. Зведемо її до невизначеності вигляду , а потім використаємо правило Лопіталя та границю :

= =

= .

Отже, = .

Завдання для самостійного розв’язування

1. Використовуючи правило Лопіталя, знайти границі:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) .

Відповіді: 1. 1) ; 2) 2; 3) ; 4) +; 5) 0; 6) ; 7) .

§4.4. Застосування похідної до дослідження функцій

Зростання і спадання функції. Інтервал (a;b) називають інтервалом зростання (спадання) функції y=f(x), якщо на цьому інтервалі функція f зростає (спадає), тоді як на будь-якому ширшому інтервалі вона вже не є зростаючою (не є спадною). Наприклад, для функція f(x)=х² інтервал зростання – (0;+), а інтервал спадання – (–;0).

Знаходження інтервалів зростання і спадання за допомогою похідної грунтується на такій теоремі.

Достатня умова зростання (спадання) функції. Якщо ( ) для всіх х з інтервалу (а;b), то на цьому інтервалі функція f зростає (спадає).

Е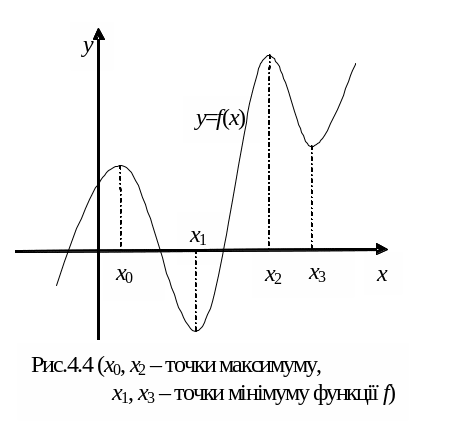 кстремуми функції. Точку х₀ називають точкою максимуму (точкою мінімуму) функції y=f(x), якщо існує окіл цієї точки такий, що для всіх х з цього околу, крім х=х₀, виконується нерівність f(x₀)>f(x) (f(x₀)<f(x)) (рис.4.4). Функція може мати декілька точок максимуму і мінімуму, а може не мати жодної.

Точки максимуму і точки мінімуму функції f називають точками екстремуму цієї функції.

Значення функції y=f(x) у точці максимуму (точці мінімуму) називають максимумом (мінімумом) функції f. Максимум і мінімум функції f називають екстремумами цієї функції.

Необхідна умова існування точки екстремуму функції (теорема Ферма). Якщо х₀ – точка екстремуму функції f, то =0 або функція f не є диференційованою у точці x₀ ( = або не існує).

Точки з області визначення функції f, в яких дорівнює нулю або нескінченності, або не існує, називають критичними точками функції f.

Враховуючи це означення теорему Ферма можна сформулювати так: якщо х₀ – точка екстремуму функції f, то ця точка є критичною точкою функції f.

Теорема Ферма стверджує, що точки екстремуму функції містяться серед її критичних точок. Але не кожна критична точка функції є точкою екстремуму цієї функції. Виділити точки екстремуму серед її критичних точок допомагає достатня умова існування точки екстремуму функції.

Достатня умова існування точки екстремуму функції. Нехай функція диференційована в околі критичної точки x₀, за винятком, можливо, самої точки x₀, в якій функція f неперервна. Тоді: 1) якщо при переході точки x через точку x₀ змінює знак з “+” на “–”, то точка x₀ є точкою максимуму функції f, а якщо – з“–” на “+”, то точка x₀ є точкою мінімуму функції f; 2) якщо при переході точки x через точку x₀ не змінює знаку, то x₀ не є точкою екстремуму функції f.