
Заняття 8 Модуль ііі. Вступ до математичного аналізу
§3.1. Функції та їх основні властивості. Елементарні функції
Нехай задано множини Х і Y. Якщо кожному елементу хХ за певним законом поставлено у відповідність єдиний елемент yY, то кажуть, що на множині Х задана (визначена) функція, і записують y=f(x), хХ. При цьому елемент х називають аргументом функції f, а елемент y – значенням функції f в точці х.
Множину Х називають областю визначення функції f і позначають D(f), а множину всіх елементів yY, для яких y=f(x), хХ, – множиною значень функції f і позначають Е(f).
Якщо елементами множин Х і Y є дійсні числа, то функцію f називають числовою. Надалі розглядатимемо лише числові функції.
Графіком функції y=f(x) називають множину точок (x; f(x)) площини XOY, де хD(f).
Основні способи задання функції:
аналітичний (за допомогою однієї або кількох формул);
графічний (за допомогою лінії, що є графіком функції);
табличний (за допомогою таблиці, в якій зазначено певні значення аргументу та відповідні значення функції).
Іноді функцію задають за допомогою формули і не вказують її область визначення. У цьому випадку під областю визначення функції розуміють множину всіх значень аргументу, при яких задана формула має зміст.
Складена функція.
Нехай функція
y=f(t)
визначена на множині Е,
а функція t=g(x)
на множині Е1,
причому для кожного значення хЕ1
відповідне значення g(x)=t
належить множині Е.
Тоді на множині Е1
визначена функція
![]() ,
яку називають складеною
функцією від змінної х,
або суперпозицією
(композицією)
функцій f і
g. При цьому
функцію f
називають зовнішньою,
а g
– внутрішньою
функцією складеної функції
.
Наприклад, функція y=sin
t
визначена на множині R
усіх дійсних чисел, а функція
,
яку називають складеною
функцією від змінної х,
або суперпозицією
(композицією)
функцій f і
g. При цьому
функцію f
називають зовнішньою,
а g
– внутрішньою
функцією складеної функції
.
Наприклад, функція y=sin
t
визначена на множині R
усіх дійсних чисел, а функція
![]() визначена на інтервалі
визначена на інтервалі
![]() .
Тоді суперпозиція цих функцій
.
Тоді суперпозиція цих функцій
![]() є складена функція від х,
визначена на інтервалі
.
є складена функція від х,
визначена на інтервалі
.
Обернена функція.
Нехай задано функцію
y=f(x),
причому будь-яким двом різним елементам
x1,
x2D(f)
функція f
ставить у відповідність два різних
елементи y1,
y2E(f).
Тоді можна говорити про функцію, яка
кожному елементу yE(f)
ставить у відповідність єдиний елемент
xD(f).
Таку функцію називають оберненою
до функції f
і позначають f –1.
Зауважимо, що не для всіх функцій існують
обернені. Наприклад, для функції
![]() ,
хR
обернена функція не існує, бо різним
значенням x1
і x2
можуть відповідати однакові значення
y1
і y2
(y1=y2).
Так, якщо x1=2,
x2=–2
(x1x2),
то y1=y2=4.
Однак, якщо розглянути функцію
,
х[0;+),
то для неї існує обернена функція, яка
визначається формулою
,
хR
обернена функція не існує, бо різним
значенням x1
і x2
можуть відповідати однакові значення
y1
і y2
(y1=y2).
Так, якщо x1=2,
x2=–2
(x1x2),
то y1=y2=4.
Однак, якщо розглянути функцію
,
х[0;+),
то для неї існує обернена функція, яка
визначається формулою
![]() .
.
Для того щоб знайти функцію, обернену до функції y=f(x), потрібно розв’язати рівняння y=f(x) відносно х і поміняти місцями х і y.
Властивості функцій
Парні (непарні)
функції.
Функцію
y=f(x)
називають парною
(непарною),
якщо для будь-якого хD(f)
виконуються умови: 1) (–х)D(f);
2)![]() (
(![]() ).
Перша умова означає, що область визначення
парної (непарної) функції є множиною,
симетричною відносно точки х=0.
).
Перша умова означає, що область визначення
парної (непарної) функції є множиною,
симетричною відносно точки х=0.
Наприклад, функція
![]() є парною, а функція
є парною, а функція
![]() – непарною. Справді, область визначення
кожної з них (це множина R
усіх дійсних чисел) симетрична відносно
точки х=0
і для будь-якого х
виконуються рівності:
– непарною. Справді, область визначення
кожної з них (це множина R
усіх дійсних чисел) симетрична відносно
точки х=0
і для будь-якого х
виконуються рівності:
![]() ,
,
![]() .
.
Серед тригонометричних
функцій парною є функція
![]() ,
а непарними –
,
а непарними –
![]() ,
,
![]() ,
,
![]() .
.
Графік парної функції симетричний відносно осі ординат, а графік непарної – відносно початку координат (рис.3.1).
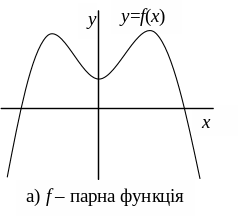

Рис. 3.1
