Заняття 5

Модуль 2 АНАЛІТИЧНА ГЕОМЕТРІЯ

АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ

§ 2.1. Прямокутна система координат на площині

Аналітична геометрія – область математики, яка вивчає геометричні образи алгебраїчними методами. Для цього ці геометричні образи розглядаються у деякій системі координат, яка визначає лінійний векторний простір. Одна із найпростіших систем є декартова прямокутна система координат. На площині така система координат задається двома взаємно перпендикулярними осями та , що мають спільний початок і однакову масштабну одиницю. Вісь називають віссю абсцис, в вісь – віссю ординат, точка перетину осей – початком координат.

Рис. 1.

Будь-яка точка на площині характеризується єдиною парою чисел (вектором) . І навпаки будь-яка пара чисел (будь-який вектор) визначає на площині єдину точку. Таку пару чисел називають координатами точки . Перше число цієї пари називають абсцисою точки, а друге – ординатою. Початок координат має координати .

Відстань між точками визначається рівністю

(1)

Площа трикутника, вершинами якого є три точки , , , визначається за формулою:

. (2)

Поділ відрізка у пропорційному відношенні. Нехай координатами кінців відрізка є . Тоді координати точки , для якої справедливе співвідношення , визначається рівностями:

. (3)

Якщо ж точка ділить відрізок навпіл, то і координати точки, що є серединою відрізка матимуть вигляд .

Приклади.

1. Знайти площу трикутника, вершини якого мають такі координати: .

Розв'язання. Згідно формули (2) маємо:

.

2. Знайти точку , яка у два рази ближче до точки , ніж до точки .

Розв'язання. Точка ділить відрізок у відношенні . Використовуючи формулу (5) маємо:

.

Завдання для самостійного розв'язання

1. Знайти координати точок, симетричних відносно початку координат, відносно осі , відносно осі точці:

2. Точка М є серединою відрізка ОА, що з'єднує початок координат з точкою . Знайти координати точки М.

3. Знайти площу трикутника АВС, якщо відомо координати його вершин: _.

Відповіді:

1. _.

2.

3. S = .

§ 2.2. Рівняння прямих на площині

Запишемо найпоширеніші види рівнянь прямої на площині.

Рівняння прямої з кутовим коефіцієнтом

, (4)

де – кутовий коефіцієнт, α – кут нахилу прямої до осі , – ордината точки перетину прямої з віссю .

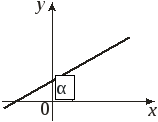
Рис. 2.

Рівняння прямої, що проходить через задану точку із заданим кутовим коефіцієнтом :

. (5)

При довільному значенні коефіцієнта це рівняння визначає жмуток прямих, що проходить через точку , крім прямої, паралельної осі , яка не має кутового коефіцієнта.

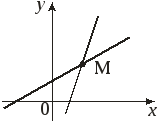
Рис. 3.

Рівняння прямої, що проходить через дві задані точки та :

. (6)

Рис. 4.

Рівняння прямої, що проходить через задану точку і має відомий вектор напряму :

. (7)

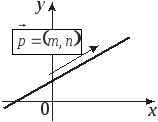
Рис. 5.

Параметричне рівняння прямої

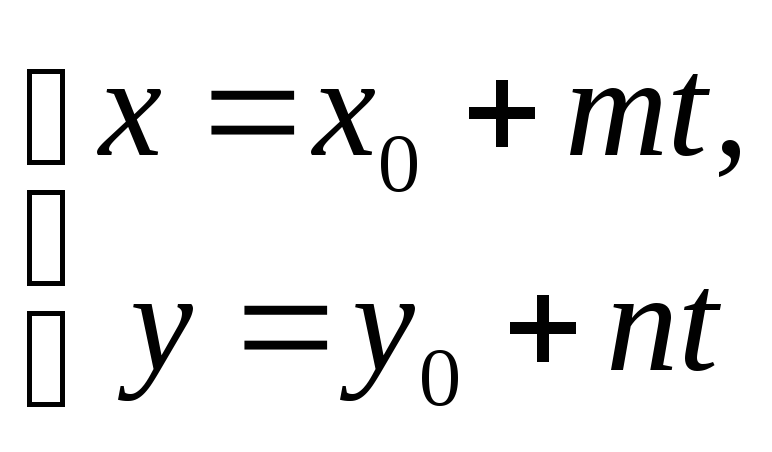. (8)

Рівняння прямої у відрізках.

, (9)

де – абсциса точки перетину прямої з віссю ; – ординати точки перетину прямої з віссю .

Загальне рівняння прямої:

, (10)

де А, В, С – довільні коефіцієнти (А і В одночасно не дорівнюють нулю). Коефіцієнти А і В є також координатами вектора перпендикулярного до прямої (вектора нормалі прямої).

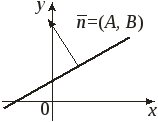
Рис. 6.

Загальне рівняння прямої, що проходить через задану точку матиме вигляд:

. (11)

Частинні випадки загального рівняння.

1. При С = 0, . , пряма проходить через початок координат.

2. При . , пряма паралельна осі .

3. При . , пряма паралельна осі .

4. При . пряма є віссю .

5. При . пряма є віссю .

Якщо відомі кутові коефіцієнти двох прямих і , то один із кутів між ними визначається рівністю

. (12)

Другий кут між прямими дорівнює .

Умова паралельності двох прямих: .

Умова перпендикулярності двох прямих: .

Якщо дві прямі задаються рівнянням в загальній формі

, ,

то один із кутів між цими прямими визначається кутом між двома нормалями до них: та :

. (13)

Умова паралельності двох прямих визначається умовою паралельності їхніх нормалей : , а умова перпендикулярності – умовою перпендикулярності їхніх нормалей: .

Відстань від точки до прямої знаходиться за формулою

. (14)

Приклади.

1. Скласти рівняння прямої, яка проходить через дві точки та . Записати це рівняння з кутовим коефіцієнтом.

Розв'язання. У цьому випадку маємо . Підставивши їх у рівність (16) отримаємо

, або .

Виразимо з останнього рівняння змінну через . Отримаємо рівняння прямої з кутовим коефіцієнтом .

2. Через точку провести пряму, яка:

1) паралельна осі ;

2) паралельна осі ;

3) проходить через початок координат;

4) паралельна прямій ;

5) перпендикулярна прямій .

Розв'язання. 1) Рівняння прямої, що паралельна осі , має вигляд: . Так як точка лежить на ній, то рівняння прямої має вигляд .

2) Аналогічно попередньому пункту одержуємо рівняння прямої , яка проходить через точку і паралельна осі .

3) Рівняння прямої, що проходить через початок координат має вигляд: . Із умови, що точка лежить на ній, отримуємо . Отже, рівняння прямої .

4) Рівняння прямої будемо шукати у вигляді . Із умови паралельності цієї прямої до слідує, що . Для виконання цієї пропорції достатньо взяти . Отже, рівняння прямої

.

5) Рівняння прямої будемо шукати у вигляді , нормаллю якої є вектор . Із умови перпендикулярності цієї прямої до , нормаллю якої є слідує, що . Будь-який ненульовий розв'язок цього рівняння і визначає рівняння шуканої прямої: . Отже, рівняння прямої

.

3. Через точку провести пряму під кутом 45⁰ до прямої . Знайти відстань від цієї точки до заданої прямої.

Розв'язання. Рівняння прямої, що проходить через точку будемо шукати у вигляді з кутовим коефіцієнтом . цей коефіцієнт знайдемо з умови, що пряма проведена під кутом 45⁰ до заданої з кутовим коефіцієнтом . Скориставшись формулою (11) отримаємо рівняння відносно невідомого кутового коефіцієнта : , або . Підставивши розв'язок у рівняння шуканої прямої одержимо , або .

Якщо позначити , то з формули (11) відносно невідомого кутового коефіцієнта отримаємо рівняння або . Його розв'язком є . Підставивши знайдений кутовий коефіцієнт у рівняння прямої одержимо , або .

Отже, через точку можна провести до прямої під кутом 45⁰ дві прямі: та .

4. Нехай задано вершини трикутника . Скласти рівняння сторін трикутника, висоти , опущеної на сторону та знайти координати її основи.

Розв'язання. Скористаємось формулою (6) для знаходження рівняння сторін АВ, АС, ВС:

для АВ: ;

для АС: ;

для ВС: .

Рівняння висоти трикутника, опущеної з вершини В будемо шукати у вигляді (10): . Коефіцієнти А, В знайдемо з умови перпендикулярності висоти до прямої АС. Нормаллю прямої АС є вектор , а шуканої висоти – . З умови перпендикулярності отримуємо рівняння , ненульовий розв'язок якого є . Отже рівняння висоти .

Основа висоти D лежить одночасно на висоті та на стороні АС. Тому для знаходження її координат потрібно розв'язати систему рівнянь

Знайшовши розв'язок цієї системи отримуємо координати D .

Завдання для самостійного розв'язання.

1. Привести до рівнянь з кутовим коефіцієнтом та у відрізках задане рівняння прямої і побудувати її: .

2. Знайти точку перетину висот трикутника, якщо його вершинами є точки .

3. Знайти точку перетину медіан трикутника якщо його вершинами є точки .

4. Записати рівняння сторін трикутника та знайти його внутрішній кут А, якщо вершини його задаються координатами: .

Відповіді:

1.

2. .

3. .

4. .