1. Перестановки

Перестановками из п элементов называются комбинации из п элементов, которые отличаются друг от друга порядком расположения элементов. Обозначается Pn. Формула для определения числа всех перестановок: Pn=n!

Доказательство. Первый элемент можно выбрать п способами, 2-й - (n-1) способами, 3-й (n-2) способами, последний - только одним способом. По правилу произведения Рn = n(n-1)(n-2)...1 = n!, ч.т.д.

2. Сочетания

Сочетаниями из n элементов по m элементов называются комбинации из m элементов, которые отличаются друг от друга только составом элементов.

Из определения сочетания ясно, что порядок расположения элементов внутри комбинации не имеет значения, в отличие от размещения. В данном случае мы рассматриваем неупорядоченные множества из m элементов, выбранных из n-элементного множества. Сочетания обозначаются 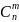. Формула для числа всех сочетаний из п по /с элементов: (1)

Доказательство. Докажем формулу: * P_m = . (2) Действительно, число всех размещений можно пересчитать следующим образом: сначала составим всевозможные сочетания; они будут отличаться только составом элементов; а затем внутри каждого сочетания проделаем всевозможные перестановки. Число этих способов по правилу произведения будет равно левой части формулы (2). Выразив из (2) сочетание , с учетом получим искомую формулу(1)

3.Размещения

Размещениями из n элементов по к элементов называются комбинации из к элементов, которые отличаются друг от друга составом элементов и/или порядком их расположения. Иными словами, размещения - это упорядоченные подмножества из к элементов, выбранные из n- элементного множества. Число размещений обозначается А_n^k (а из эн по ка).

Название «размещение» произошло от задачи: разместить к предметов в п пронумерованных ячейках. Сколько последовательностей «полненных ячеек можно получить? Например, если имеются 3 ячейки и 2 предмета А я В, то получим следующую последовательность заполненных ячеек: (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3,2). Таким образом, A₃²= 6.

Формула для числа всех размещений из n элементов по к элементов без повторений:

А_n^k = n(n -1 )(n - 2)...(n -к +1)

Доказательство. Для составления комбинации из к элементов

1 -й элемент можно выбрать n способами,

2-й элемент можно выбрать п -1 способами,

3-й элемент можно выбрать п- 2 способами,

к-й элемент можно выбрать п-(к-1)=п-к + 1 способами (мы заметили, что вычитаемое все время на единицу меньше номера элемента).

По правилу произведения всего способов п(п-1)(п-2)...(п-к + 1), ч.т.д.

4. Алгебра событий

Испытанием называется осуществление на практике какого-либо комплекса условий. В теории вероятностей изучаются только такие испытания, которые могут быть повторены, хотя бы теоретически, неограниченное число раз. В результате испытания наблюдают различные явления, которые называются событиями. События делятся на детерминированные и случайные. Детерминированными событиями называются те, которые при неоднократном повторении испытания протекают каждый раз одинаково. Случайными событиями называются события, которые могут произойти или не произойти в результате испытания по не зависящим от нас причинам. Проведению каждого испытания соответствует определенный исход - случайное событие, которое называется элементарным событием. Результатом каждого испытания является одно и только одно элементарное событие. Элементарные события обычно обозначают строчными буквами ω или е.