3.Подготовка и расчёт контрольного примера.
3.1.Исходные данные и постановка задачи.
Для условия задачи приведённой в разделе 2.1 значения величин следующие:
n = 7; C1 = 200,0; C2 = 500,0.
P(n): 0,35; 0,22; 0,16; 0,10; 0,08; 0,06; 0,03.
Требуется определить оптимальное количество запасных валов N* - такое, которое обеспечивает минимальные суммарные затраты на приобретение и убытки из-за нехватки запасных валов при поломке работающих.
3.2 Математическая модель и критерий оптимизации.
Согласно условию задачи математическая модели и критерий оптимизации будут иметь вид:
(3.1)
3.3.Решение задачи для случая дискретных значений P(n).
Согласно (2.4) и (2.9) запишем:
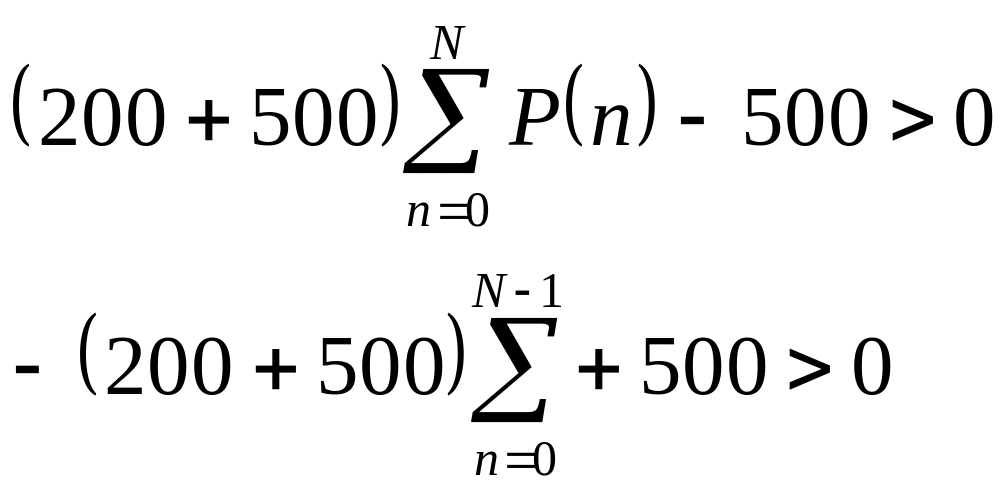(3.2)
Преобразуя (3.2) на основании (2.10) и (2.11) получим выражение (2.12) в виде:
(3.3)
Используя ряд значений P(n) определим N*:
для (N*-1): для N*=4:
P(3) = 0,714 < 0,724 < 0,814=P(4)
Оптимальное количество запасных валов N*=4.
3.4. Для случайных непрерывных величин аппроксимация ряда распределения вероятностей законом распределения вероятностей.
Построим гистограмму:
Рис. 3.1
По виду гистограммы принимаем для аппроксимации показательный закон распределения вида (2.20).
Определим его параметры:
В результате показательный закон распределения будет иметь вид
(3.4)
Выполним оценку сходимости статистического (экспериментального) и теоретического (согласно (3.4)) распределений согласно критерия Пирсона (2.24). В таблице 3.2 приведены расчитаные значения и исходные данные для оценки по критерию Пирсона – вероятностей случайной величины n.
Таблица 3.2
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
P(n) |
0 |
0.35 |
0.22 |
0.16 |
0.10 |
0.08 |
0.06 |
0.03 |
P*(n) |
0.379 |
0.259 |
0.178 |
0.122 |
0.083 |
0.057 |
0.039 |
0.027 |
(Pj*-Pj)2 |
|
0.0083 |
0.0018 |
0.0014 |
0.0069 |
0.0005 |
0.0004 |
0.00001 |
Вычисленное значение
число степеней свободы:
k=S-3=7-3=4
где S – число значений xi=7
уровень
значимости принимаем
По
таблице значения вероятностей
определим
0,9098
В
результате, так как
то гипотеза о принятом распределении
- экспоненциальном принимается :
Далее определим (для N=7):
Анализируя исходный ряд значений P(n) находим, что ближайшие значения вероятности P(n)=0,714 будет при n=N*=4. Следовательно оптимальное значение валов:
NH*=4