Математичне очікування та дисперсія розподілення Пуассона

Математичне очікування (чи середнє число „успіхів” на якому-небудь інтервалі) може бути визначено за даними конкретної ситуації.

Якщо знайдено , то і відома дисперсія , так як одна з властивостей розподілення ймовірності Пуассона є

Звідси, стандартне відхилення числа „успіхів” на інтервалі дорівнює

Дискретні розподіли

(Канонічні закони розподілу Д ВВ)

1. Біноміальний закон розподілу – ймовірність того, що подія А відбудеться х раз в n незалежних дослідах, якщо її ймовірність Р (схема Бернуллі)

2. Геометричний закон розподілу – ймовірність того, що знайдеться х дослідів, щоб відбулася подія А, якщо її ймовірність р.

3. Розподіл Паскаля – ймовірність того, що треба провести х дослідів, щоб подія А з ймовірністю р здійснилася s разів.

4. Розподіл Пуассона – ймовірність появи х незалежних подій на інтервалі часу 0, ..., t, якщо події проходять з постійною інтенсивністю .

е^-1 0,37; е^-2 1/7; е^-3 1/20; е^-4 1/50.

Лекція

Тема: Неперервні випадкові величини.

Означення. Неперервною випадковою величиною – називається така випадкова величина Х – яка в результаті дослідів може набувати будь-яке значення в одному чи декількох заданих інтервалах.

Приклад. Відстань на мішені від 9 до точки влучення в мішень.

det. Функція F(x_i), яка дорівнює ймовірності того, що випадкова величина Х прийме значення не більше x_i тобто – називається функцією розподілення або інтегральною функцією розподілу.

Властивості функції розподілення f(X)

1. 

2. 

3. 

4. 

5. 

6. 

Неперервну випадкову величину можна також задати, використовуючи іншу функцію, яку називають щільністю ймовірності (чи диференційною функцією).

Ймовірність попадання неперервної випадкової величини в заданий інтервал

Знаючи щільність розподілення, можна обчислити ймовірність того, що неперервна випадкова величина приймає значення, яке належить заданому інтервалу.

Теорема Ймовірність того, що неперервна ВВ Х приймає значення, яке належить інтервалу [а, b], дорівнює визначеному інтервалу від щільності розподілення, взятому в межах від а до b.

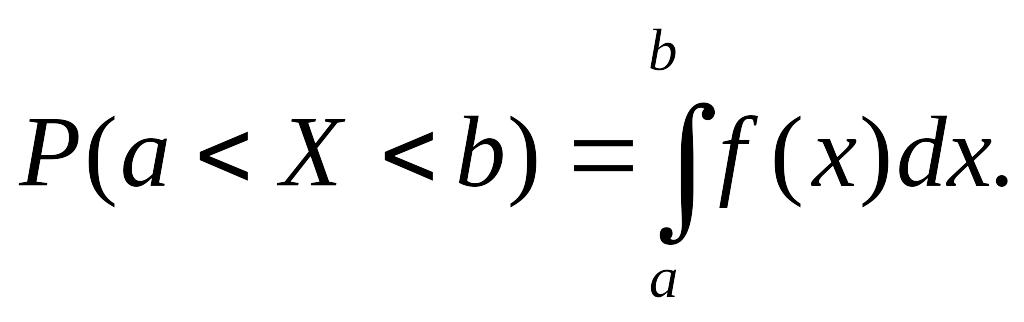
Доведення.

Використовуючи співвідношення

За формулою Ньютона – Лейбніца

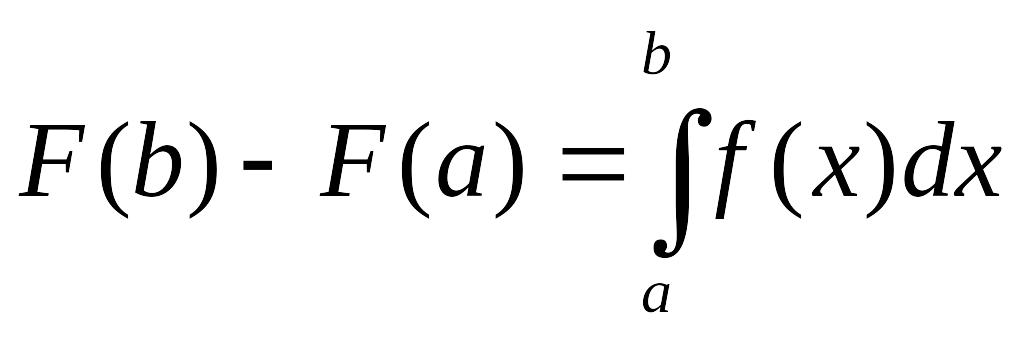
Таким чином

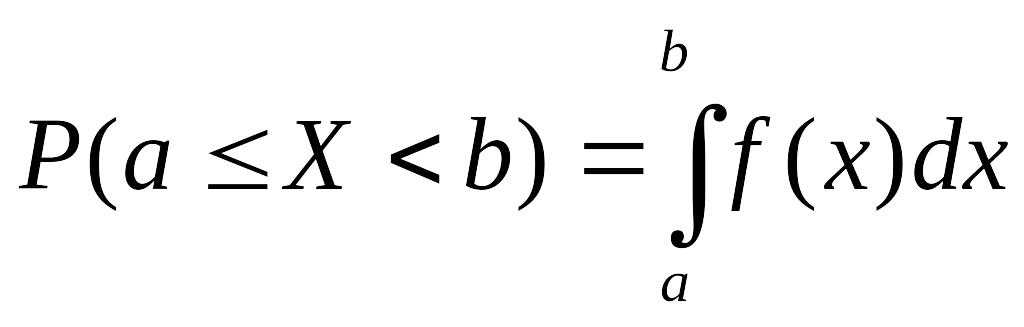
Так як , то отримаємо

Приклад. Задана щільність ймовірності ВВ Х

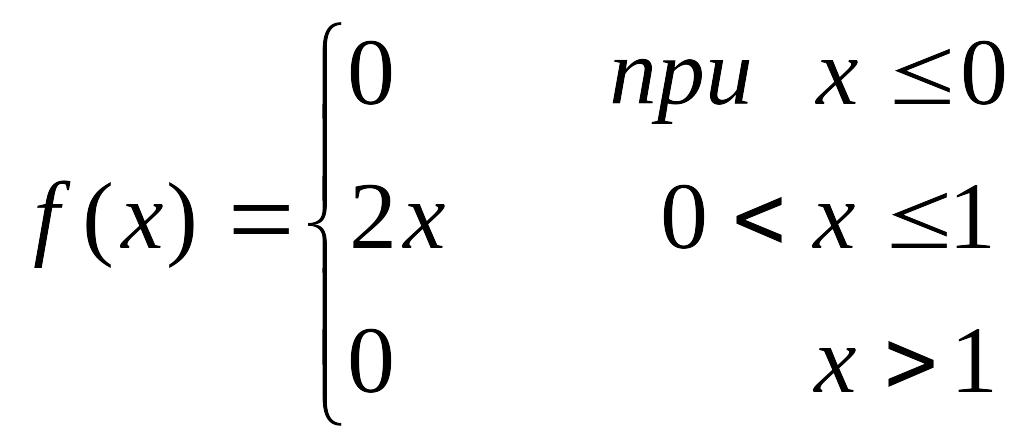
Знайти ймовірність того, що в результаті досліджень Х приймає значення, яке належить інтервалу (0,5; 1).

Імовірнісний зміст щільності розподілення

Нехай – деяке дійсне число. Розглянемо ймовірність нерівності

– довжина малого інтервалу.

Означення. Функція – це є щільність неперервного розподілу ймовірності. За означенням похідної, очевидно, що (диференціальна функція розподілу)

З врахуванням цього маємо:

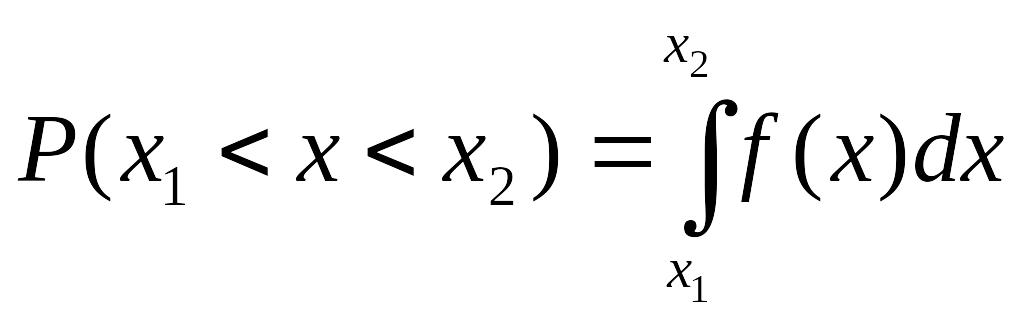
З цих співвідношень випливає, що площа під кривою диференціальної функції розподілу дорівнює 1.

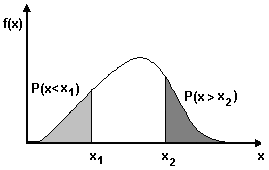
Графік щільності розподілення , де площа заштрихованих участків дорівнює ймовірності того, що чи

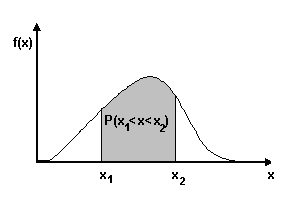
Це геометрично імовірнісне попадання величини Х на відрізок ( ) дорівнює площині кривої розподілення, яка опирається на цей відрізок.

Таблиця частот

(№ ****)	(частота)
1	2
2	3
3	1
4	1
5	1

Гістограма (графік частот)

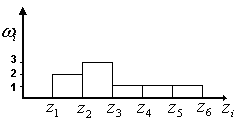
Це дискретний аналіз функції щільності ймовірності.

По гістограмі можна сказати, що робота автомата зміщена вліво.

Нехай при статистичному досліджені випадкової величини в генеральній сукупності на основі вибірки (х₁, х₂, ..., х_n) необхідно оцінити математичне сподівання .

Вибіркове середнє .

Оцінка математичного сподівання

Вибіркова дисперсія

– зміщена оцінка