4. Минимизация логических функций трех переменных с помощью диаграмм Вейча

Цель занятия: Приобретение навыков минимизации функций включения трех переменных при синтезе автоматических устройств.

Методика выполнения задания

1. Если исходная функция представлена в ДНФ (КНФ), то следует в начале составить Карно (диаграмму Вейча), в которой число клеток равно возможных минтермов (при n = 3, число входных наборов равно 2 = 8), далее, как в предыдущем задании, заполняют клетки нулями и единицами в определенном порядке, характерном для случая n = 3, что схематично показано ниже.

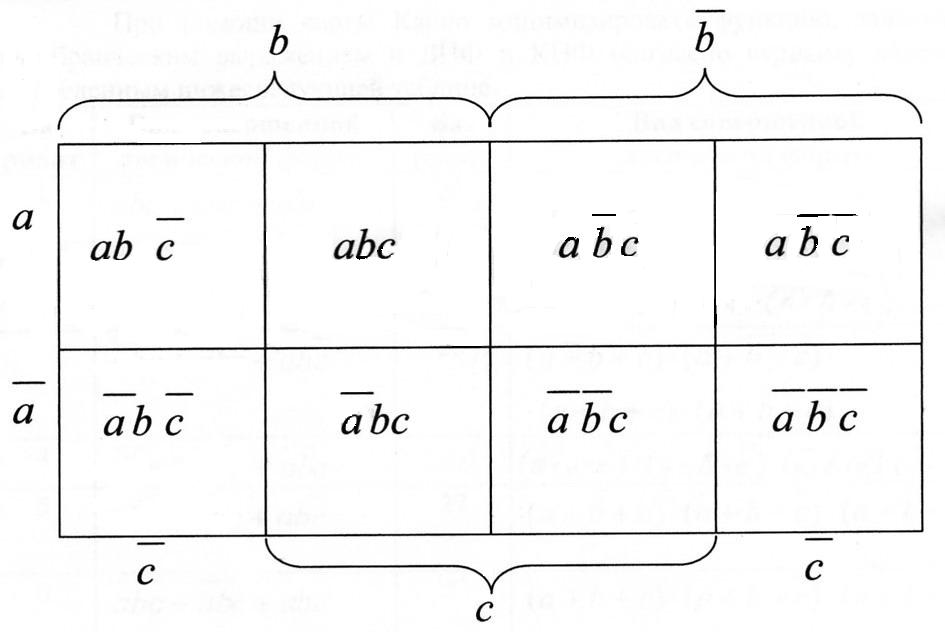
2. После того, как прямоугольная таблица Вейча заполнена 0 и 1, обводят прямоугольными контурами либо все единицы при заданной функции в ДНФ и затем записывают минимизированную функцию в виде суммы логических произведений, описывающих эти контуры, либо все нули (если КНФ) и затем записывают минимизированную функцию в виде произведения логических сумм, описывающих эти контуры. Причем в контуре могут одновременно содержаться 1, 2, 4, 8 клеток.

Правила исключения входных переменных из рассмотрения при минимизации функции n = 3. Так же, что и при n = 2.

3. Если исходная функция представлена таблицей истинности, то вначале записывают логическую функцию в ДНФ или КНФ (в зависимости от варианта задачи) и заполняют прямоугольную таблицу нулями и единицами аналогично предыдущему заданию по приведенной ниже схеме заполнения для n = 3. Далее минимизация осуществляется в том же порядке, что и пункт 2 настоящей методики.

Задание № 1 При помощи карты Карно минимизировать функцию, заданную таблицей истинности для n = 3, приведенной в лабораторно – практической работе № 3.

Задание № 2 При помощи карты Карно минимизировать функцию, заданную алгебраическим выражением в ДНФ и КНФ (согласно варианту задачи), приведенным нижеследующей таблице.

Ва- риант	Вид совершенной логической формы	Ва- риант	Вид совершенной логической формы
1		17
2		18
3		19
4		20
5		21
6		22
7		23
8		24
9		25
10		26
11		27
12		28
13		29
14		30
15		31
16		32

Пример выполнения задания №1

Минимизировать функцию трех переменных с помощью карты Карно, заданную в ДНФ (КНФ).

(1)

(2)

1. Составляем карту Карно для функции, представленной уравнением (1);

2. Обводим прямоугольными контурами единицы в таблице Вейча;

3. Составляем по указанным выше правилам логическое уравнение.

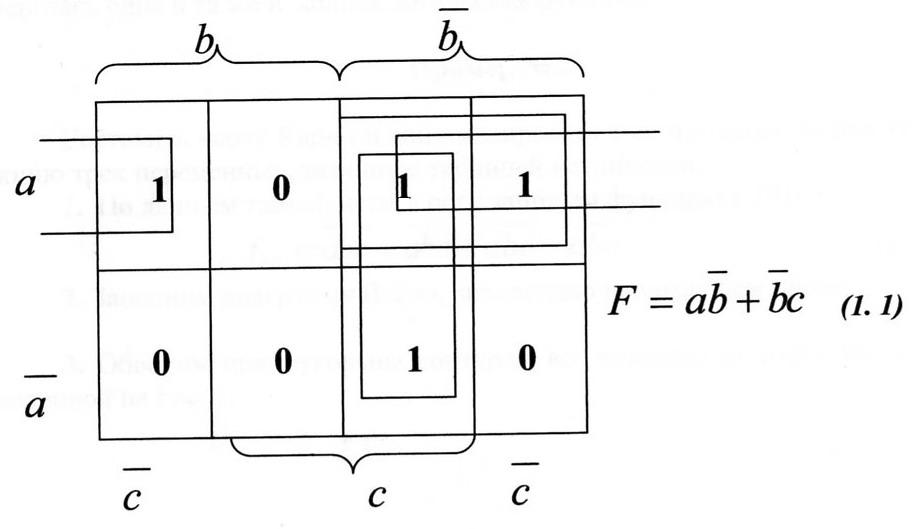
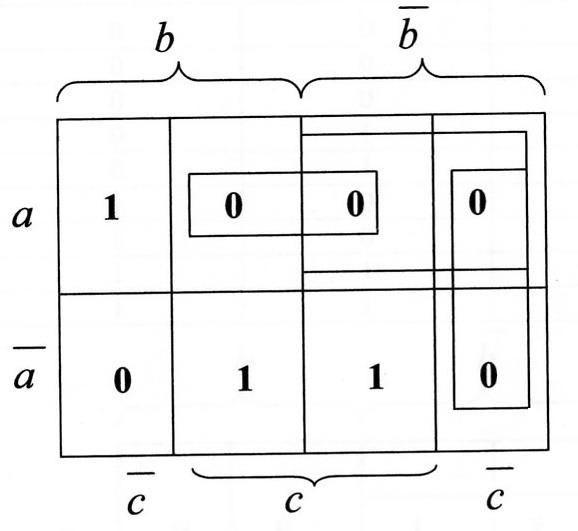
Функция (1. 1) является минимизированной функцией заданной исходным уравнением.

4. Составляем карту Карно для функции, представленной уравнением (2).

5. Обводим прямоугольными контурами нули в таблице Вейча.

6. Составляем по указанным выше правилам логическую функцию:

(2.1)

Как видим записи функции (1. 1) и (2. 1) идентичны, что указывает на правильность полученных результатов, поскольку минимизации подверглась одна и та же исходная логическая функция.