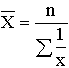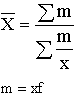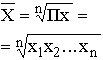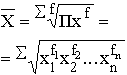1.5. Средние показатели

Средняя величина является наиболее распространенной формой статистических показателей используемой в менеджерской практике и представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимыми в анализе явлений и процессов общественной жизни.

Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности варьируют под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Сущность средней в том и заключается, что в ней взаимокомпенсируются отклонения значений признака, которые обусловлены действием случайных факторов, и накапливаются (учитываются) изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов.

Основные принципы применения средних величин.

1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.

2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.

3. Средняя должна рассчитываться для совокупности в стационарных условиях (когда влияющие факторы не меняются или меняются не значительно).

4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.

Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС), или ее логическую формулу:

. (1.8)

Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение средней. Однако от того, в каком виде представлены исходные данные, зависит, каким именно образом исходное соотношение средней будет рассчитываться.

Расчет большинства конкретных статистических показателей основан на использовании:

• средней агрегатной;

• средней степенной (гармонической, геометрической, арифметической, квадратической, кубической);

• средней хронологической (см. раздел ).

Все средние, за исключением средней агрегатной, могут рассчитываться в двух вариантах — как взвешенные или невзвешенные.

Средняя агрегатная. Используется формула:

,

где w_i=x_i*f_i;

x_i — i-й вариант осредняемого признака;

f_i, - вес i - го варианта.

Средняя степенная. В общем виде формула для расчета:

,

где степень k – вид средней степенной.

Формулы расчета степенных средних

Вид степенной средней	Показатель степени (k)	Формула расчета
		Простая	Взвешенная
Гармоническая	-1
Геометрическая	0
Арифметическая	1
Квадратическая	2
Кубическая	3

Значения средних рассчитанных на основании средних степенных для одних и тех же исходных данных - не одинаковы. С увеличением показателя степени k, увеличивается и соответствующая средняя величина:

Средняя хронологическая. Для моментного динамического ряда с равными интервалами между датами, рассчитывается по формуле:

,

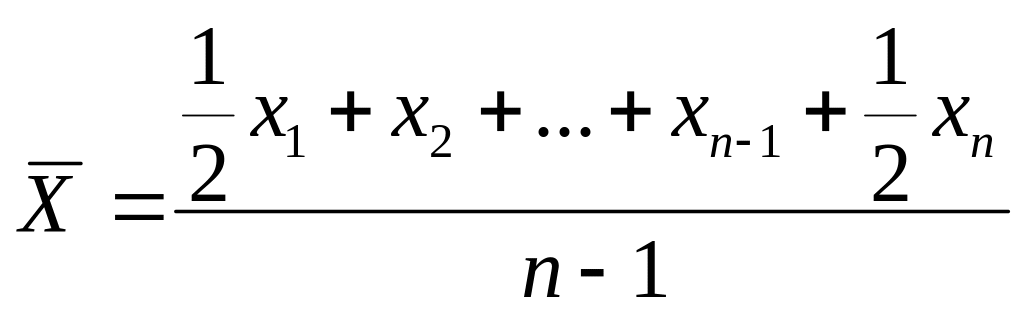где х₁ и х_n значение показателя на начальную и конечную дату.

Основные свойства средней арифметической.

1) Сумма отклонений значений признака от средней арифметической равно 0.

2) Если от каждого варианта вычесть или к каждому варианту прибавить какое-либо постоянное число, то среднее увеличится или уменьшится на тоже самое число.

3) Если каждый вариант умножить или разделить на какие-либо число, то среднее уменьшится или увеличится во столько же раз.

4) Если веса или частоты разделить или умножить на какое-либо число, то величина средней не изменится.

Это свойство даёт возможность частоты заменять их удельными весами

, где «р»- удельный вес –выраженный в процентах.

Если удельный вес выражается в доле, то Х среднее =

Особое внимание в статистике уделяется случаю, когда единицы совокупности разделены на несколько групп (см. рис. 1.4).

Рис. 1.4.

Fi—количество единиц в группе.

Среднее гармоническое рассчитывается в тех случаях, когда:

• среднее арифметическое по имеющимся данным рассчитать невозможно (см. выше);

расчет средних гармонических более удобен , где Х варианты

Формула средней гармонической взвешенной используется в тех случаях, когда значение признака и вес даны в виде сомножителя.