Приложение 2 Статистические распределения и их основные характеристики

Типы распределений

Различают дискретные и непрерывные вероятностные распределения. Дискретное распределение характеризуется тем, что оно сосредоточено в конечном или счетном числе точек. Непрерывное распределение "размазано" по некоторому вещественному интервалу.

При обработке выборочных данных, в силу случайной природы процесса получения выборки, важно знать, каким вероятностным законам подчиняются выборочные значения исследуемого экономического показателя. Существует целый ряд распределений вероятности, которые играют роль эталона в статистических выводах. Это прежде всего равномерное распределение, нормальное распределение (распределение Гаусса) и распределение Стьюдента (t-распределение).

Общие принципы представление законов распределения случайной величины

В общем случае, разбивая интервал значений непрерывной величины ( , х₂,) на два интервала ( , х₁,) и (х₁ х₂) (одновременные попадания случайной величины в которые являются взаимоисключающими событиями), получаем:

Рrоb{ ≤Х< x₁} + Рrоb{х₁ ≤Х< х₂,} = Рrоb{ ≤Х< х₂,}.

Отсюда находим, что искомая вероятность попадания непрерывной случайной величины в интервал х₁≤X<х₂ равна разности функций распределения этой случайной величины:

Рrоb{x1≤Х< х2,} = Рrоb{ ≤Х< х2,} = Рrоb{ ≤Х<x1}≡Fx(x2)-Fx(x1).

Проводя такие же рассуждения, мы можем найти вероятность попадания непрерывной случайной величины в бесконечно малый интервал х≤X < х+dх:

В последних двух равенствах используется определение бесконечно малого изменения функции распределения (или дифференциала этой функции). Из найденного соотношения видно, что вероятность попадания непрерывной случайной величины в бесконечно малый интервал х≤Х<х+dх бесконечна мала и пропорциональна величине этого интервала dх. Отношение этой бесконечно малой вероятности к бесконечно малой величине интервала имеет конечное значение и характеризует плотность вероятности в точке х.

Плотность распределения вероятности:

или наоборот:

На рис. 8 приведен характерный график плотности вероятности, а на рис. 9 - график соответствующей функции распределения.

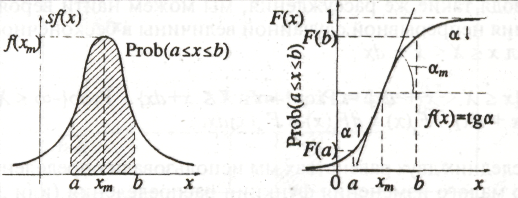
Рис. 8 Рис.9

Наклон графика функции распределения характеризует плотность вероятности (чем больше плотность вероятности, тем быстрее меняется функция распределения) (точнее f(х) = tg(α)), а площадь под графиком функции плотности вероятности на интервале х₁≤X<х₂ характеризует вероятность попадания непрерывной случайной величины в соответствующий интервал.

При этом суммарная площадь под графиком функции плотности вероятности на всем интервале - ≤Х< равна по определению единице:

Равномерное распределение

Если значения случайной величины из некоторого интервала можно считать равновероятными, то мы приходим к равномерному распределению случайной величины. Равномерное распределение - это такое распределение вероятности, плотность которого постоянна в заданном интервале изменения случайной величины X: a≤Х≤b. Равномерно распределенная случайная величина обозначается R(а,b). Там, где встречается R без указания параметров, подразумевается стандартное равномерное распределение на интервале 0≤Х≤1: R(0,1).

Плотность вероятности равномерного распределения на интервале [а, b] постоянна на этом интервале:

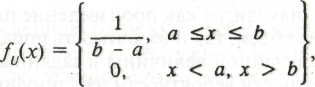
а функция распределения:

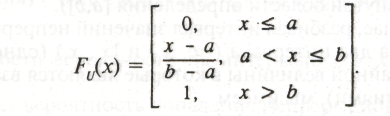
Для равномерного распределения .

Соответствующие этим функциям графики приведены на рисунке 7.

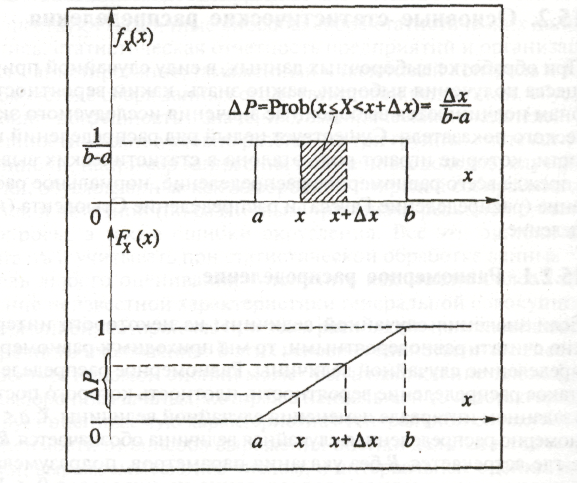
Рис. 7. Плотность распределения и функция распределения равномерного распределения

На примере равномерного распределения проще всего показать как графически и аналитически рассчитывать вероятность попадания в заданный интервал, т.е. Рrоb{х, ≤ Х< х₂}, используя соотношение между плотностью распределения и функцией распределения. Подобно тому, как масса физического тела, равномерно распределенная по объему, находится как произведение плотности (массы в единице объема) на объем, так и вероятность попадания равномерно распределенной случайной величины в заданный интервал равна произведению плотности вероятности на длину интервала, и, таким образом, величина вероятности линейно растет с увеличением длины интервала (внутри области определения [а,b]).