
- •Л.М. Орлова, н.Н. Ивахненко Определенный и несобственный интегралы
- •Содержание
- •Введение
- •1. Определенный интеграл и его свойства
- •1.1. Понятие определенного интеграла
- •1.2. Свойства определенного интеграла. Формула Ньютона–Лейбница
- •1.3. Методы вычисления определенных интегралов
- •1.4. Задания для самостоятельного контроля усвоения
- •2. Приложения определенного интеграла
- •2.1. Площадь плоской фигуры
- •2.2. Длина дуги
- •2.3. Объем тела вращения
- •2.4. Задания для самостоятельного контроля усвоения
- •3. Несобственный интеграл
- •3.1. Несобственные интегралы с бесконечными пределами
- •3.2. Несобственный интеграл от неограниченных функций
- •3.3.3. Задания для самостоятельного контроля усвоения
- •4. Комплексные тестовые задания для индивидуального решения
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •5. Ответы к заданиям для самостоятельного контроля усвоения материала
- •5.1. Ответы к заданиям для самостоятельного контроля
- •5.2. Ответы к заданиям для самостоятельного контроля
- •5.3. Ответы к заданиям для самостоятельного контроля
- •3.3.3. Задания для самостоятельного контроля усвоения
- •4. Комплексные тестовые задания для индивидуального решения
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •5. Ответы к заданиям для самостоятельного контроля усвоения материала
- •5.1. Ответы к заданиям для самостоятельного контроля
- •5.2. Ответы к заданиям для самостоятельного контроля
- •5.3. Ответы к заданиям для самостоятельного контроля
- •3.3.3. Задания для самостоятельного контроля усвоения
- •4. Комплексные тестовые задания для индивидуального решения
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •5. Ответы к заданиям для самостоятельного контроля усвоения материала
- •5.1. Ответы к заданиям для самостоятельного контроля
- •5.2. Ответы к заданиям для самостоятельного контроля
- •5.3. Ответы к заданиям для самостоятельного контроля
- •Литература
- •Предметный указатель
1.4. Задания для самостоятельного контроля усвоения
материала к разделу 1
Вычислить определенные интегралы:
1.4.1. EMBED Equation.3
 .
1.4.2. EMBED Equation.3
.
1.4.2. EMBED Equation.3
 1.4.3.
EMBED Equation.3
1.4.3.
EMBED Equation.3
 .
1.4.4. EMBED
Equation.3
.
1.4.4. EMBED
Equation.3
 .
1.4.5. EMBED
Equation.3
.
1.4.5. EMBED
Equation.3
 .
1.4.6. EMBED
Equation.3
.
1.4.6. EMBED
Equation.3
 .
1.4.7. EMBED
Equation.3
.
1.4.7. EMBED
Equation.3
 .
1.4.8. EMBED
Equation.3
.
1.4.8. EMBED
Equation.3
 .
1.4.9. EMBED
Equation.3
.
1.4.9. EMBED
Equation.3
 .
1.4.10. EMBED
Equation.3
.
1.4.10. EMBED
Equation.3
 .
1.4.11. EMBED
Equation.3
.
1.4.11. EMBED
Equation.3
 .
1.4.12. EMBED
Equation.3
.
1.4.12. EMBED
Equation.3
 .
1.4.13. EMBED
Equation.3
.
1.4.13. EMBED
Equation.3
 .
1.4.14. EMBED
Equation.3
.
1.4.14. EMBED
Equation.3
 .
1.4.15. EMBED
Equation.3
.
1.4.15. EMBED
Equation.3
 .
1.4.16. EMBED
Equation.3
.
1.4.16. EMBED
Equation.3
 .
1.4.17. EMBED
Equation.3
.
1.4.17. EMBED
Equation.3
 .
1.4.18. EMBED
Equation.3
.
1.4.18. EMBED
Equation.3
 .
1.4.19. EMBED
Equation.3
.
1.4.19. EMBED
Equation.3
 .
1.4.20. EMBED
Equation.3
.
1.4.20. EMBED
Equation.3
 .
1.4.21. EMBED
Equation.3
.
1.4.21. EMBED
Equation.3
 .
1.4.22. EMBED
Equation.3
.
1.4.22. EMBED
Equation.3
 .
1.4.23. EMBED
Equation.3
.
1.4.23. EMBED
Equation.3
 .
1.4.24. EMBED
Equation.3
.
1.4.24. EMBED
Equation.3
 .
1.4.25. EMBED
Equation.3
.
1.4.25. EMBED
Equation.3
 .
1.4.26. EMBED
Equation.3
.
1.4.26. EMBED
Equation.3
 .
1.4.27. EMBED
Equation.3
.
1.4.27. EMBED
Equation.3
 .
1.4.28. EMBED
Equation.3
.
1.4.28. EMBED
Equation.3
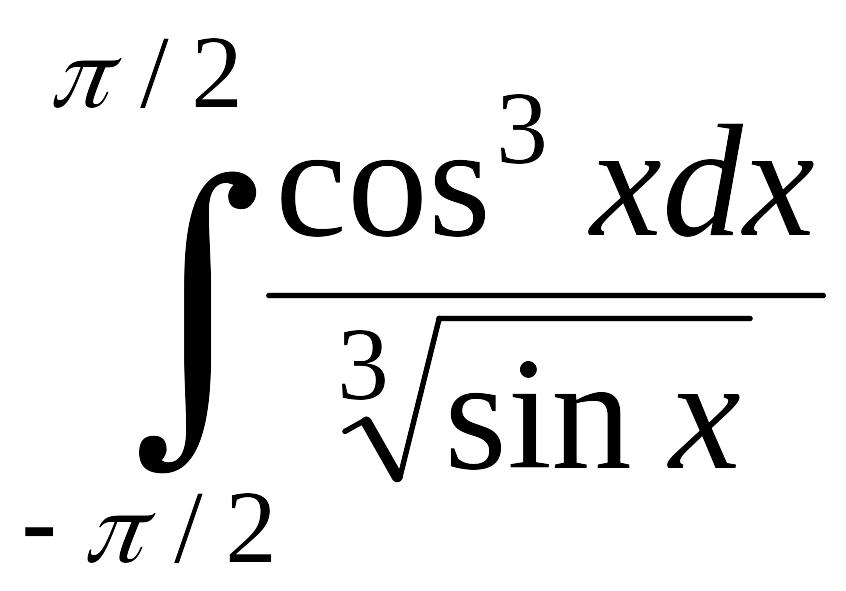 .
1.4.29. EMBED
Equation.3
.
1.4.29. EMBED
Equation.3
 .
1.4.30. EMBED
Equation.3
.
1.4.30. EMBED
Equation.3
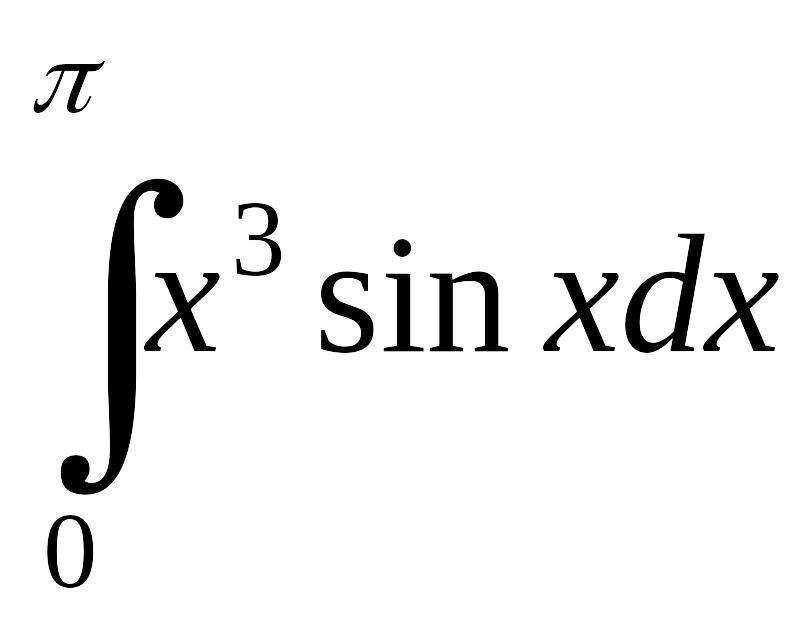 .
1.4.31. EMBED
Equation.3
.
1.4.31. EMBED
Equation.3
 .
1.4.32. EMBED
Equation.3
.
1.4.32. EMBED
Equation.3
 .
1.4.33. EMBED
Equation.3
.
1.4.33. EMBED
Equation.3
 .
1.4.34. EMBED
Equation.3
.
1.4.34. EMBED
Equation.3
 .
1.4.35. EMBED
Equation.3
.
1.4.35. EMBED
Equation.3
 .
1.4.36. EMBED
Equation.3
.
1.4.36. EMBED
Equation.3
 .
1.4.37. EMBED
Equation.3
.
1.4.37. EMBED
Equation.3
 .
1.4.38. EMBED
Equation.3
.
1.4.38. EMBED
Equation.3
 .
1.4.39. EMBED
Equation.3
.
1.4.39. EMBED
Equation.3
 .
1.4.40. EMBED
Equation.3
.
1.4.40. EMBED
Equation.3
 .
1.4.41. EMBED
Equation.3
.
1.4.41. EMBED
Equation.3
 .
1.4.42. EMBED
Equation.3
.
1.4.42. EMBED
Equation.3
 .
1.4.43. EMBED
Equation.3
.
1.4.43. EMBED
Equation.3
 .
1.4.44. EMBED
Equation.3
.
1.4.44. EMBED
Equation.3
 .
1.4.45. EMBED
Equation.3
.
1.4.45. EMBED
Equation.3
 .
1.4.46. EMBED
Equation.3
.
1.4.46. EMBED
Equation.3
 .
1.4.47. EMBED
Equation.3
.
1.4.47. EMBED
Equation.3
 .
1.4.48. EMBED
Equation.3
.
1.4.48. EMBED
Equation.3
 .
1.4.49. EMBED
Equation.3
.
1.4.49. EMBED
Equation.3
 .
1.4.50. EMBED
Equation.3
.
1.4.50. EMBED
Equation.3
 .
1.4.51. EMBED
Equation.3
.
1.4.51. EMBED
Equation.3
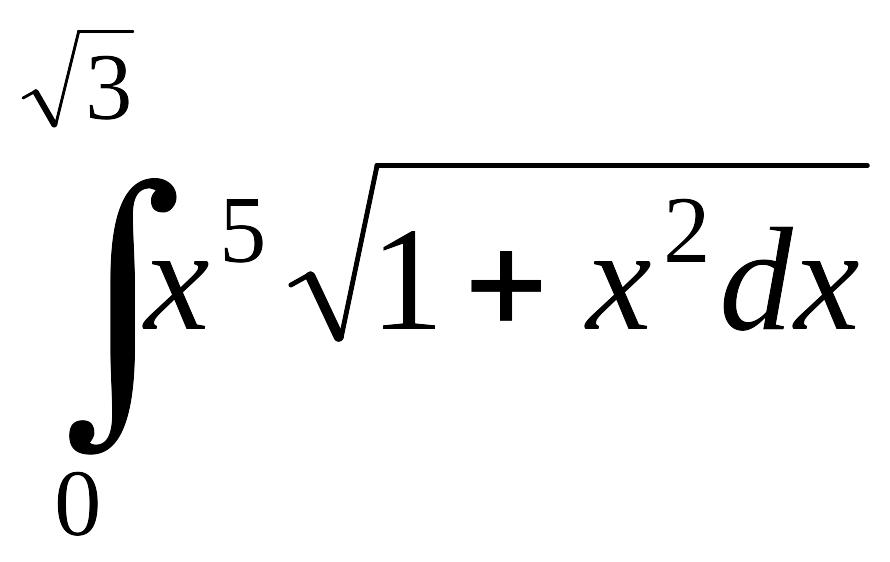 .
1.4.52. EMBED
Equation.3
.
1.4.52. EMBED
Equation.3
 .
1.4.53. EMBED
Equation.3
.
1.4.53. EMBED
Equation.3
 .
1.4.54. EMBED
Equation.3
.
1.4.54. EMBED
Equation.3
 .
1.4.55. EMBED
Equation.3
.
1.4.55. EMBED
Equation.3
 .
1.4.56. EMBED
Equation.3
.
1.4.56. EMBED
Equation.3
 .
1.4.57. EMBED
Equation.3
.
1.4.57. EMBED
Equation.3
 .
1.4.58. EMBED
Equation.3
.
1.4.58. EMBED
Equation.3
 .
1.4.59. EMBED
Equation.3
.
1.4.59. EMBED
Equation.3
 .
1.4.60. EMBED
Equation.3
.
1.4.60. EMBED
Equation.3
 .
1.4.61. EMBED
Equation.3
.
1.4.61. EMBED
Equation.3
 .
1.4.62. EMBED
Equation.3
.
1.4.62. EMBED
Equation.3
 .
1.4.63. EMBED
Equation.3
.
1.4.63. EMBED
Equation.3
 .
1.4.64. EMBED
Equation.3
.
1.4.64. EMBED
Equation.3
 .
1.4.65. EMBED
Equation.3
.
1.4.65. EMBED
Equation.3
 .
1.4.66. EMBED
Equation.3
.
1.4.66. EMBED
Equation.3
 .
1.4.67. EMBED
Equation.3
.
1.4.67. EMBED
Equation.3
 .
1.4.68. EMBED
Equation.3
.
1.4.68. EMBED
Equation.3
 .
1.4.69. EMBED
Equation.3
.
1.4.69. EMBED
Equation.3
 .
1.4.70. EMBED
Equation.3
.
1.4.70. EMBED
Equation.3
 .
1.4.71. EMBED
Equation.3
.
1.4.71. EMBED
Equation.3
 .
1.4.72. EMBED
Equation.3
.
1.4.72. EMBED
Equation.3
 .
1.4.73. EMBED
Equation.3
.
1.4.73. EMBED
Equation.3
 .
1.4.74. EMBED
Equation.3
.
1.4.74. EMBED
Equation.3
 .
1.4.75. EMBED
Equation.3
.
1.4.75. EMBED
Equation.3
 .
1.4.76. EMBED
Equation.3
.
1.4.76. EMBED
Equation.3
 .
1.4.77. EMBED
Equation.3
.
1.4.77. EMBED
Equation.3
 .
1.4.78. EMBED
Equation.3
.
1.4.78. EMBED
Equation.3
 .
1.4.79. EMBED
Equation.3
.
1.4.79. EMBED
Equation.3
 .
1.4.80. EMBED
Equation.3
.
1.4.80. EMBED
Equation.3
 .
1.4.81. EMBED
Equation.3
.
1.4.81. EMBED
Equation.3
 .
1.4.82. EMBED
Equation.3
.
1.4.82. EMBED
Equation.3
 .
1.4.83. EMBED
Equation.3
.
1.4.83. EMBED
Equation.3
 .
1.4.84. EMBED
Equation.3
.
1.4.84. EMBED
Equation.3
 .
.
1.4.85.
EMBED Equation.3
 .
1.4.86. EMBED
Equation.3
.
1.4.86. EMBED
Equation.3
 .
.
2. Приложения определенного интеграла
2.1. Площадь плоской фигуры
Из геометрического смысла определенного интеграла известно, что площадь криволинейной трапеции, ограниченной непрерывной кривой у = f(x) (функция у = f(x) неотрицательна), прямыми x = a, x = b и отрезком оси абсцисс a x b, вычисляется по формуле (1.1.2), т.е.
EMBED Equation.3
 .
(1.1.2)
.
(1.1.2)
Площадь фигуры (рис.2.1.1), ограниченной двумя непрерывными кривыми y = f1(x) и y = f2(x) (f1(x) f2(x)), прямыми x = a, x = b и отрезком оси абсцисс a x b, вычисляется по формуле (2.1.1)
EMBED Equation.3
 .
(2.1.1)
.
(2.1.1)
SHAPE \* MERGEFORMAT
 SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT
Рисунок 2.1.1 - Плоская фигура
Если функция y = f(x) непрерывная и неположительная на отрезке [a, b] (рис 2.1.2), то определенный интеграл от функции y = f(x) в пределах интегрирования от а до b является отрицательным, т.е.
EMBED Equation.3
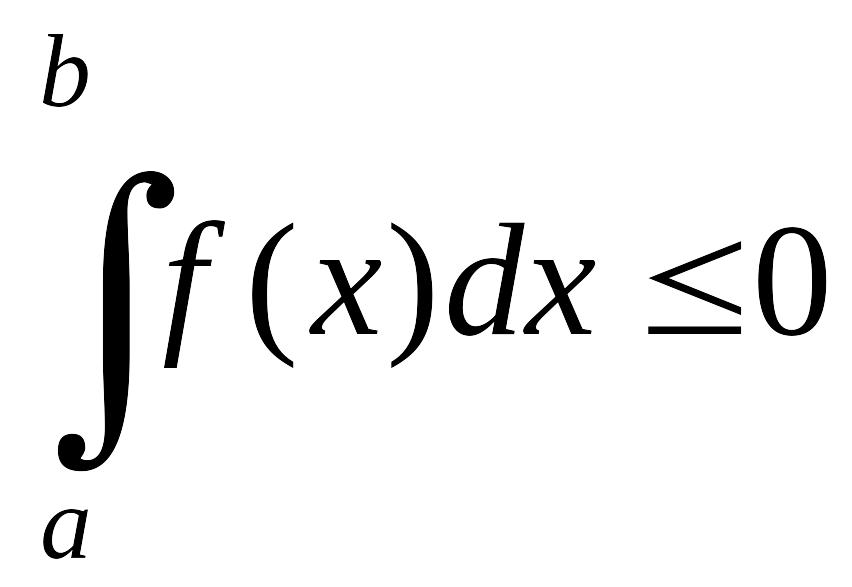 .
(2.1.2)
.
(2.1.2)
у
b
a
0
x
y = f(x)
Рисунок 2.1.2 - Криволинейная трапеция
А
y
a
0
EMBED Equation.3
 .
(2.1.3)
.
(2.1.3)
Если функция y
= f(x)
непрерывная и не знакопостоянная на
отрезке [a,
b], то
определенный интеграл EMBED Equation.3
 численно равен
алгебраической сумме площадей
криволинейных трапеций, лежащих над и
под осью Оx
(рис. 2.1.2).
численно равен
алгебраической сумме площадей
криволинейных трапеций, лежащих над и
под осью Оx
(рис. 2.1.2).
y
y
x
y=f(x)
d
а
c
0
b

Рисунок 2.1.3 - Плоская фигура
Т
a
с
d
0
EMBED Equation.3
 EMBED Equation.3
EMBED Equation.3
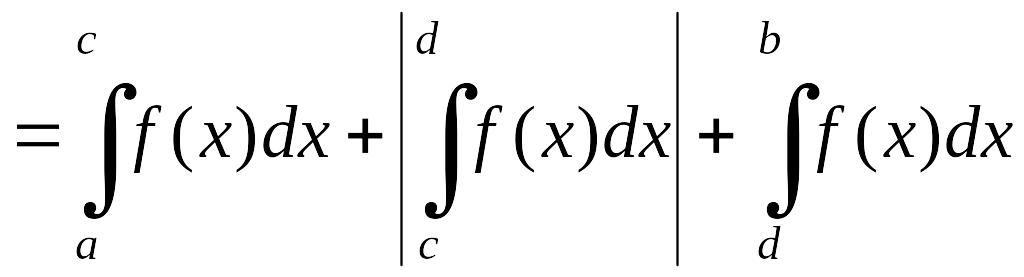 . (2.1.3)
. (2.1.3)
В случае
параметрического задания кривой EMBED
Equation.3
![]() площадь криволинейной трапеции,
ограниченной этой кривой, двумя прямыми
EMBED Equation.3
площадь криволинейной трапеции,
ограниченной этой кривой, двумя прямыми
EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() и отрезком оси Ох
EMBED Equation.3
и отрезком оси Ох
EMBED Equation.3
![]() ,
можно найти по формуле
,
можно найти по формуле
EMBED Equation.3
 (2.1.4.)
(2.1.4.)
где пределы
интегрирования EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() определяются из уравнений EMBED Equation.3
определяются из уравнений EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() ,
при этом EMBED Equation.3
,
при этом EMBED Equation.3
![]() на отрезке EMBED Equation.3
на отрезке EMBED Equation.3
![]() .
.
Пример 2.1.1. Найти площадь плоской фигуры, ограниченной следующими линиями у = x, y = x2, х = 2.
Решение. Изобразим на рис. 2.1.4 плоскую фигуру, площадь которой нужно найти.
SHAPE \* MERGEFORMAT

Рисунок 2.1.4 - Плоская фигура
Для того, чтобы
определить пределы о
0
EMBED Equation.3

Таким образом, точки с координатами (0, 0) и (1, 1) являются точками пересечения данных прямой у = x и параболы y = x2. Значит нижний предел интегрирования равен а = 1.
Поскольку рассматриваемая плоская фигура ограничена справа прямой х = 2, то верхний предел интегрирования равен b =2.
Таким образом, по формуле (2.1.1)
EMBED Equation.3
 (ед.кв.)
(ед.кв.)
Пример 2.1.2
Найти площадь фигуры, ограниченной
первой аркой циклоиды EMBED Equation.3
![]() и отрезком оси абсцисс.
и отрезком оси абсцисс.
Решение.
Изобразим на рис. 2.1.5 циклоиду, площадь
первой арки которой нужно найти. Точкам
О
и А соответствуют
значения параметра EMBED Equation.3
![]() и EMBED Equation.3
и EMBED Equation.3
![]() .
.
 SHAPE
\* MERGEFORMAT
SHAPE
\* MERGEFORMAT

Рисунок 2.1.5 - Циклоида
поэтому по формуле (2.1.4.) искомая площадь
EMBED Equation.3
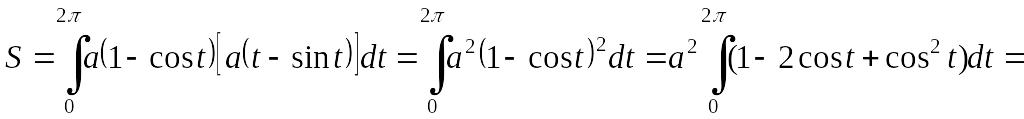
EMBED Equation.3
 (ед.кв.)
(ед.кв.)
