
- •Розділ 8. Диференціальні рівняння
- •1. Економічні задачі, що приводять до диференціальних рівнянь. Основні означення
- •2. Диференціальні рівняння першого порядку
- •Диференціальні рівняння першого порядку з подільними змінними.
- •Однорідні диференціальні рівняння першого порядку.
- •Лінійні диференціальні рівняння першого порядку.
- •Рівняння Бернуллі.
- •Рівняння в повних диференціалах.
- •3. Диференціальні рівняння другого порядку
- •Деякі диференціальні рівняння другого порядку, що допускають зниження порядку.
- •Лінійні однорідні диференціальні рівняння другого порядку. Загальні властивості.
- •4. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами
- •5. Лінійні неоднорідні диференціальні рівняння другого порядку. Метод варіації довільних сталих
- •6. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами
- •7. Системи диференціальних рівнянь
- •Системи лінійних однорідних диференціальних рівнянь зі сталими коефіцієнтами.
- •8. Задачі економічної динаміки
- •Відповіді до вправ Розділ 1
- •Розділ 2
- •Розділ 3
- •Розділ 4
- •Розділ 5
- •Розділ 6
- •Розділ 7
- •Розділ 8
- •Список літератури
- •Математичний аналіз для економістів
Деякі диференціальні рівняння другого порядку, що допускають зниження порядку.
1. Найпростіше диференціальне рівняння другого порядку має вигляд
![]() .
(8.18)
.
(8.18)
Послідовно двічі інтегруючи і тим самим знижуючи порядок рівняння, будемо мати
![]() ,
,
![]() ,
,
Приклад
8.7. Знайти
частинний розв'язок диференціального
рівняння
![]() ,
що задовольняє початковим умовам
,
що задовольняє початковим умовам
![]() ,
,
![]() .
.
Розв’язання. Загальний розв'язок диференціального рівняння одержуємо, двічі інтегруючи його послідовно:
![]() ,
,
![]() .
.
Підставляючи у
вирази початкові умови, одержуємо
систему рівнянь для визначення значень
![]() і
і
![]() :
:
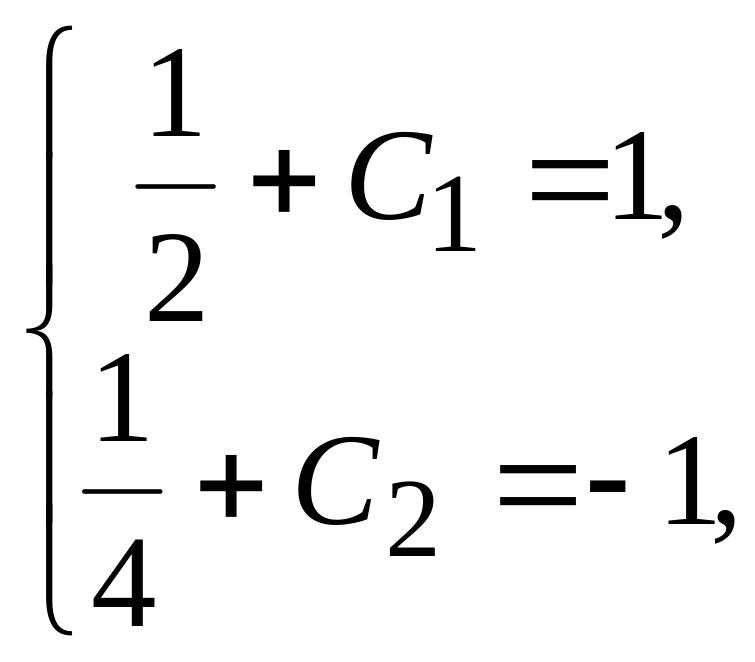 звідки
звідки

Шуканий частинний
розв'язок має вигляд
![]() .
.
2. Диференціальне рівняння другого порядку, що не містить явно функції , має вигляд
![]() .
(8.19)
.
(8.19)
Введемо нову
невідому функцію, прийнявши
![]() ,
,
![]() .
Тоді рівняння (8.19) буде
.
Тоді рівняння (8.19) буде
![]() .
.
Це диференціальне
рівняння першого порядку відносно
функції
![]() .
Розв’язуючи його, одержуємо
.
Розв’язуючи його, одержуємо
![]() .
.
Підставляючи замість його значення , приходимо до найпростішого диференціального рівняння першого порядку
![]() .
.
Проінтегрувавши його, одержимо загальний розв'язок даного рівняння
![]() .
.
Приклад
8.8. Знайти
частинний розв'язок диференціального
рівняння
![]() ,
що задовольняє початковим умовам
,
що задовольняє початковим умовам
![]() ,
,
![]() .
.
Розв’язання.
Дане рівняння не містить явно шуканої
функції, тому замінимо
,
,
одержимо диференціальне рівняння
![]() ,
що є лінійним рівнянням першого порядку.
,
що є лінійним рівнянням першого порядку.
Знайдемо допоміжну
функцію
у вигляді
![]() .
Тоді
.
Тоді
![]() .
Підставимо значення
і
.
Підставимо значення
і
![]() в рівняння і підберемо функції
і
так, щоб виконувалася рівність
в рівняння і підберемо функції
і
так, щоб виконувалася рівність
![]() або
або
![]() .
.
Складемо систему рівнянь для визначення функцій і :

Розв’язуючи перше
рівняння, знаходимо, що
![]() .
Підставивши знайдене значення
у друге рівняння і розв’язавши його
відносно функції
,
одержимо
.
Підставивши знайдене значення
у друге рівняння і розв’язавши його
відносно функції
,
одержимо
![]() .
.
Отже,
![]() або
або
![]() .
Але оскільки
.
Але оскільки
![]() ,
то загальний розв'язок заданого рівняння
знайдемо, проінтегрувавши функцію
,
то загальний розв'язок заданого рівняння
знайдемо, проінтегрувавши функцію
![]() .
.
Інтегруючи, маємо
![]() .
.
Щоб із загального
розв'язку рівняння виділити частинний,
який задовольняє початковим умовам
,
,
підставимо значення
![]() ,
,
![]() ,
,
![]() ,
одержимо, що
,
одержимо, що
![]() ,
,
![]() .
.
Отже, частинний розв'язок даного рівняння має вигляд
![]() .
.
3. Диференціальне рівняння другого порядку, що не містить явно незалежної змінної має вигляд
![]() .
(8.20)
.
(8.20)
Таке рівняння
допускає зниження порядку, якщо за нову
незалежну змінну взяти
,
а за нову шукану функцію взяти
![]() .
.
Тоді, застосувавши
правило диференціювання складної
функції, одержимо
![]() або
або
![]() .
.
Підставляючи значення й у рівняння (8.20) одержуємо диференціальне рівняння першого порядку відносно функції
![]() .
.
Розв'язок цього
рівняння знайдемо у вигляді
![]() .
.
Замінюючи
![]() ,
одержуємо
,
одержуємо
![]() – рівняння з подільними змінними. Після
поділу змінних прийдемо до рівності
– рівняння з подільними змінними. Після
поділу змінних прийдемо до рівності
![]() ,
інтегруючи яку, знайдемо загальний
розв'язок даного рівняння у вигляді
,
інтегруючи яку, знайдемо загальний
розв'язок даного рівняння у вигляді
![]() .
.
Приклад
8.9. Знайти
загальний розв'язок диференціального
рівняння
![]() .
.
Розв’язання.
Дане рівняння не містить у собі явно
незалежну змінну
.
Замінимо
![]() ,
.
Одержимо рівняння
,
.
Одержимо рівняння
![]() ,
яке є рівнянням з подільними змінними.
Після поділу змінних прийдемо до рівняння
,
яке є рівнянням з подільними змінними.
Після поділу змінних прийдемо до рівняння
![]() ,
інтегруючи яке маємо
,
інтегруючи яке маємо
![]() або
або
![]() .
Звідки
.
Звідки
![]() .
.
Оскільки
,
то розв’яжемо рівняння
![]() або
або
![]() .
Інтегруючи, одержуємо
.
Інтегруючи, одержуємо
![]() – загальний інтеграл заданого рівняння
– загальний інтеграл заданого рівняння
