Логика первого порядка неразрешима

В этой главе мы докажем, что не существует механически вычислимой процедуры, которая позволяет определять общезначимость произвольного предложения логики предикатов первого порядка. Иными словами мы докажем, что логика предикатов первого порядка неразрешима.

Говорят, что проблема распознавания какого-либо свойства разрешима, если существует допускающий механическое вычисление тест (вычислимая, или эффективная процедура), которая будучи применена к произвольному объекту соответствующего типа, после некоторого конечного числа шагов правильно классифицирует этот объект с точки зрения наличия или отсутствия у него этого свойства.

Позитивным тестомназывается эффективная процедура, устанавливающая за конечное число шагов все случаи наличия соответствующего свойства и только их. Если объект обладает соответствующим свойством, позитивный тест обязан сказать "Да". Если объект не обладает соответствующим свойством, позитивный тест вовсе не обязан сказать "Нет", а может работать бесконечно долго.

Негативным тестомназывается эффективная процедура, устанавливающая за конечное число шагов все случаи отсутствия соответствующего свойства и только их.

Проблема распознавания произвольного свойства разрешима тогда и только тогда, когда для него существует и позитивный, и негативный тесты. Всякий объект может обладать рассматриваемым свойством, или нет. Если мы одновременно запустим и позитивный, и негативный тесты, то через конечное число шагов один из них правильно классифицирует наш объект.

Мы будем сейчас рассматривать свойства общезначимости и выполнимости. А в качестве объектов будут выступать преложения логики предикатов первого порядка.

Пусть запись ÞSбудет обозначать, что предложениеS общезначимо.

Докажем, что S₁ÞS₂ тогда и только тогда, когда Þ(S₁®S₂).

Доказательство. Предложение (S₁®S₂) в соответствии с пунктом 4 определения понятия интерпретации будет истинно в интерпретацииc, если всякий раз, когдаc( S₁)=1 будет верно равенствоc( S₂)=1. Если это будет верно для любой интепретации, которая одновременно интерпретируетS₁ иS₂, то предложение (S₁®S₂) будет общезначимым. Но по нашему определению логическое следованиеS₁ÞS₂имеет место, когда из того, чтоc( S₁)=1 следует, чтоc( S₂)=1 для любой интерпретации c. То есть, общезначимость предложения (S₁®S₂) и логическое следованиеS₁ÞS₂означают одно и то же.

Это утверждение можно обобщить.

S₁ ,...,S_nÞS_n+1 тогда и только тогда, когда Þ( S₁ Ù...ÙS_n ® S_n+1)

Доказательство. Условие S₁ ,...,S_nÞS_n+1нарушается в точности тогда, когда существует интерпретацияc, при которойc(S₁)=...=c(S_n)=1 и c(S_n+1)=0. Но второе условиеÞ( S₁ Ù...ÙS_n ® S_n+1) нарушается точно тогда же.

Докажем неразрешимость логики предикатов первого порядка от противного: мы докажем, что если бы существовал тест для распознавания общезначимости или выполнимости, то проблема остановки машин Тьюринга оказалась бы разрешимой. Но мы уже доказали, что, если только тезис Черча верен, проблема остановки неразрешима.

Наше доказательство будет строиться так: мы покажем, как по описанию машины Тьюринга и натуральному числу nможно эффективно построить такое конечное множество предложенийDи еще одно предложениеH, что DÞHтогда и только тогда, когда рассматриваемая машина, будучи запущена сn единицами на входе, останавливается через некоторое время. Для каждой машины и числа единиц на входе мы, таким образом, определяем некоторую интерпретациюc.

Предложение Hв интерпретацииcговорит, что машина в конце концов остановится, а предложения из множестваDописывают работу машины, ее начальную конфигурацию, а также сообщают кое-что о функции следованияs. Таким образом, если бы проблема распознавания общезначимости предложений была разрешима, мы смогли бы эффективно решать проблему остановки, поскольку логическое следованиеDHимеет место тогда и только тогда, когда общезначимо некоторое предложение, а именно импликация, в левой части которой стоит конъюнкция всех предложений множестваD, а справа предложениеH.

Будем читать, что клетки ленты машины занумерованы так:

... -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 ...

Будем также предполагать, что время разбито на бесконечную последовательность моментов t, в каждый из которых машина выполняет точно одну операцию. Машина начинает работу в момент времени 0 и считывает при этом клетку с номером 0. Мы считаем, что машина "включается" в момент времени 0 и "выключается" в первый момент, который следует за моментом остановки. Мы считаем далее, что во все отрицательные моменты времени и во все моменты, следующие за моментом остановки машины, она не находится ни в каком состоянии, не считывает никакую из имеющихся клеток и никакой символ (даже пустой) не встречается нигде на ее ленте.

Область интерпретации cмножества предложенийDÈ{H} совпадает с множеством целых чисел. ИмениOинтерпретация приписывает значение ноль, а функциональному символуsфункцию следования. Предикатные символыQ_i,S_j,LT,EQинтерпретируются следующим образом:

Q_i(t,x) истинно тогда и только тогда, когда машина в момент времениtнаходится в состоянииq_i, считывая при этом клетку с номеромx;

S_j(t,x) истинно тогда и только тогда, когда в клетке номеромxнаходится символS_j;

LT(x,y)истинно тогда и только тогда, когда xменьшеy;

EQ(x,y)истинно тогда и только тогда, когда x равноy.

Для упрощения будем считать, что алфавит машины состоит из символов S₀иS₁. Хотя наше доказательство на самом деле не будет зависеть от размера алфавита нашей машины.

Для каждого фрагмента граф-схемы машины, имеющего вид

S_j:S_k

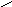im

мы включим в множество D предложение

("t)("x)("y)[Q_i(t,x)ÙS_j(t,x)®(Q_m(s(t),x)ÙS_k(s(t),x)Ù

__{__}

Ù(EQ(y,x)®((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))](1)

В нашей интерпретации это предложение звучит так: Если в момент времени tмашина находится в состоянииq_i, считывая при этом символS_jв клеткеx, то в моментt+1 машина перейдет в состояниеq_m, считывая при этом клеткуx, в которой появится символ S_k, а во всех клетках, отличных отx, в момент t+1 останутся те же символы, что в моментt. При этом не исключается совпадениеi=m. Этот случай соответствует петле в графе переходов. Аналогично рассматриваются и следующие два типа переходов в графе переходов.

Для каждого фрагмента граф-схемы машины, имеющего вид

S_j:R

im

мы включим в множество Dпредложение

("t)("x)("y)[Q_i(t,x)ÙS_j(t,x)®(Q_m(s(t),s(x))Ù

Ù((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))](2)

Для каждого фрагмента граф-схемы машины, имеющего вид

S_j:L

im

мы включим в множество Dпредложение

("t)("x)("y)[Q_i(t,s(x))ÙS_j(t,s(x))®(Q_m(s(t),x)Ù

Ù((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))](3)

Одно из предложений множества Dутверждает, что в начальный момент машина находится в состоянииq₁, считывая при этом клетку с номером 0 и самую левую единицу в сплошном массиве изnединиц на ленте с нулями в остальных клетках:

Q₁(O,O)ÙS₁(O,O)ÙS₁(O,s(O))Ù...ÙS₁(O, O^(n-1))Ù

_{____ ____ ____}

Ù("y)(EQ(y,O)ÙEQ(y,s(O))Ù...ÙEQ(y, O^(n-1)))®S₀(O,y)) (4)

Здесь O^(n-1)означает применениеn-1 раз символов функции следованияsк символуO.

Еще одно из предложений множества D утверждает, что всякое целое число является следующим точно за одним целым:

("z)($x)EQ(z,s(x))Ù("z)("x)(")[EQ(z,s(x))ÙEQ(z,s(y))®EQ(x,y)](5)

Если pиq различные натуральные числа, то предложение

__{__}

("x)EQ(x^(p),x^(q))должно следовать изD. Все такие предложения являются следствиям предложения

("x)("y)("z)(LT(x,y)ЩLT(y,z)®LT(x,z))Щ("x)("y)(EQ(s(x),y)®LT(x,y)Щ

___{_}

Щ("x)("y)(LT(x,y)®EQ(x,y)) (6)

Включим в множество D все предложения (1),(2),(3), соответствующие всем стрелкам графа переходов данной машины, вместе стремя дополнительными предложениями (4),(5),(6). Понятно, чтоcслужит моделью дляD.

За предложение Hпримем дизъюнкцию всех предложений вида($t)($x)[Q_i(t,x)ÙS_j(t,x)](7),

для которых в машинной таблице нет команд, соответствующим комбинациям q_i, S_j. Если же для всякой такой комбинации в таблице имеются команды, то машина никогда не остановится, и заHв этом случае принимаем любое предложение, ложное в интерпретацииc,

_{____}

например EQ(O,O).

Итак мы показали, как по данной машине и входному значению nпостроить такое конечное множество предложенийD и еще одно отдельноеH, что (мы должны доказать это) соотношениеDÞHимеет место тогда и только тогда, когда машина, получив n на входе в конце концов останавливается.

Часть “только тогда” доказывается просто. Все предложения множества D истинны в нашей интерпретацииc. Поэтому, если изD следуетH, тоc(H)=1. НоHистинно вcтогда и только тогда, когда машина останавливается, получивnна входе.

Часть “тогда” доказывается труднее.

Введем некоторые обозначения. Пусть p- отрицательное целое число иp=-q.Тогда формулу($z)[Q_i(t,z)ÙEQ(z^(q),O)] будем сокращенно записывать в видеQ_i(t,O^(p)). Формулу($z)[S_j(t,z)ÙEQ(z^(q),O)] обозначим какS_j(t,O^(p)). И формулу

_{_____ _____}

($z)[ EQ(y,z)ÙEQ(z^(q),O)] обозначим какEQ(t,O^(p)).

Введем теперь специальный тип предложений, называемых описаниями времениt. Так называется всякое предложение, определяющее в каком состоянии находится машина в момент времениt, какая клетка при этом считывается и какие символы записаны в клетках ленты. Описание времениtесть предложение вида

Q_i(O^(t), O^(p))ÙS_j1(O^(t),O^(p1))Ù... ÙS_j(O^(t),O^(p))Ù... ÙS_jv(O^(t),O^(pv)) Ù

_{____ ____ ____}

Ù("y)[EQ(y,O^(p1))Ù...ÙEQ(y,O^(p))Ù... ÙEQ(y,O^(pv))® S₀(O^(t),y)](8)

При этом последовательность целых чисел p1,...,p,...,pv -возрастающая. Числоpможет совпадать сp1 или сpv. По этому определению предложение (4) есть описание времени 0.

Предположим, что машина остановится в некоторый момент времени t. Тогда для некоторыхt,i,pи jмашина в момент времениtокажется в состоянииq_i, будет считывать клетку с номером p, в которой будет находится символS_j. Причем в машинной таблице нет инструкции для комбинацииq_i, S_j.

Предположим, далее, что из множества D следует некоторое описаниеGвремениt. Посколькуc модель дляD, тоc(G)=1. ПоэтомуGдолжно содержать в качестве конъюнктивных членов предложенияQ_i(O^(t), O^(p)) иS_j(O^(t),O^(p)). Поэтому изGбудет следовать предложение($t)($x)[Q_i(t,x)ÙS_j(t,x)]. Последнее предложение входит одним из дизъюнктивных членов вH. Поэтому изDбудет следоватьH.

Теперь нам осталось показать, что для любого неотрицательного t, если только машина не останавливается до момента t, из D следует описание времени t.

Докажем это индукцией по t. При t=0 множествоD содержит предложение (4), которое является описанием времени 0. Следовательно при t=0DÞG.

Предположим, что доказываемое предложение верно для t и машина не остановилась до момента t+1. Докажем теперь, что изD следует описание времениt+1. Посколькуcмодель дляD, предложение (8) истинно вc. Поэтому машина в момент времениtнаходится в состоянииq_i, считывать клетку с номером p, в которой находится символS_j. Поскольку машина в моментtеще не остановилась, в ее графе переходов должна присутствовать дуга одного из трех типов.

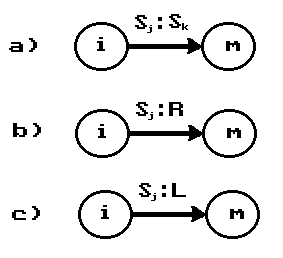
Если имеется стрелка типа а), то в множестве Dприсутствует предложение

("t)("x)("y)[Q_i(t,x)ÙS_j(t,x)®(Q_m(s(t),x)ÙS_k(s(t),x)Ù

__{__}

Ù(EQ(y,x)®((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))]

Из этого предложения и предложений (5), (6) и (8) следует предложение

Q_m(O^(t+1), O^(p))ÙS_j1(O^(t+1),O^(p1))Ù... ÙS_k(O^(t+1),O^(p))Ù... ÙS_jv(O^(t+1),O^(pv)) Ù

_{____ ____ ____}

Ù("y)[EQ(y,O^(p1))Ù...ÙEQ(y,O^(p))Ù... ÙEQ(y,O^(pv))® S₀(O^(t+1),y)]

которое является описанием времени t+1.

Если имеется стрелка типа b), то в множестве Dприсутствует предложение

("t)("x)("y)[Q_i(t,x)ÙS_j(t,x)®(Q_m(s(t),s(x))Ù

Ù((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))]

Из этого предложения и предложений (5), (6) и (8) следует предложение

Q_m(O^(t+1), O^(p+1))ÙS_j1(O^(t+1),O^(p1))Ù... ÙS_j(O^(t+1),O^(p))ÙS_q(O^(t+1),O^(p+1))Ù... ÙS_jv(O^(t+1),O^(pv)) Ù

_{____ ____ ____ ____}

Ù("y)[EQ(y,O^(p1))Ù...ÙEQ(y,O^(p))ÙEQ(y,O^(p+1))Ù... ÙEQ(y,O^(pv))® S₀(O^(t+1),y)]

где S_q - некоторый символ. Это предложение является описанием времениt+1.

Если имеется стрелка типа с), то в множестве Dприсутствует предложение

("t)("x)("y)[Q_i(t,x)ÙS_j(t,x)®(Q_m(s(t),x)ÙS_k(s(t),x)Ù

__{__}

Ù(EQ(y,x)®((S₀(t,y)®S₀(s(t),y))Ù(S₁(t,y)®S₁(s(t),y)))]

Тогда существует такой символ S_q, что из последнего предложения и предложений (5), (6) и (8) следует предложение

Q_m(O^(t+1), O^(p-1))ÙS_j1(O^(t+1),O^(p1))Ù...ÙS_q(O^(t+1),O^(p-1))ÙS_j(O^(t+1),O^(p)) Ù... ÙS_jv(O^(t+1),O^(pv)) Ù

_{____ ____ ____ ____}

Ù("y)[EQ(y,O^(p1))Ù...ÙEQ(y,O^(p-1))EQ(y,O^(p)) Ù... ÙEQ(y,O^(pv))® S₀(O^(t+1),y)]

А это предложение является описанием времени t+1.

Во всех трех случаях множество Dимеет следствием описание времениt+1, и мы доказали неразрешимость логики первого порядка.