Функции, вычислимые на машине Тьюринга
Определим теперь понятие вычислимости по Тьюрингу. Мы ограничимся пока машинами с алфавитом {1,0} и функциями одной переменной из натуральных чисел в натуральные . Чтобы вычислить значение некоторой функцииfв точкеn (если функция определена в этой точке) машинаM начинает работу в состоянии с наименьшим номером встандартной конфигурации сnединицами на ленте. Будем понимать под стандартной конфигурацией конфигурацию, в которой на ленте находится блок из нескольких единиц и машина считывает самую левую единицу из этого блока. Через некоторое конечное число шагов машина останавливается в стандартной конфигурации и на ленте находится блок изmединиц. Число mи будет значением функции fв точкеn. Если машина работает бесконечно долго или останавливается в нестандартной конфигурации, то функция fв точкеnне определена. Мы можем расширить это определение, разрешив принимать mиnзначение ноль. Будем считать, что если машина начинает работу на пустой ленте, то она вычисляет значениеf(0). Если машина заканчивает работу и на ленте нет ни одной единицы, то вычисленное значение функции равно нулю.
Для функций нескольких натуральных переменных расширим это определение. Пусть f(x1,...xk) - функция нескольких переменных область значений которой подмножество натуральных чисел. В этом случае исходная конфигурация - этокблоков единиц. Вi-ом блоке содержитсяxi+1единиц. Нумерация блоков начинается слева. Соседние блоки единиц разделены нулями. Машина считывает самую левую единицу самого левого первого блока. В конечной стандартной конфигурации имеется блок изm+1единиц, гдеm=f(x1,...xk). Если машина не останавливается или останавливается в нестандартной конфигурации, функция не определена на набореx1,...xk.
Примеры невычислимых по Тьюрингу функций
Докажем, что множество функций из натуральных чисел в натуральные несчетно. Будем доказывать это утверждение от противного. Допустим, что наше множество функций счетно. Тогда, все функции из натуральных чисел в натуральные можно расположить в виде спискаf1,...,fk,...и любая функция будет присутствовать в этом списке хотя бы раз. На основе этого списка построим функциюuпо следующему правилу:
{ 1, если fnне определена в точкеn.
u(n)= {
{ fn (n)+1 , еслиfn определена в точкеn.
Функция u(n) из натуральных чисел в натуральные и следовательно должна присутствовать в нашем спискеf1,...,fk,...на некотором местеi , то есть она должна совпадать с некоторой функцией,fiиз нашего списка. И тогда по нашему определению функцииu
{ 1, если fiне определена в точкеi.
u(i)=fi(i)={
{ fi(i) +1 , еслиfi определена в точкеi.
Предположив, что наше множество счетное мы пришли к противоречию. Если функция fiне определена, то по нашему определению она определена и равна 1. Если жеfi определена в точкеi, тоfi(i)= fi(i) +1. И мы получаем равенство 0=1.
Докажем теперь, что множество машин Тьюринга счетно. Любую машину Тьюринга можно описать с помощью множества четверок. Любая четверка - это слово в алфавите0,1,L,R, q1 ,...,qm. Расположим эти слова в алфавитном порядке друг за другом без пробелов между четверками. При этом получится некоторое слово в нашем конечном алфавите, которое описывает машину. Множеству машин Тьюринга будет соответствовать множество слов в нашем конечном алфавите. А ранее мы доказали, что множество слов в конечном алфавите счетно. Следовательно счетно и множество всех машин Тьюринга.
Множество всех функций из натуральных чисел в натуральные несчетно. Множество машин Тьюринга, которые вычисляют эти функции счетно. Отсюда следует, что существуют невычислимые по Тьюрингу функции.
Определим понятие продуктивностимашины Тьюринга. Пусть машинаM, которая вычисляет некоторую функциюf, начинает свою работу на пустой ленте. И останавливается в стандартной конфигурации. Тогда продуктивность машиныM будет равна числу единиц на ленте в момент остановки. Если же машина не остановится или остановится в нестандартной конфигурации, то ее продуктивность равна нулю. Другими словами
{ f(0), если f(0) определена.
продуктивность(M)= {
{ 0 , в противном случае.
Определим теперь функцию p:
p(n)= продуктивность самой продуктивной машины сnсостояниями.
Покажем, что функция pне может быть вычислена ни на одной машине Тьюринга. Для этого определим для начала ряд свойств функцииp.
Покажем,
чтоp(1)=1. Существует бесконечно много
различных машин Тьюринга с одним
состоянием и алфавитом0,1. Но
все эти машины принадлежат 25 различным
классам. Машины одного класса отличаются
друг от друга только именем своего
единственного состояния и ведут себя
совершенно одинаково. Класс от класса
отличается количеством петель в графе
переходов (0,1 или 2) и их маркировкой.
Существует один класс машин с нулевым
числом петель. Машины этого класса
сразу же останавливаются на пустой
ленте, не начав работать. Продуктивность
этих машин равна 0. Машины с двумя петлями
в графе переходов не останавливаются
никогда, потому что независимо от
считываемого символа всегда существует
инструкция которой необходимо следовать.
Таких классов существует 16 , так заполнить
пустые места в маркировках над двумя
дугами0:__ и 1:__
можно 4х4=16 способами. Продуктивность
всех таких машин равна 0.
Дополнительно имеется 8 графов переходов с одной вершиной и одной петлей. Если петля помечена 1:__, то машина останавливается немедленно, так как первоначально на ленте нет единиц. И продуктивность таких четырех классов машин равна 0. Среди оставшихся классов три класса машин не останавливаются никогда. Это машины с петлями “0:R”, “0:L”, “0:0”. Их продуктивность равна нулю. Остался единственный класс машин с петлей “0:1” в графе переходов. Продуктивность машин этого класса равна 1. Итак продуктивность самой продуктивной машины с одним состоянием равна 1.
Докажем неравенство p(47)³100. Построим машину с 47 состояниями, продуктивность которой равна 100. Для этого соединим последовательно машину, которая рисует 25 единиц (пример 1) и две машины из 11 состояний каждая, удваивающие число единиц (примеры 2 и 3). Суммарное число состояний такой машины равно 47, а продуктивность равна 100. Возможно это не самая продуктивная машина с 47 состояниями, но мы можем утверждать, что продуктивность самой продуктивной машины с 47 состояниями больше либо равна 100.
Докажем, что p(n+1)>p(n).
Возьмем произвольную машину из самых продуктивных машин с nсостояниями и добавим к ней еще одно состояние, как на следующем рисунке.
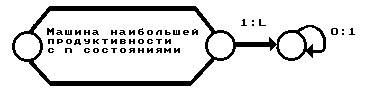
В результате мы получим машину с n+1 состоянием и продуктивностьюp(n)+1. Возможно это не самая продуктивная машина с n+1 состоянием, но неравенствоp(n+1)³p(n)+1мы доказали.
Неравенство p(n+11)³2nследует из примера 3, в котором мы построили машину сn+11 состояниями и продуктивностью2n.
Перейдем теперь к доказательству невычислимости функции p. Это доказательство мы построим от противного. Предположим, что существует машинаBBckсостояниями, которая вычисляет функциюp. Построим машину, граф которой изображен на рисунке, с продуктивностью p(p(n))иn+2kсостояниями.
Если машина BBсуществует, то продуктивность самой продуктивной машины сn+2kсостояниями должна быть не менееp(p(n)). Поэтомуp(n+2k)³p(p(n)). Мы уже доказали, чтоp(n+1)>p(n) для любогоn. Из этого следует, что если BBсуществует, то("n) n+2k³p(n).Если это верно для любого натурального n, то верно и для n+11. Поэтому ("n) n+2k+11³p(n+11), еслиBBсуществует. Мы уже доказали, чтоp(n+11)³2n и поэтому("n) n+2k+11³2n, еслиBBсуществует. Вычитая из обоих частей равенстваn, получим
("n) 2k+11³n, еслиBBсуществует.
В частности это неравенство верно и для n=12+2k. Поэтому2k+11³12+2k , еслиBBсуществует. Или0³1 , еслиBBсуществует. Следовательно наше предположение о существованииBBневерно и функция pневычислима по Тьюрингу.