1. Делимость целых чисел. НОД, НОК и их свойства. Простые числа. Основная теорема теории чисел.

Пусть есть a,bZ

N,Z,Q,R,C – множества чисел

Теорема: о делимости целых чисел

Для любых a,bZ существуют единственные q, r такие, что 0<=r<|b| a=bq+r

q=[a/b] r={a/b}

Если r=0, то a||b (a кратно b)

Теорема 1: Свойства деления

1. a||b, b||c => a||c (транзитивность)

2. a₁,a₂, … ,a_k | => _,_, … ,_k

a_i||c |

^k_i=1a_i_i||c

Если любое а кратно с, то линейная комбинация тоже кратно с

Существует max(a,b)<=M(a,b)<=ab

Определение:

Существует a,b a||d, b||d D(a,b) – НОД

1<=D(a,b)<=min(a,b)

Определение:

a,b называются взаимно простыми, если M(a,b)=1

Теорема 2: Свойства НОД и НОК

1) a₁,a₂, … ,a_k

m||a₁, m||a₂, … , m||a_k m||M(a₁,a₂, … ,a_k) НОД||НОК

Доказательство: Пусть m=M(a₁,a₂, … ,a_k)q+r 0<r<M(a₁,a₂, … ,a_k)

r=m-M(a₁,a₂, … ,a_k)q => r||a₁,a₂, … ,a_k (т.к. m||a₁,a₂, … ,a_k) =>наше предположение неверно r=0

2) a₁,a₂, … ,a_k d₁,d₂, … ,d_k

D(a₁,a₂, … ,a_k)=M(d₁,d₂, … ,d_n)

Доказательство: a_i||d₁, a_i||d₂, … , a_i||d_n т.е. а_i – кратное

a_i||M(d₁,d₂, … ,d_n), M(d₁,d₂, … ,d_n)||d_j

3. ab=D(a,b)M(a,b)

Доказательство: ?????

Пусть есть a₁,a₂, … ,a_k

Как найти D(a₁,a₂, … ,a_k)?

Пусть D(a_i,a_j) известно, тогда

d₁=D(a₁,a₂); d₂=D(d₁,a₃); d_k-1=D(d_k-2,a_k)

Утверждение:

ab||c и (a,c)=1 => b||c

Определение:

а называется простым если а||a или a||1 и у него нет других делителей.

Теорема: 3 Свойства простых чисел.

1. a,p (p – простое) a||p или a||b (b,p)=1

2. ab||p => a||p или b||p

3. a1, существует простой делитель

p=min{d₁,d₂, … ,d_k} – простое

Основная теорема теории чисел Теорема: 4

a=p₁p₂…p_k=p^aq^br^c (p,q,r – простые числа)

Доказательство:

1. a=a₁p₁, если а₁>1, то a₁=a₂p₂

2. Существует единственная комбинация разложения числа на простые сомножители, a=p₁p₂…p_k=q₁q₂…q_k (p,q – простые)

По теореме 3 – p_i||q₁, p_j||q₂

2. Решето Эратосфена. Разложение числа на простые (стандарт­ная схема и метод Ферма).

Нахождение простых чисел в интервале от 1 до N

Алгоритм:

S1 p₁=2, k=1

k+1 P_k

P_k>N остановка, числа можно просматривать до N или до [N]+1

Теорема: 5 Евклида

Множество простых чисел бесконечно

Доказательство: Пусть множество конечно {p₁,p₂…p_k}

Следующее простое число это произведение предыдущих плюс 1, т.е.

p_k+1=p₁p₂…p_k+1

Дано: aZ a=p^aq^br^c…

{p₁,p₂…p_k}

2=p₁<p₂<…<p_k

k,i Step0 k=1, i=1

Step1 a=1 => stop

a=p_kq+r if r=0 => Step3

Step2 r=0 d_i=p_k, i=i+1 => Step1

Step3 r0 k=k+1 => Step1

Алгоритм Ферма

a=xy, a=u²-v²=(u-v)(u+v)

R(u,v)=u²-v²-a остановка при R(u,v)=0

R(u,v)<0 V=V+1

R(u,v)>0 U=U+1

R(u+1,v)=(u+1)²-v²-a=u²-v²-a+(2u+1)=R(u,v)+2u+1

R(u,v+1)=u²-(v+1)²-a=u²-v²-a-(2v+1)=R(u,v)-2u-1

3. Алгоритм Евклида, бинарный алгоритм. Линейное представле­ние НОД.

Алгоритм Евклида

D(a,b) - ?

D(a,b)=D(a-bq,b) a-bq+r

a=bq₀+r₀ D(b,r₀)

b=r₀q₁+r₁ D(r₀,r₁)

r₀=r₁q₂+r₂ D(r₁,r₂)

… … …

r_k-2=r_k-1q_k+r_k D(r_k-1,r_k)

r_k-1=r_kq_k+1

Бинарный алгоритм

1. a,b – четные => D(a,b)=2D(a/2,b/2)

2. a – четное, b – нечетное => D(a,b)=D(a/2,b)

3. D(a,b)=D(a-b,b)

4. a,b – нечетные => a-b – четное

5. |a-b|<max{a,b} a,b>0

S₁ k=0

k=k+1, a=a/2, b=b/2 (пока a,b четные)

S₂ a – нечетное => tmp=-b goto S₄

а – четное => tmp=a

S₃ tmp=tmp/2

S_4a if (tmp – четно) => goto S₃

S₄ if (tmp>0) then a=tmp

Else b=-tmp

S₅ tmp=a-b

Tmp=0 stop

D(a,b)=2^ka

Goto S₃

Пример:

a b tmp

76501 29719 -29719

76501 29719 40782 23391

23391 29719 -6328 -3164 -1522 -791

23391 791 22600 11300 5650 2825

2825 791 2034 1017

1017 791 226 113

113 791 –678 -229

113 339 -226 -113

113. 113

4. Цепные дроби. Разложение числа в цепную дробь. Свойства и вычисление подходящих дробей. (Оба вопроса не разделимы)

5. Бесконечная цепная дробь. Разложение иррациональности в цепную дробь.

Разложение числа в цепную дробь

a>b

. . .

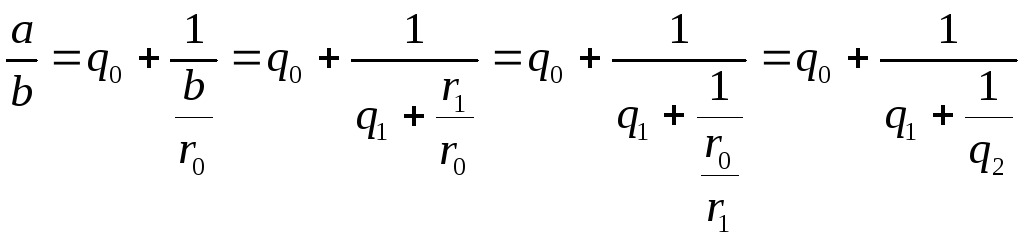
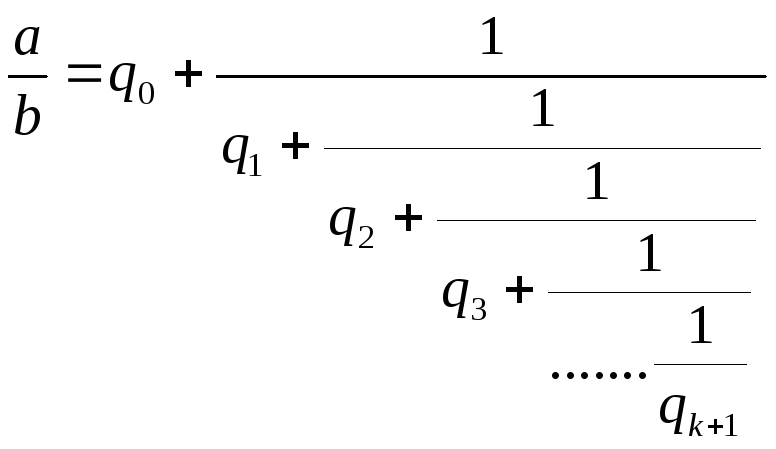
a<b

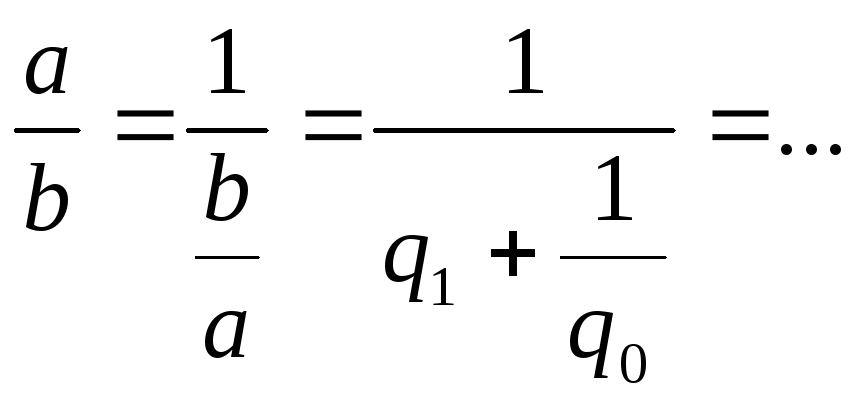
a/b<0

Теорема: 6

Любое рациональное число можно разложить в цепную дробь, одним и только одним способом, где все q_i>0, i>=1, a последнее q_k>1

(Если q_k не >1 то 2 разл: (q₀,q₁,…,q_k-1,1)

ZR имитируем алгоритм Евклида для вещественного числа

Z=q₀+₁ q₀=[Z] – выделим целую часть числа

_(0,1), Z₁>1

Z=q₀+1/Z₁ (разложение числа в цепную дробь)

Z₁=q₁+₂ q₁=[Z₁]

_(0,1)

Z₁=q₁+1/Z₂, Z₂>1

Z₂=q₂+₃

….

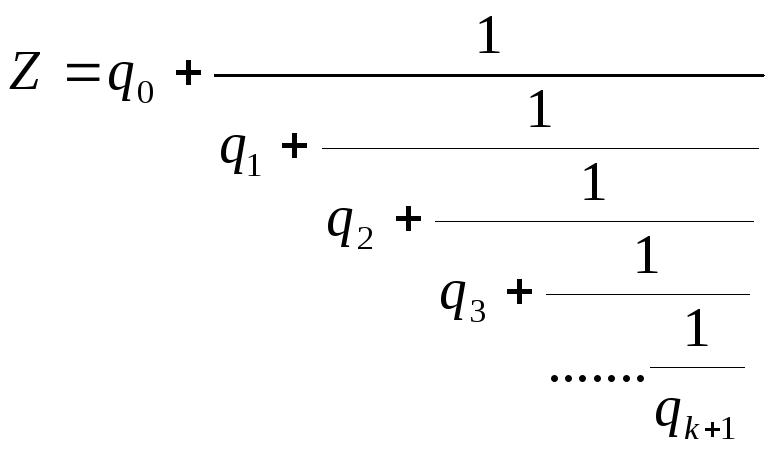=q₀,q₁…q_k+1

Пример:

(5,(3,2,10)) т.е. цепная периодическая дробь

Вычисление подходящих дробей

_k=-P_k/Q_k – подходящая дробь

Найдем формулы для вычисления P_k Q_k

Вводим условную дробь _=1/0 т.е. P_-1,Q_-1=0

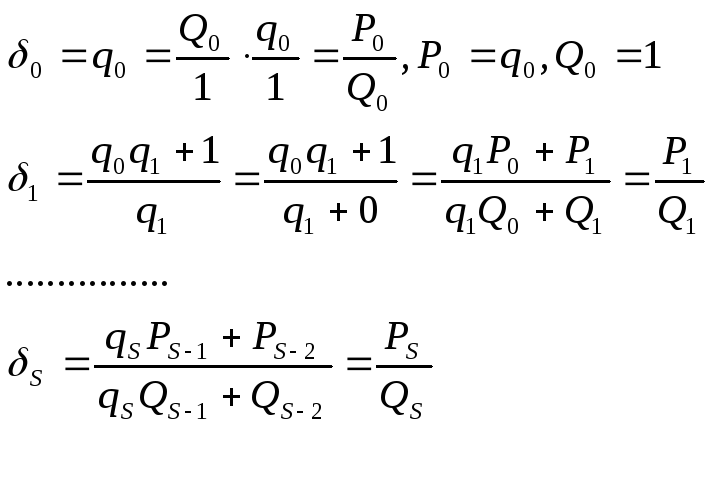
		1	2	3	4	5	6	7	8
Qs		2	1	1	2	1	6	1	4
Ps	1	2	3	5	13	18	121	139	677
Qs	0	1	1	2	5	7	47	54	263

h_s=P_sQ_s-1-Q_sP_s-1

(q_sP_s-1+P_s-2)Q_s-1-(q_sQ_s-1+Q_s-2)

P_s-1=P_s-2Q_s-1-Q_s-2P_s-1=-(Q_s-2P_s-1-P_s-2Q_s-1)=-h_s-1

h_s=-h_s-1=(-1)²h_s-2=…=h₀(-1)^s

h₀=-1, h_s=(-1)^s+1

;

Q_-1=0; Q₁=1; Q₂=q₂Q₁+Q₀ (последующие Q_i монотонно возрастают)

h_s=(-1)^S+1=(Q_s-1P_s-P_s-1Q_s)

P_sQ_s || d делятся на d=1

D(P_s-2,Q_s)=1 взаимно просты

R

=q₀+₁ q₀=[]

_=q₁+₂ q₁=[_]



_S=q_S+_S+1

подпоследовательность нечетных дробей убывает

подпоследовательность четных дробей возрастает

;

=(5,(3,2,3,10)) =5,29150267

0,0001 1/Q_S²<0,0001 => Q_S>100

		1	2	3	4	5	6	7
Qs		5	3	2	3	10	3	2
Ps	1	5	16	37	127	1037	4018	9403
Qs	0	1	3	6	24	247	465	1777

16/3=5,3(3)

37/7=5,2857

127/24=5,2915

1037/247=5,2915

6. Решение диофантовых уравнений.