6. Максимум перерегулирования при невозрастающей вчх (рис.5)

рисунок 5

представим интеграл (5) в виде ряда:

Представленный ряд является знакопеременным и сходящимся, т.к. его члены при увеличении Х стремятся к 0, убывая по абсолютному значению. Т.к.сумма всех членов знакопеременного сходящегося ряда не превышает значение первого члена, то

.

Это неравенство можно усилить, если вместо поставить ,т.е.

при любом t. Тогда или или Т.о., если ВЧХ представляет собой невозрастающую функцию , то перерегулирование переходного процесса на превышает 18% (свойство малых перерегулирований)

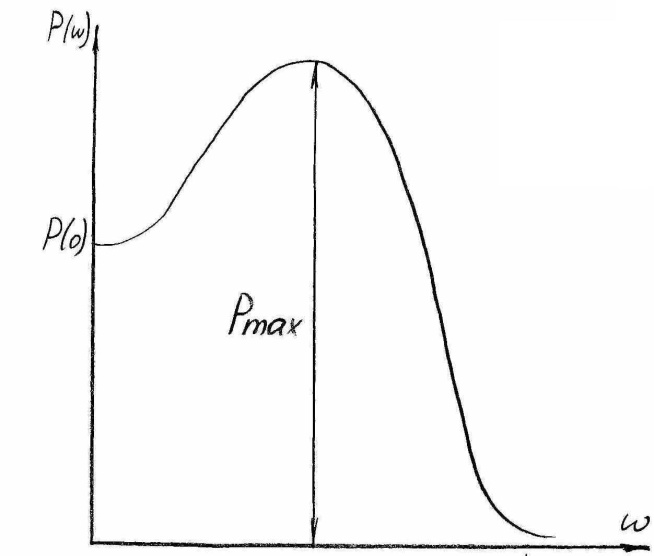
7. Зависимость максимума перерегулирования от максимума ВЧХ P_max.

а) б)

Рисунок 6

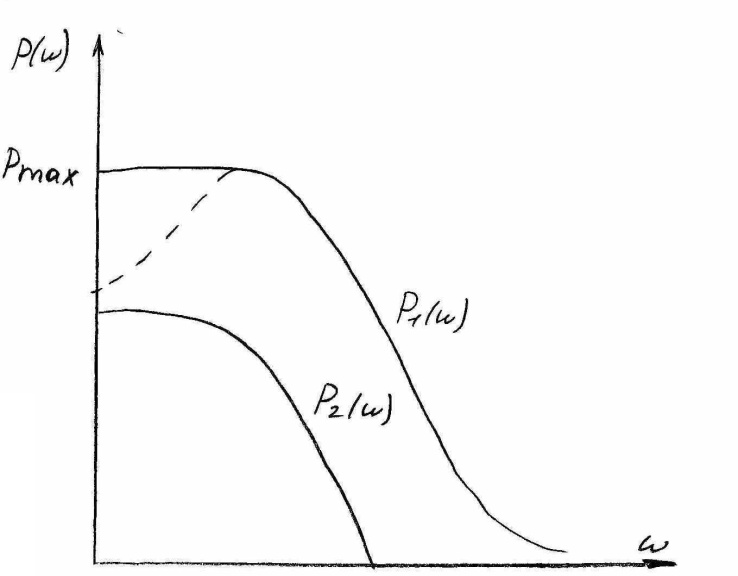
На рис 6(а) показана ВЧХ, имеющая максимум и удовлетворяющая условию . Очевидно, что такую ВЧХ можно представить в виде разности двух характеристик (рис 6 (б)), тогда на основании (5) будем иметь:

Учитывая, что второй интеграл всегда положителен (?) будем иметь , т.к. функция удовлетворяет свойству (6), то при любом t. Заменяя h(t) на h_max и учитывая равенство будем иметь:

Если например , то перерегулирование , т.о. при увеличении максимума ВЧХ максимум перерегулирования также растёт.

8. Зависимость между устойчивостью системы и непрерывностью ВЧХ.

На перерегулирование и следовательно на колебательность переходного процесса оказывает влияние не только положительный, но и отрицательный максимум ВЧХ. Чем больше эти максимумы, тем больше колебательность процесса (рис 7 кривая 1).

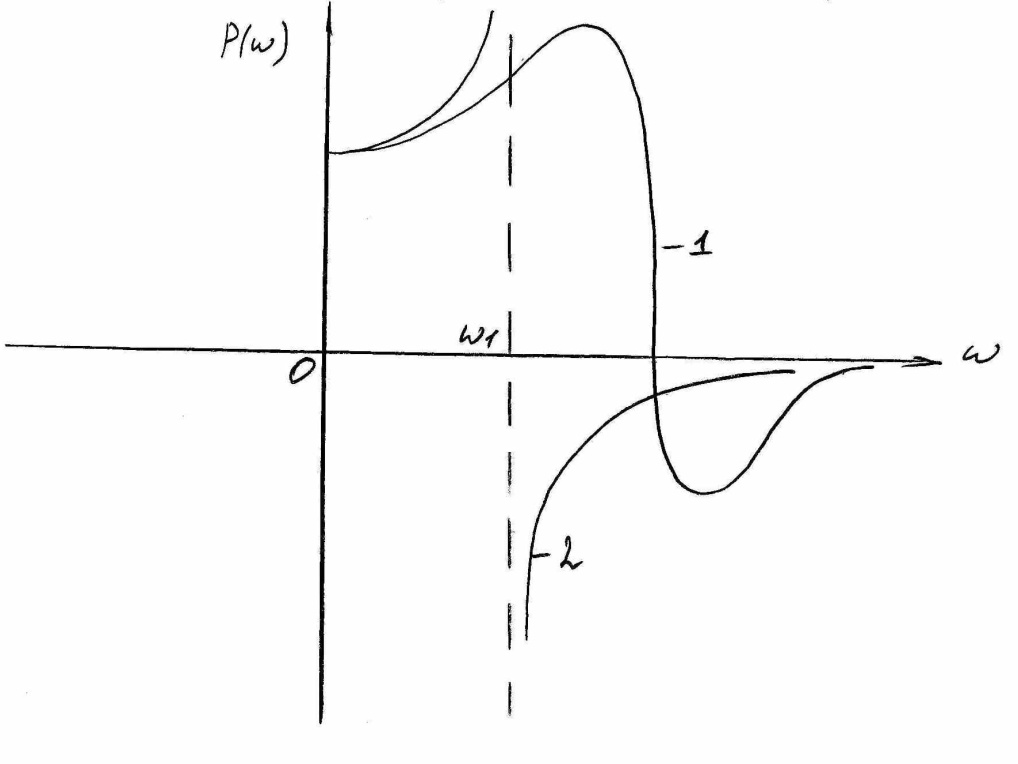
Рисунок 7

Если ВЧХ в точке , терпит разрыв непрерывности (кривая 2), то система при находится на границе устойчивости. Действительно, учитывая, что КЧХ замкнутой системы определяется , то формула для определения ВЧХ может быть представлена в виде:

,

где характеристический вектор замкнутой системы (смотри критерий Михайлова). Очевидно, что ВЧХ обращается в только в том случае, когда вектор и обращается в 0, т.е. в случае, когда имеются сопряжённые мнимые корни . Т.о. наличие сопряженных мнимых корней на границе устойчивости и существование в системе незатухающих колебаний.

В) Оценка качества переходного процесса по АЧХ замкнутой системы . Складывая уравнение (5) и (6) будем иметь:

Учитывая, что и , а также:

и

после элементарных преобразований имеем:

Т.о. о качестве переходного процесса можно судить по частотным характеристикам замкнутой системы.

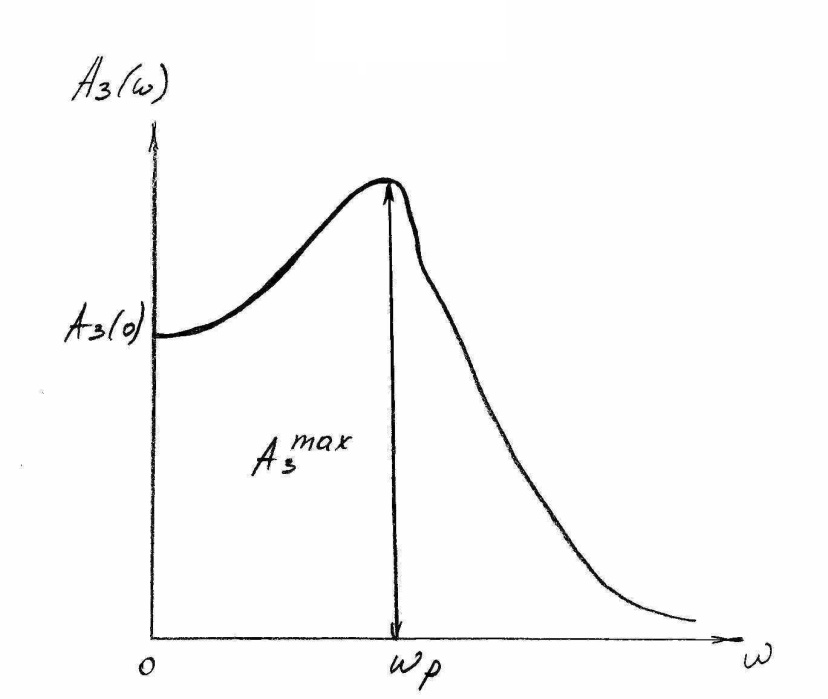
Рисунок 8

Рассмотрим АЧХ замкнутой системы (рис 8). При гармонических воздействиях качество переходных процессов оценивается по показателю колебательности М, который представляет собой отношение максимального значения АЧХ к её начальному значению при как было установлено выше для астатических САР , а для статических САР . Если значение к велико (к»1), то и для статических систем можно принять , тогда , где ω_р-резонансная частота. При этой частоте гармонические колебания проходят через систему с наибольшим усилением.

Показатель колебательности М характеризует склонность системы к колебаниям. Действительно, АЧХ замкнутой системы определяется так:

(7)

где W(jω)- АФХ разомкнутой системы.

Следовательно при некоторой частоте ω_к:

(8)

Эта АФХ показана на рисунке 9 (кривая 1).

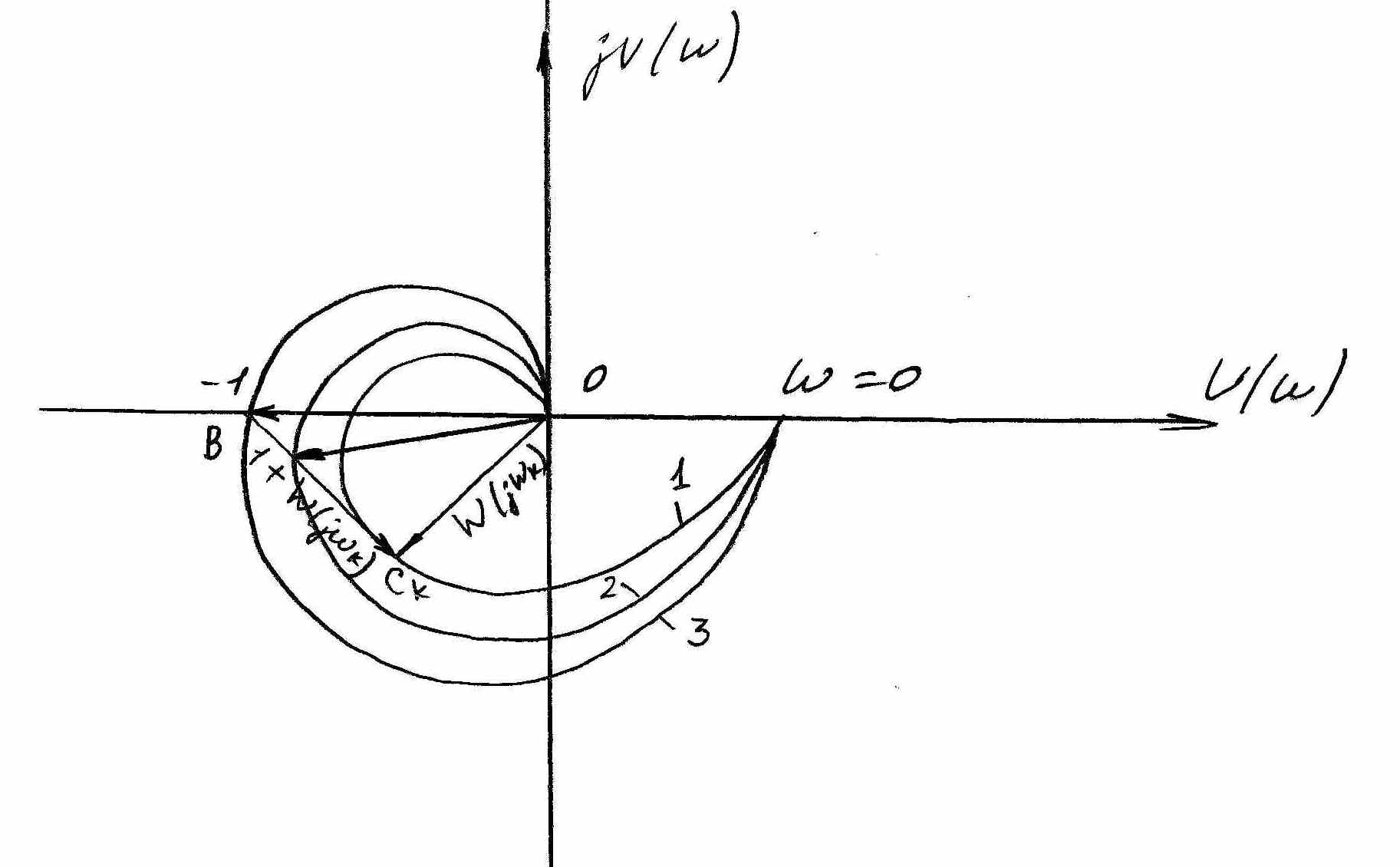
Рисунок 9

Т.о. АЧХ замкнутой системы можно получить по кривой АФХ разомкнутой системы, определяя отношения (8) для различных значений частот. Максимальное из этих отношений и есть показатель колебательности:

(9)

Из уравнения (9) следует, что чем ближе АФХ разомкнутой системы подходит к точке В (-1;j0) (кривая 2), тем меньше отрезок ВС_к и тем больше будет отношение(9), а следовательно показатель колебательности М₂›М₁.

Если АФХ при некоторой частоте ω₁ проходит через точку В (кривая 3), то отрезок ВС_к становится =0 и А₃(ω) достигает максимума = ∞, т.е. и замкнутая система находится на границе устойчивости, совершая незатухающие колебания (смотри свойство (8) ВЧХ).

Т.о. чем выше величина М, тем система более склонна к колебаничм, тем меньше зоны устойчивости, т.е. менее качественна система припрочих равных условиях.

Считается, что в хорошо демпфированных системах показатель колебательности М=1,1-1,5. Величину М можно определить по АФХ разомкнутой системы W(jω), если нанести на неё график линии М=const. Полагая, что W(jω)=U(ω)+jV(ω) то на основании формулы (7) будет иметь:

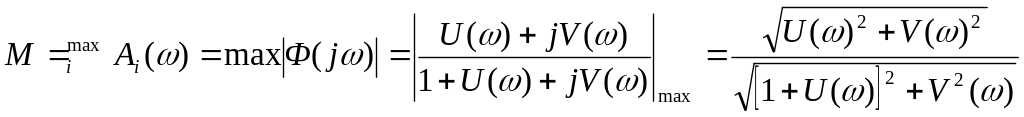
Возведя обе части равенства в квадрат будем иметь:

После алгебраических преобразований будем иметь:

или

Это выражение представляет собой уравнение окружности радиусом , центр которой смещён относительно начала координат влево на расстояние . Задаваясь различными значениями М от 0 до ∞, можно построить семейство окружностей (рисунок10).

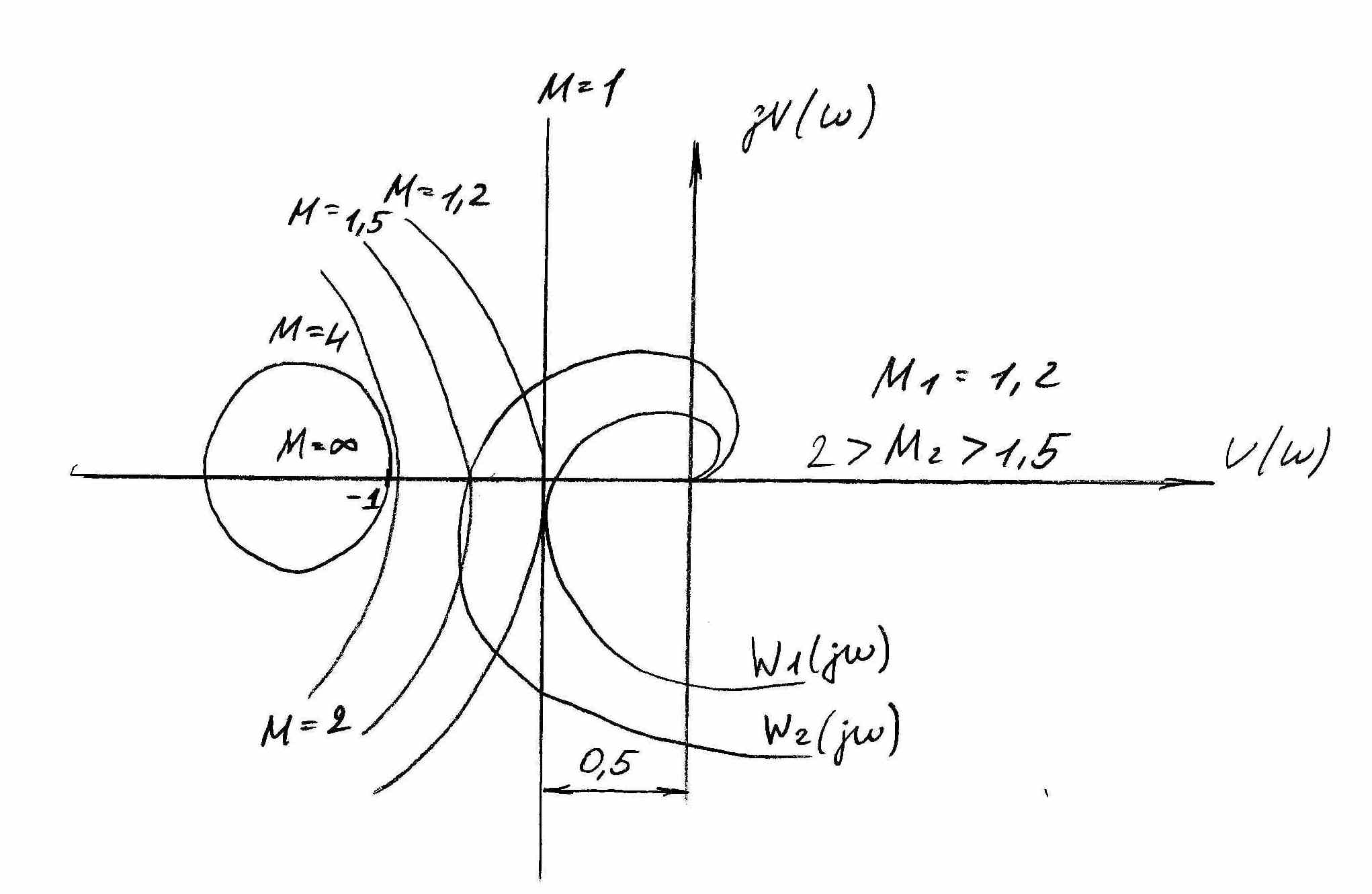
Рисунок 10

При М=1 окружность вырождается в прямую линию (R→∞, C→∞) параллельную мнимой оси и проходящую слева от неё через точку с координатами (-0,5; j0):

Если М→∞, то окружность вырождается в точку с координатами (-1; j0).

Окружность, построенная для заданного М является границей области. Если АФХ разомкнутой системы входит в эту область, то показатель М системы будет больше заданного. Если АФХ касается этой окружности, то М равно заданному. Например для двух систем с АФХ W₁(jω) и W(jω) будем иметь М₁=1,2; 2>М₂>1,5. Следовательно, система 1 обладает хорошими динамическими характеристиками, а система 2 имеет ________ колебательный переходный процесс. Т.о. для того, чтобы показатель М замкнутой системы был не более заданного необходимо и достаточно чтобы АФХ не пересекала окружность, построенную для М заданного.

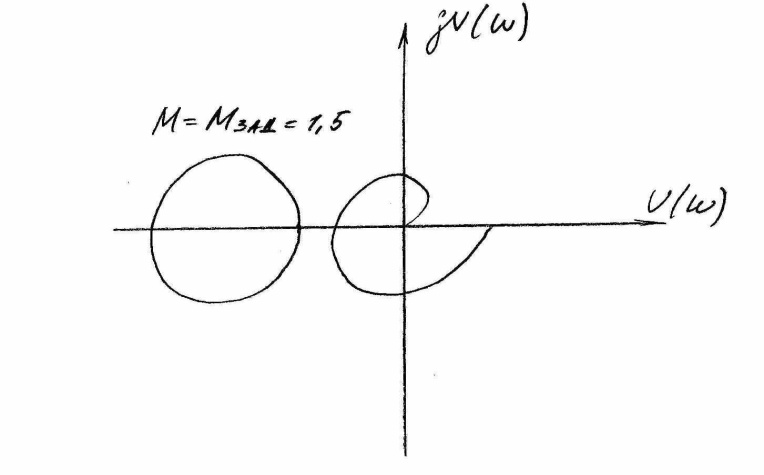
Показателю М соответствует резонансная частота ω_р,которая обычно приближённо равна частоте колебаний замкнутой системы в переходном процессе, При этом время достижения первого максимума можно приближённо определить . При условии, что переходный процесс заканчивается за 1-2 колебания(это соответствует М=1,1-1,3), время регулирования приближённо оценивается .

Г) Определение ВЧХ замкнутой системы по частотным характеристикам разомкнутой системы

КЧХ замкнутой системы , полагая W(jω)=U(ω)+jV(ω) будем иметь:

Отсюда

(10)

Выражение (10) позволяет найти на плоскости W(jω) геометрические места точек соответствующие постоянным значениям вещественной Р(ω)=Р=const и мнимой Q(ω)=Q=const частотных характеристик. Т.о.

После ряда преобразований это выражение приводится к виду:

(11)

Выражение (11)представляет собой уравнение окружности радиусом , центр которой находится на вещественной оси в точке . На рисунке 11 показаны окружности, построенные для различных значений Р=const. Все окружности проходят через точку -1 на оси абсцисс. Окружность, соответствующая Р=1 имеет бесконечно большой радиус и представляется прямой, параллельной оси ординат и расположенной слева от неё на расстояние =1.

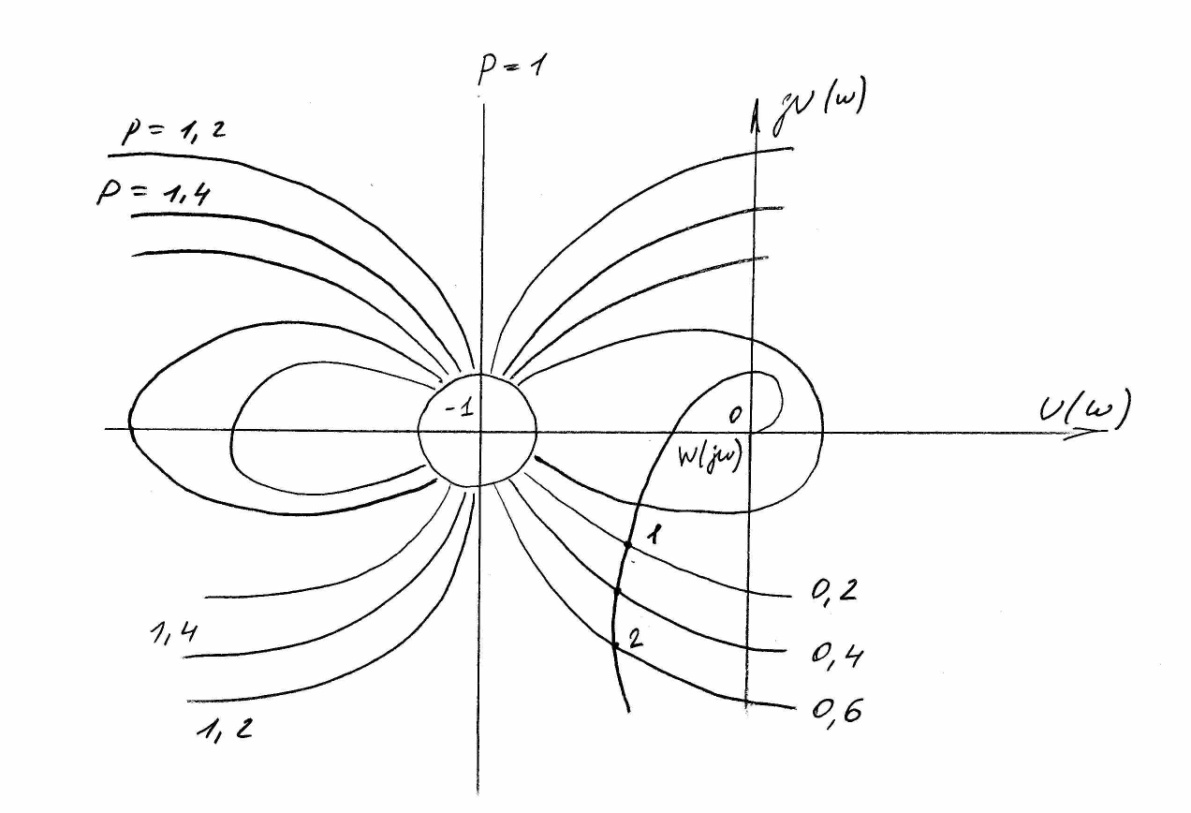
Рисунок 11

Диаграммы, представленные на рисунке 11, называются круговыми.

Для определения ВЧХ на круговую диаграмму накладывают АФХ разомкнутой системы, выполненную в том же масштабе, и рассматривают точки её пересечения с окружностями. Каждая точка пересечения соответствует определённой частоте ω_i, которую устанавливают по АФХ и ординате ВЧХ замкнутой системы Р(ω_i) при этой частоте, равной индексу окружности. Например для точки 1 имеем частоту ω₁, которой соответствует значение ВЧХ Р(ω₁)=0,2. Для точки 2 имеем ω₂, Р(ω₂)=0,6.

ВЧХ замкнутой системы может быть определена и по ЛЧХ разомкнутой системы. Учитывая, что КЧХ может быть представлена замкнутой, тогда

Откуда:

;

;

;

.

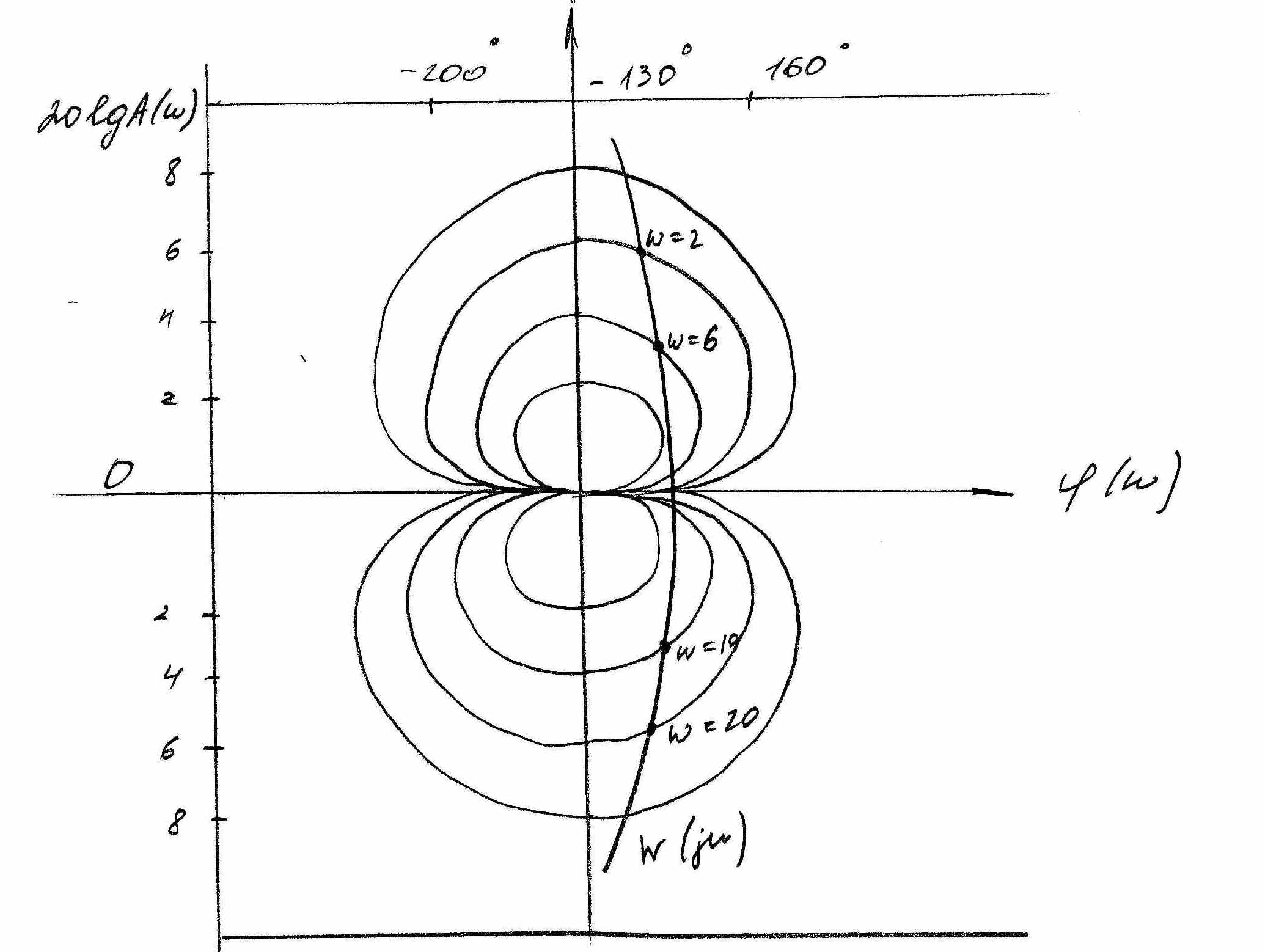
Рисунок 12.

На рисунке 12 приведена номограмма ,построенная для ВЧХ и представляющая собой линии ровных значений Р в координатной плоскости, где по оси ординат откладывают 20lgА(ω), а по оси абсцисс фазу φ(ω).

Если заданы ЛАХ и ЛФХ, то, пересекая значения амплитуды и фазы при разных частотах на плоскость номограммы, получают АФХ разомкнутой системы в координатах номограммы, Точки пересечения с линиями ровных значений определяют ω₂ и соответствуют Р(ω₂)= индексу кривой номограммы, на которой лежит рассмотренная точка пересечения.

Определим по формуле (12) значение Р(ω), соответствующее частоте среза системы. В результате можно определить значения частоты среза по ВЧХ замкнутой системы.