§ 3. Частотные методы оценки качества

Используя преобразование Фурье можно установить связь между переходным процессом и частотными характеристиками системы. На этом основаны частотные методы оценки качества процессов регулирования.

Частотный метод позволяет оценить показатели переходного процесса, если заданы или экспериментально определены частотные характеристики разомкнутой и замкнутой системы. Вместе с тем частотный метод дает возможность построить переходный процесс без выявления корней.

А) Зависимость между переходной функцией n(t) и частотной характеристики замкнутой системы.

По формуле обратного преобразования Фурье:

(1).

Уравнение (1) определяет переходный процесс через частотные функции системы и внешнего воздействия x(t). Область применения выражения (1) ограничена (слово непонятное), когда y(t) является полностью интегрируемой функцией, т.е. удовлетворяет условию: . Это условие выполняется у всех устойчивых САР для свободной с переходной составляющей y_своб(t) переходного процесса, который является затухающей функцией времени, а следовательно несобственный интеграл от неё является конечным (см § 3.1)

Рассмотрим определение с помощью частотных характеристик переходной функции где .

Согласно вышеизложенному формулой (1) можно выразить только свободную составляющую , функции h(t), т.к. в общем случае сама функция h(t) не является абсолютно интегрируемой.

Учитывая, что изображение является свободной составляющей h_своб(t)

или

, где , т.к. Q(0)=0.

Принимая во внимание, что , получаем следующее выражение для ПФ:

(2).

Подставляя в уравнение (2) выражения:

и , будем иметь:

Учитывая, что h(t) является вещественной функцией, то два последних интеграла будут равны 0, тогда:

Учитывая, что второй интеграл называется интегральным синусом:

,

а также, то что подынтегральные функции двух других интегралов являются четными функциями ω будем иметь:

(3).

Учитывая, что функция при t<0 и подставляя в уравнение (3) вместо t, -t будем иметь:

(4).

Вычитая из уравнения (3) уравнение (4) получим соотношение между ПФ и ВЧХ замкнутой системы:

(5)

Складывая уравнения (3) и (4) получим соотношение между h(t) и МЧХ:

(6)

Уравнения (5) и (6) явно показывают, что характер переходного процесса зависит от частоты характеристик системы, находя производную выражения (5) по времени получим весовую функцию системы:

Б) Оценка качества переходного процесса по ВЧХ.

ВЧХ замкнутой системы обладают некоторыми свойствами, которые позволяют судить о качестве переходного процесса непосредственно по самой характеристике. Рассмотрим некоторые из них:

1. Начальное значение Р(0) зависит от того является ли система статической или астатической: ПФ разомкнутой статической системы может быть представлен в виде:

Где - общий коэффициент передачи разомкнутой системы Очевидно, что ,

тогда начальное значение ВЧХ:

Для астатической системы ПФ имеет вид , где - ПФ статической части системы, не имеющей астатических звеньев (интегрирующих), тогда для замкнутой системы:

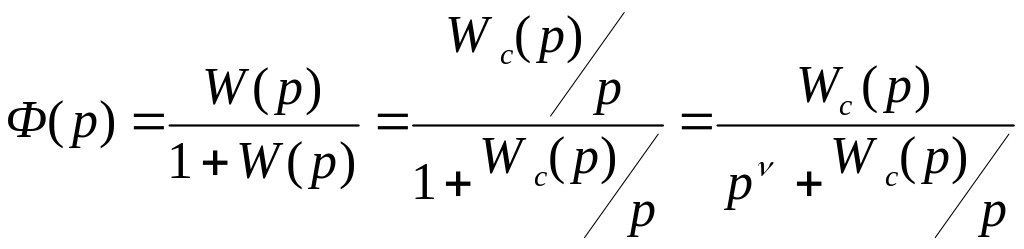
Тогда начальное значение ВЧХ Р(0)=Ф(0)=1 т.о. ВЧХ статической САР имеет начальное значение <1, а ВЧХ астатической САР имеет начальную ординату всегда =1. (рис. 3.)

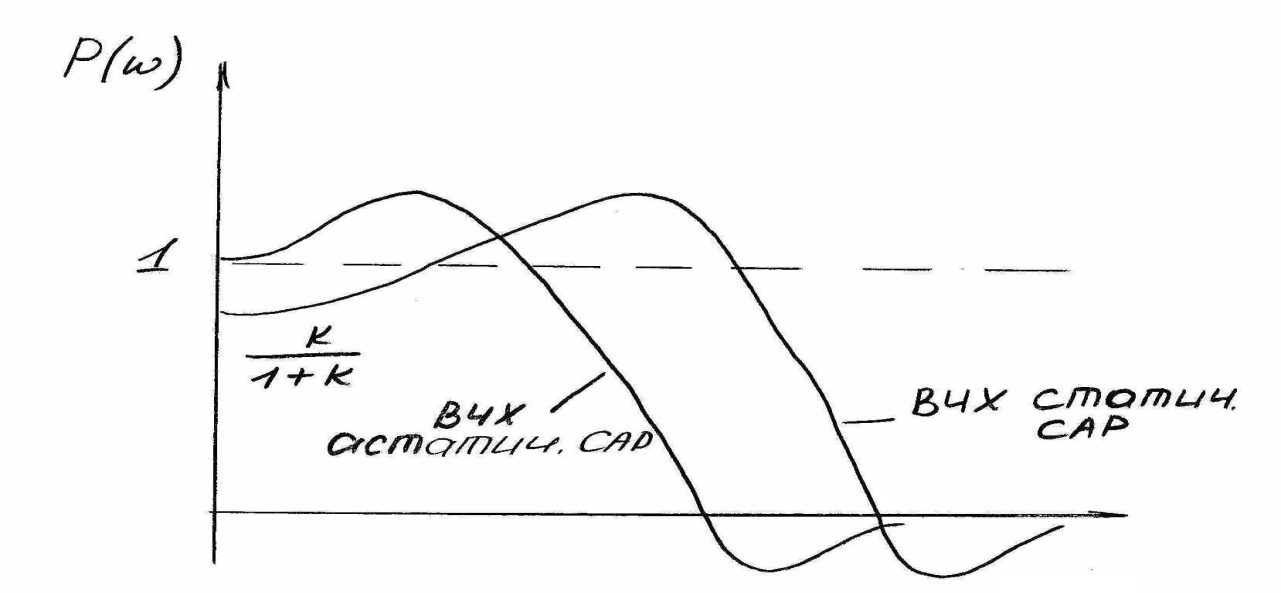
Рисунок 3

2. Установившееся значение переходного процесса.

Применяя теорему о конечном значении оригинала, будем иметь:

3. Начальное значение переходного процесса.

Применяя теорему о начальном значении оригинала получим:

Или после замены

Если у ПФ Ф(р): m<n , то , m<n, то , если m=n, то

4. Изменение масштаба по оси ординат.

Если изменить масштаб ВЧХ по оси ординат в n раз, то масштаб кривой переходного процесса изменится в тоже число раз. Действительно умножая обе части уравнения (5) на n будем иметь:

Это свойство показано на рис. 4 (а), (б)

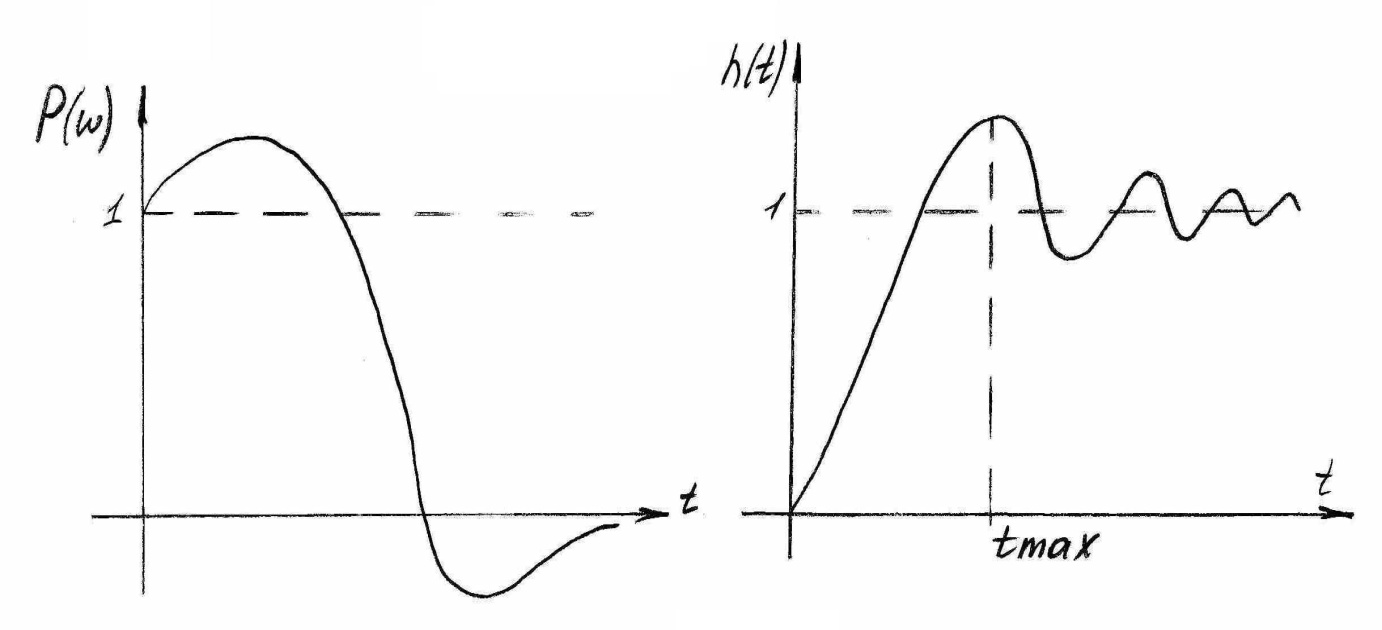
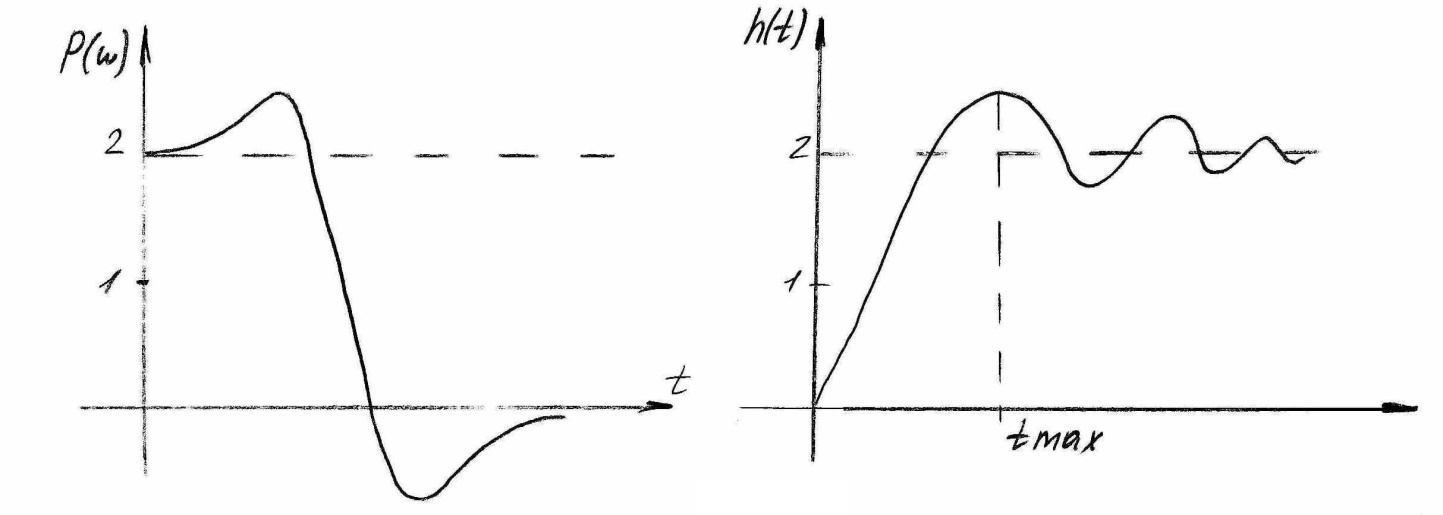
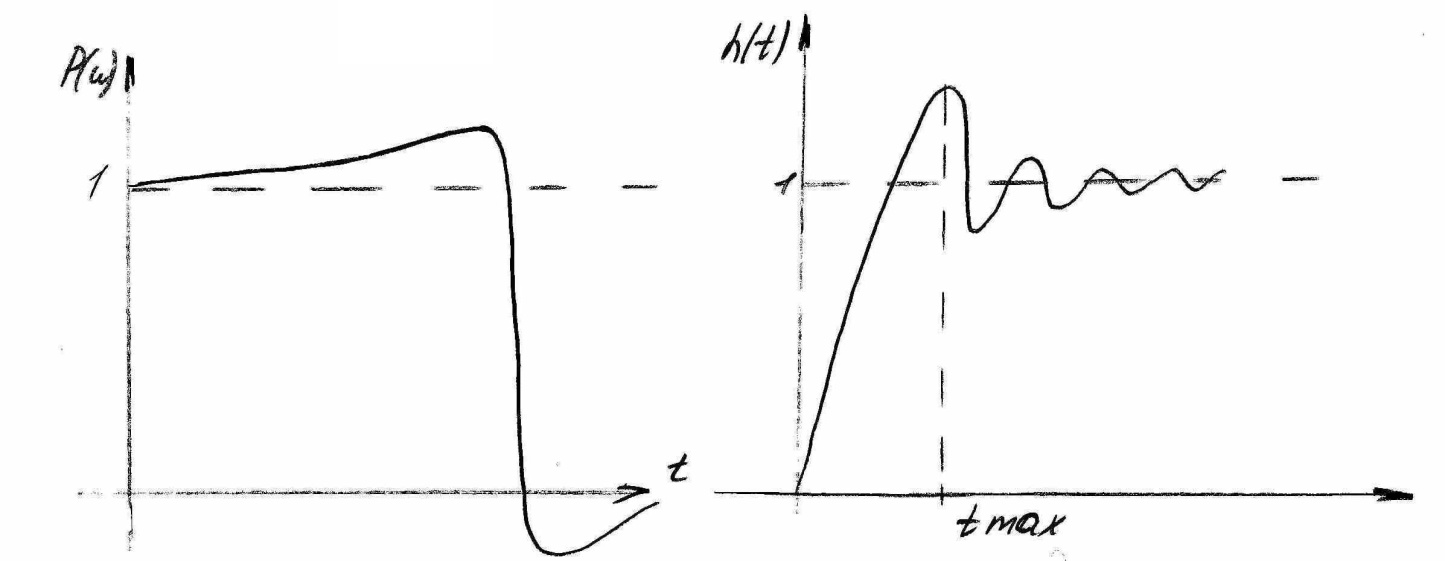
рисунок 4

5. Изменение масштаба по оси абсцисс.

Если увеличить(уменьшить) в n раз масштаб аргумента ВЧХ, то масштаб аргумента кривой переходного процесса уменьшится(увеличится) в тоже число раз. Обозначим переходный процесс, обусловленный изменением масштаба аргумента ВЧХ в n раз через Вводя новую переменную получим:

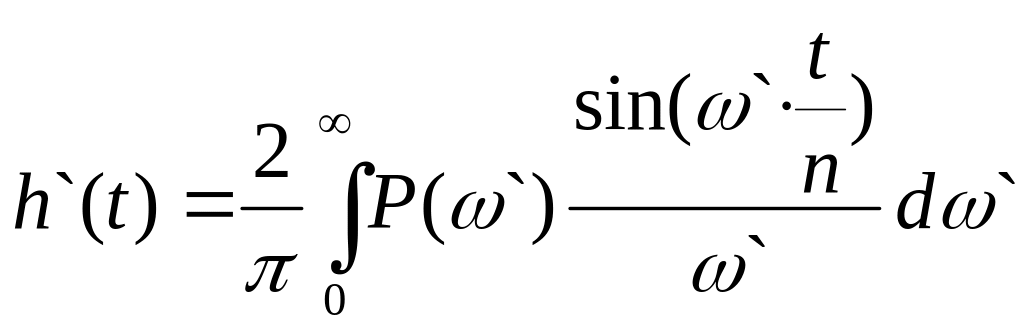
Учитывая последнее равенство и уравнение (5) получаем или

Т.о. более широкому графику ВЧХ соответствует более быстрый переходный процесс, и наоборот. Это свойство показано на рис. 4 (в). Ему можно дать и физическое объяснение, если учесть .