5. Передаточные функции разомкнутых систем.

Исследование динамических свойств ИС удобно производить на основе анализа их ПФ-й. Рассмотрим существо и методику определения ПФ-й импульсных систем с различными структурными схемами.

1. Линейная система с ИЭ на входе.

Рассмотрим разомкнутую ИСв состав которой входят ПИЭ, ФЭ с ПФ-й и непрерывная часть (НЧ), свойства которой описываются ПФ-й (рис 1а).

Рисунок 1( а , б)

Обычно для удобства структурных исследований ФЭ относят к НЧ.

Образованный таким образом элемент называется приведенной непрерывной частью ПНЧ ИС с ПФ-й .

Из рисунка 1б следует, что на входе ПНЧ действует последовательность модулированных по площади S-импульсов, то есть сигнал . В связи с тем, что в ИС и в САР присутствуют сигналы обоих типов (непрерывные и дискретные) то анализ таких систем существенно усложняется. Учитывая, что Z-преобразование оперирует только с дискретными функциями необходимо все непрерывные сигналы рассмотреть лишь в дискретные моменты времени nT. Получаемая при этом погрешность сравнима с погрешностью при решении дифференциальных уравнений численными методами. Для этого факта на схему наносят фиктивные ИЭ, которые обозначают пунктирными линиями.

Связь между непрерывной выходной ПНЧ y(t) и дискретной входной величиной в изображениях по Лапласу имеет вид

Таким образом изображение по Лапласу выходного сигнала ПНЧ определяется произведением ПФ-и ПНЧ и Z-изображения «входного» сигнала ИС g(nT).

Учитывая это определим ПФ-ю разомкнутой системы (рис 1(б)). Для этого подвергнем специальному Z-преобразованию правые и левые части полученного равенства

откуда

(1)

ПФ-я W(z) связывает в рассматриваемой ИС Z-изображение входного и выходного сигналов и называется дискретной ПФ-й разомкнутой ИС.

Таким образом чтобы найти функцию W(z), состоящей из последовательного соединения РНЭ и НЧ, нужно найти ПФ-ю ПНЧ, а затем определить ее Z-изображение.

Рассмотрим пример определения дискретной ПФ-и разомкнутой системы импульсной НЧ которая предстваленя интегрирующим звеном

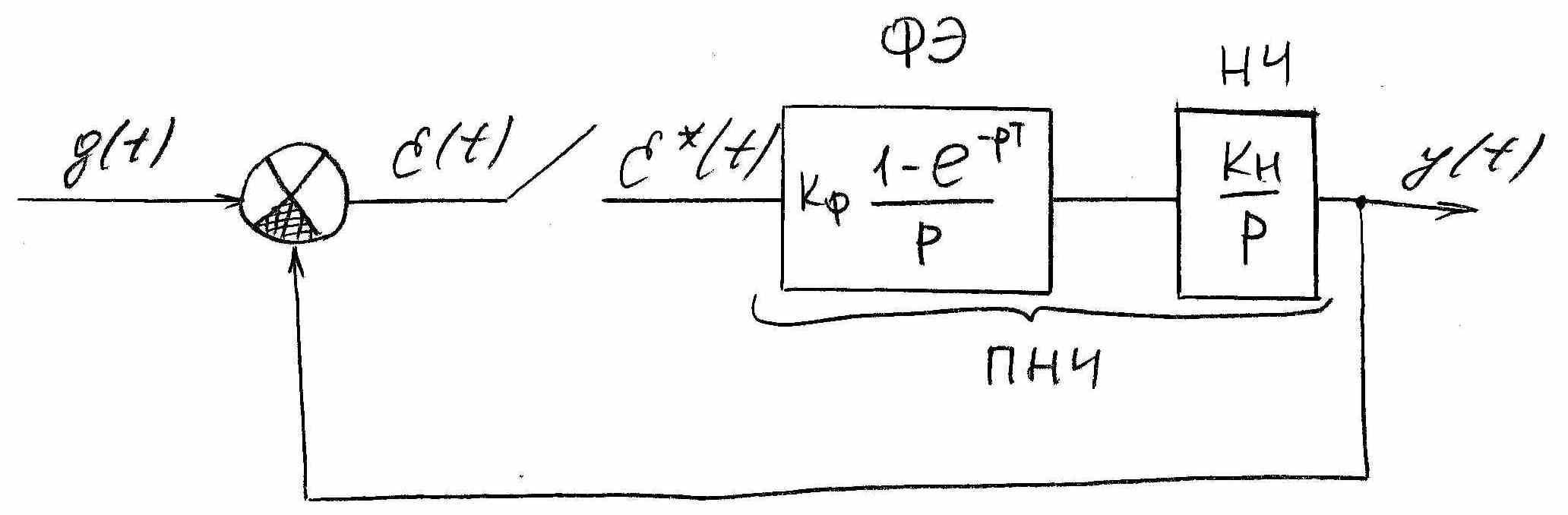
ПФ-я ПНЧ

, где - общий коэффициент передачи.

Учитывая, что получаем дискретную ПФ-ю разомкнутой системы

, где X(p)- изображение по Лапласу некоторой функции времени X(t).

По специальным таблицам получаем

Тогда

Тогда окончательно дискретная ПФ-я ИС

, где M(z), K(z) некоторые опереторные полиномы от некоторой комплексной величины Z (z- оператор преобразования).

Очевидно, что ПФ-я W(z) имеет один полюс , откуда следует, что =0, что соответствует нахождению разомкнутой системы на границе устойчивости.

2. Последовательное соединение 2-х непрерывных частей с импульсными элементами на входах

В этом случае (рис 2) имеем

Рисунок 2

В этом случае имеем

Выполняя специальное Z-преобразование будем иметь

Исключая промежуточную переменную X(z) получим , откуда

Таким образом дискретная ПФ-я системы W(z) определяется как производная дискретных ПФ-й , , причем они определяются как Z-преобразование от соответсвующих непрерывных ПФ-й ,

3)Последовательное соединение 2-х непрерывных частей с одним импульсным элементом на входе.

В этом случае (рисунок 3) справедливы следующие соотношения

Рисунок 3

Применяя специальное Z-преобразование к получим

отсюда следует, что дискретная ПФ-я

Таким образом если 2 НЧ нераздельны ИЭ, то дискретная ПФ-я система W(z) не равна произведению дискретных ПФ-й этих двух НЧ

4)Последовательное соединения 2-х непрерывных частей разделенных импульсным элементом

Рисунок 4

Для этого случая (рис 4) уравнение, созывающее между собой величины в изображениях

Выполняя специальное Z-преобразование будем иметь: из 1-го уравнения и из второго уравнения откуда следует, что изображение выходной величины системы

Из этого равенства следует, что изображение выходного сигнала Y(z) и входного сигнала G(z) НС на рис. 4 не имеют связи через какую-либо ПФ-ю W(z) так как в правой части уравнения нет сомножителя G(z). Это объясняется тем, что сигнал g(t) подвергается функциональному преобразованию НЧ-ю стоящей перед ПИЭ. Несмотря на это получив изображения выходной величины можно от него перейти к оригиналу и тем самым иметь возможность анализировать качество системы.