17. Структурные средние, их графическое определение.

Особым видом средних величин являются структурные сред­ние.

Величина средней определяется всеми значениями признака, встречающимися в данном ряду распределения. Различают такие структурные средние, как:

1. мода

2. медиана

3. квартиль

4. дециль

5. перцентиль

Мода

Это значение признака, которое встречается в ряду распределения чаще, чем другие его значения.

В дискретном ряду распределения значения моды определяются визуально. Для интервального ряда распределения с равными интервалами мода определяется по следующей формуле:

В интервальном вариационном ряду медиана вычесляетс по формуле:

Медиана

Это центральное значение признака, им обладает центральный член ранжированного ряда.

Прежде всего определяется порядковый номер медианы по формуле и строят ряд накопленных частот. Накопленной частоте, которая равна порядковому номеру медианы или первая его превышает, в дискретном вариационном ряду соответствует значение медианы, а в интервальном – медианный интервал.

Для интервального ряда медиана рассчитывается по следующей формуле:

• нижняя граница медианного интервала,

• величина медианного интервала,

• сумма частот (весов) ряда,

• сумма накопленных частот (весов) в интервале, предшествующем медианному,

• частота медианного интервала.

Квартиль

Первый квартиль вычисляется по формуле:

• нижняя граница квартильного интервала,

• величина квартильного интервала,

• номер квартильного признака,

• сумма накопленных частот (весов) в интервалах, предшествующих квартильному,

• частота квартильного интервала.

Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.

Дециль

Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.

18. Показатели вариации Вариация - это колеблемость признака около средней величины. Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и квартильное отклонение.

Размах вариации (R) — есть разность между наибольшим (Xmax) и наименьшим (Xmin) значениями признака в ряду распределения: R = Xmax – Xmin. По величине размаха вариации можно судить о различии между передовыми и отстающими. Однако этот пок-ль имеет тот сущ-й недостаток, что он полностью зависит от отдельных случаев, оказавшиеся на обоих полюсах ранжированного ряда. Между тем, отдельные случаи не всегда достаточно характерны, и опора на них может дать превратное предст-е о характере колеблимости. Поэтому возникает необход-ть в другом показателе, кот-й опирался бы не на одни только крайние значения, а и на значения опред-го признака в данной совок-ти. Среднее линейное отклонение (d_cp) представляет собой среднюю величину отклонений значений признака от их средней величины. При его расче­те все отклонения берутся со знаком плюс. Бывает простое: d_cp =  (x – x_cp) / n и взвешенное: d_cp =  (x – x_cp)f / f. Дисперсия, или средний квадрат отклонений вариантов признака от их средней величины (G²), вычисляется по формулам: простая G² =  (x – x_cp)² / n; взвешенная G² = ( (x – x_cp)² * f ) / f. Затем возвращаясь к линейному измерению, надо из величины дис­персии извлечь квадратный корень и мы получим наиболее точный пока­затель - среднее квадратическое отклонение: простое G =  (x – x_cp)² / n и взвешенное G² = ( (x – x_cp)² * f ) / f. В отличие от среднего линейного и среднего квадратического откло-нения коэффициент вариации является мерой относительной колебле­мости признака около средней величины и характеризует степень одно­родности признака в изучаемой совокупности. Он определяется по формуле: V = G / x_cp * 100%. Если коэффициент вариации > 33,3 %, исследуемая совокупность счи­тается неоднородной и должна быть разгруппирована. По величине коэффициента вариации можно судить о степени вариа­ции признаков совокупностей. Чем больше его величина, тем больше раз­брос значений признаков вокруг средней, тем менее однородна совокуп­ность по своему составу и тем менее представительна средняя

19. Дисперсия, свойства дисперсии.

Дисперсия – представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины:

В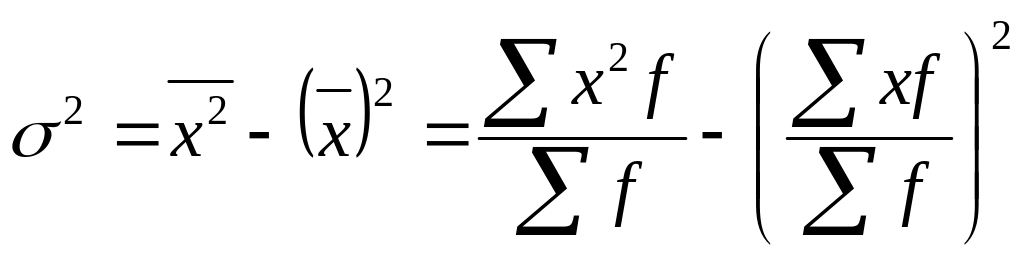 иды дисперсии: 1) общая дисперсия изм-т вариацию признака всей совокупности под влиянием всех факторов, обуславливающих эту вариацию, 2) межгруп.дисперсия отражает вариацию результативн.признака под влиянием фактор.признака положенного в основание груп-ки

3 ) средняя внутригруп.дисперсия отражает случайн.вариацию под влиянием неучтенных факторов и независимых от признака фактора

П равила сложения дисперсии применяются: для оценки точки выборки (серийной и типической), в дисперсионном анализе, для расчета коэф-та детерминации и эмперич.корреляц.отн-ния.

Р асчет дисперсии может быть упрощен. В случае равных интервалов в вариационном ряду распределения используется способ отсчета от условного нуля (способ моментов). Для его понимания необходимо знать математические свойства дисперсии.

Свойства дисперсии

Дисперсия постоянной величины равна нулю.

Уменьшение всех значений признака на одну и ту же величину А не меняет величины дисперсии:

^2(х-A) = ^2x .

Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по их отклонениям от какого-то постоянно числа.

Уменьшение всех значений признака в k раз уменьшает дисперсию в k раз, а среднее квадратическое отклонение – в k раз:

^2(х/A) = ^2x : k .

Значит, все значения признака можно разделить на какое-то постоянное число (скажем, на величину интервала ряда), исчислить среднее квадратичное отклонение, а затем умножить на постоянное число:

^2х > ^2х/k k .

Если исчислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (х), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической:

^2A > ^2х .

Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней и этой условно взятой величины, т.е. на (x - A)^2 :

Значит, средний квадрат отклонений равен среднему квадрату значений признака минус квадрат среднего значения признака.

20. Способ моментов

Способ моментов Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1. Если возможно, то уменьшаются веса.

2. Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом.

3. Находятся отклонения вариантов от условного нуля.

4. Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель.

5. Находится среднее значение признака по следующей формуле