

Задача 14
( Стохатрон − ускоритель заряженных частиц )
Для получения заряженных частиц высоких энергий используются специальные электрофизические установки – ускорители заряженных частиц. Обычно увеличение энергии частиц в ускорителях происходит за счет ускоряющего электрического поля, которое, как правило, стараются создать таким образом, чтобы частица каждый раз увеличивала свою энергию при прохождении области с электрическим полем. Однако, как показано ниже, возможно и стохастическое ускорение заряженных частиц, когда электрическое поле может как ускорять, так и замедлять пролетающие частицы случайным образом. Такие ускорители получили название
стохатронов.
Рассмотрим ускоритель электронов, состоящий из вакуумной камеры, внутри которой движутся частицы, из магнитной системы, поле которой заставляет частицы двигаться по траектории, близкой к окружности, и из
|
|
|
ускоряющего промежутка − двух пластин, |
||||||
|
|
|
к |
которым |
приложена |
разность |
|||
|
|
|
электрических потенциалов, принимающая |
||||||
|
|
|
случайным |
образом значение |
+ U |
или |
|||
|
|
U |
− U . |
При каждом обороте, пролетая зазор |
|||||
e |
- |
|
между пластинами, |
электрон |
будет |
||||
|
|
приобретать |
энергию |
∆E = ±eU |
в |
||||
|
|
|
|||||||
|
|
|
|||||||
|
|
|
зависимости |
от |
того, какое |
было |
|||
напряжение на зазоре в момент его прохождения электроном. Поскольку все реальные магнитные системы и вакуумные камеры обеспечивают лишь ограниченную область пропускания по энергии частиц, будем считать, что электрон погибает на стенках вакуумной камеры, внутри которой он движется, если его энергия меньше некоторой минимальной энергии Emin
или больше некоторой максимальной энергии Emax . Будем также считать, что электроны инжектированы (введены) в вакуумную камеру ускорителя с
59

начальной энергией Ein и в дальнейшем движутся в ускорителе в виде короткого по длине пучка частиц.
Смоделировать работу стохатрона и убедиться, что такая система может служить ускорителем электронов в смысле увеличения средней энергии пучка заряженных частиц.
1. Построить график зависимости средней энергии E электронов в пучке
ускорителя от числа |
n |
прохождений пучка через ускоряющий зазор с |
|||
разностью потенциалов |
U = 500 кВ, если начальная энергия электронов |
||||
Ein = 100 МэВ, |
минимальная и максимальная энергия, |
соответственно, |
|||
Emin = 90 МэВ |
и |
|
Emax = 250 МэВ. |
Рекомендуемое начальное |
|
количество частиц в пучке для моделирования − 1000 . |
Для сравнения |
||||
построить аналогичный график для случая, когда на ускоряющий зазор приложена одна и та же разность потенциалов + U .
2. Построить график зависимости числа N частиц в электронном пучке от
конечной средней энергии E частиц. Показать уменьшение количества частиц в такой системе из-за их потерь на стенках вакуумной камеры. Найти, какая часть частиц останется в пучке, когда средняя энергия электронов будет 150 МэВ, 200 МэВ ?
Дополнительные вопросы:
а) Для графика средней энергии электронов в пучке как функции числа прохождений через зазор предположить аналитический вид зависимости. Методом наименьших квадратов найти параметры этой зависимости.
б) Через заданное число k прохождений пучком ускоряющего зазора предусмотреть вывод гистограммы распределения электронов по энергии. Нанести на гистограмму линии, соответствующие минимально и максимально возможной энергии электронов. Предположить вид зависимости, которая бы неплохо аппроксимировала получаемые гистограммы.
60
в) Как изменятся результаты моделирования, если при прохождении ускоряющего зазора пучком электронов разность потенциалов на зазоре может принимать случайное значение, равномерно распределенное в интервале от − U до + U ?
д) Указать видимые недостатки стохастического метода ускорения заряженных частиц по сравнению с другими, более широко используемыми методами.
Задача 15
( Многократное комптоновское рассеяние )
Рентгеновские кванты падают слева на бериллиевую пластину толщиной
D = 10 см. |
Средняя длина свободного пробега квантов в бериллии |
λ = 2.5 см. |
После пробега длиной λ квант с вероятностью pt = 0.15 |
поглощается |
в веществе или с вероятностью ps = 0.85 рассеивается. |
Считать рассеяние квантов изотропным по углу, изменением энергии квантов при рассеянии пренебречь. Рассмотреть движение квантов в пластине с помощью метода Монте-Карло в двумерном (плоском) приближении.
1. Нарисовать картину траекторий квантов при прохождении пластины. Выделить точки поглощения квантов.
2. Найти вероятности: pпрох − прохождения пластины квантом; pпогл −
поглощения кванта в пластине; pрас − выхода кванта назад из пластины при рассеянии.
3.Построить гистограмму распределения квантов по углу вылета при их выходе из пластины и объяснить качественно результаты.
Дополнительные вопросы:
а) Учесть, что реальное комптоновское рассеяние квантов неизотропно по углу и в двумерном случае описывается плотностью вероятности
61

p(ϑ) = 31π (1+ cos2 ϑ) , где угол ϑ рассеяния отсчитывается от
направления распространения кванта перед рассеянием.
Как изменятся предыдущие результаты с учетом анизотропности рассеяния квантов ?
б) Рассмотреть трехмерный случай распространения квантов в пластине, считая, что рассеяние кванта аксиально симметрично вокруг направления его движения перед рассеянием, а вероятность его рассеяния на угол ϑ относительно этого направления описывается плотностью вероятности
p(ϑ) = 163π (1+ cos2 ϑ)sin ϑ . Картину траекторий квантов рисовать в
проекции на плоскость сечения пластины.
Насколько сильно изменятся результаты задачи по сравнению с двумерным случаем ?
Задача 16
( Ядерный реактор )
Исследовать условия работы гомогенного (однородного) уран-
графитового ядерного реактора в виде квадрата со стороной |
a . В |
начальный момент времени в реакторе находится n = 30 |
нейтронов, |
случайно распределенных по реактору. Средняя длина свободного пробега нейтрона до взаимодействия с каким-нибудь ядром равна λ = 1.7 см. При взаимодействии с ядром возможно:
− |
с вероятностью |
ps = 0.9632 − изотропное рассеяние нейтрона; |
|
− |
с вероятностью |
pa |
= 0.0152 − поглощение нейтрона без деления ядра; |
− |
с вероятностью |
p f |
= 0.0216 − поглощение нейтрона с делением ядра |
урана.
При делении ядра урана в среднем вылетает n = 2.47 нейтрона.
62
Смоделировать работу реактора на основе метода Монте-Карло. Считать, что нейтроны живут в реакторе поколениями, и число поколений пропорционально времени, а нейтроны до взаимодействия с каким-нибудь ядром пробегают одинаковое расстояние λ . Также считать, что, если число нейтронов превышает 500 , то реактор взрывается; если же число нейтронов становится равным 0 , то реактор гаснет. Стенки реактора − без отражающих свойств.
1. Построить график зависимости количества нейтронов в реакторе от времени при заданном размере реактора a .
2. Оценить критический размер реактора acr .
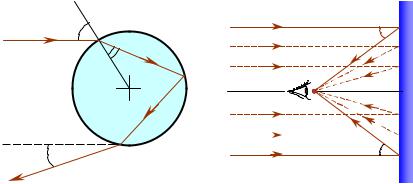
3. Рассмотреть такой же реактор, но с формой в виде круга радиусом a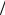 2 .
2 .
Оценить для него критический размер и сравнить с критическим размером для квадратного реактора.
Задача 17
( Радуга )
Радуга − одно из удивительных и прекрасных явлений природы, поэтому люди издавна пытались понять, как она возникает. Сначала итальянец Антонио Доминико (1566-1624), а затем Исаак Ньютон (1643-1727) смогли правильно указать физический механизм образования радуги [9]. Согласно этим представлениям, радуга возникает в результате попадания в глаз наблюдателя солнечных лучей, испытавших двукратное преломление и одно отражение в дождевой капле (см. рисунок). Если световой луч испытает внутри капли два последовательных отражения, а затем выйдет из нее, то может наблюдаться вторичная радуга, расположенная выше основной и имеющая обратное чередование цветов по отношению к основной радуге.
Методом Монте-Карло исследовать возникновение радуги при рассеянии света на сферической капле воды. При моделировании считать, что световые лучи от Солнца случайно и равномерно (по поперечному
63
ϕ |
солнечные лучи |
|
|
γ |
я |
||
|
|||
от Солнца |
|
д |
|
ψ |
ж |
||
|
|||
γ |
γ |
с т е н а д о |
|
|
|
||
к наблюдателю |
|
|
сечению капли) попадают на каплю, испытывая дальше преломления и отражения. Учесть, что преломление лучей на границе раздела сред происходит согласно закону Снеллиуса sin ϕ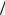 sin ψ = n , где углы
sin ψ = n , где углы
падающего (ϕ) и преломленного (ψ) луча отсчитываются от нормали к границе раздела, а n − относительный показатель преломления среды, в которой распространяется преломленный луч, относительно среды, в которой распространяется падающий луч. Зависимость показателя преломления воды
от длины волны |
λ света может быть описана выражением: |
|
n = 1.322 + |
3905 |
, где λ выражена в нанометрах. |
|
λ2 |
|
1. Построить гистограммы распределения интенсивности рассеянного света от угла γ , отсчитываемого от начального направления световых лучей, для синего (400 нм), зеленого (550 нм) и красного (650 нм) света. Считать, что никаких потерь лучей в процессах преломления и отражения не происходит. Рассмотреть случаи одного и двух отражений внутри капли. Определить области углов γ , в которых наблюдается разделение цветов. Выяснить, каким входящим в каплю лучам соответствуют эти области углов.
64
2.В действительности при прохождении светом границы раздела сред возникают и преломленный, и отраженный лучи. Для неполяризованного
света зависимость коэффициента отражения R от границы раздела имеет вид
sin2 |
(ϕ − ψ) |
+ |
tg2 |
(ϕ − ψ) |
|
||
R = 0.5 |
2 |
(ϕ + ψ) |
tg |
2 |
|
, |
|
sin |
|
|
|
(ϕ + ψ) |
|
||
и, соответственно, коэффициент пропускания равен T =1− R . Это означает, что при прохождении границы раздела сред каждый фотон с вероятностью R может отразиться от границы и с вероятностью T пройти через границу.
Рассмотреть процесс рассеяния света каплей для случаев одного и двух отражений внутри капли с учетом коэффициентов отражения и пропускания. Как изменятся результаты моделирования по сравнению с предыдущим случаем ? Оценить интенсивность цветов во вторичной радуге по отношению к первичной.
Задача 18
( Случайные блуждания и уравнение теплопроводности )
Стационарное распределение температуры в заданной области при отсутствии источников тепла описывается уравнением Лапласа (см. ПРИЛОЖЕНИЕ)
∂ 2T |
+ |
∂ 2T |
+ |
∂ 2T |
= 0 |
|
∂x2 |
∂y 2 |
∂z 2 |
||||
|
|
|
при заданных условиях на границе T |Г = T0 (x, y, z).
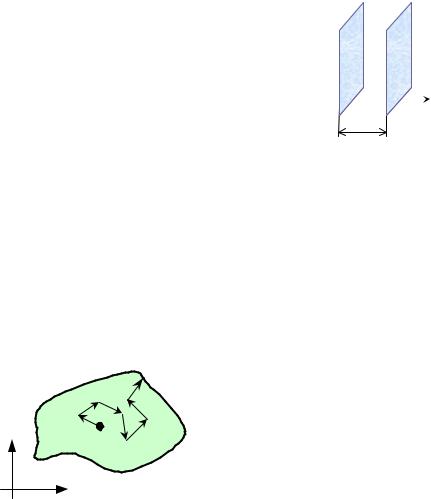
В некоторых случаях решение этого уравнения может быть найдено аналитически. Например, в случае, когда у нас имеется две бесконечные
плоскости с разными температурами T1 и T2 , разнесенные на расстояние a , уравнение Лапласа превращается в одномерное
65
∂ 2T |
= |
d 2T |
= 0 |
|
|
|
|
|
|
|
|
|
|
∂x2 |
dx2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
с граничными условиями |
T (0) |
= T , |
T (a) = T . |
T1 |
T2 |
||||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
Решением |
|
последнего |
|
уравнения |
|
является |
|
|
x |
||||
|
|
|
|
|
|
(T2 − T1) x |
|
|
|
||||
линейная функция T (x) |
= |
|
+ T1 . |
|
|
|
|
||||||
|
|
|
|
|
|||||||||
|
|
a |
|
|
|
a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Для двумерной или трехмерной задачи с |
|
|
|
|
|||||||||
произвольными граничными |
условиями не |
|
|
|
|
||||||||
всегда возможно найти аналитическое решение |
T (x, y) или |
T (x, y, z) , но |
|||||||||||
существует много методов численного решения. |
|
|
|
|
|||||||||
Рассмотрим здесь интересный численный способ решения уравнения теплопроводности для двумерного случая, основанный на методе статистического моделирования. Этот способ особенно хорош, когда не требуется высокая точность результатов, или когда решение нужно найти
только для какой-то ограниченной области внутри всей области задания. |
|
||||||
|
|
|
Рассматриваемый |
способ |
|||
|
|
|
основан на аналогии уравнений |
||||
|
Г |
Ti=T0(xi,yi) |
теплопроводности |
и |
диффузии |
||
|
(случайного |
или |
броуновского |
||||
|
|
|
|||||
|
G |
|
движения |
частиц). |
Пусть |
||
y |
|
имеется некоторая |
область |
G , |
|||
|
(x,y) |
|
окруженная |
границей Г |
с |
||
|
|
|
|||||
|
x |
|
заданным |
распределением |
|||
|
|
температуры |
на |
границе |
|||
|
|
|
T |Г = T0 (x, y). Выберем внутри |
||||
области какую-нибудь точку (x, y) , в которой мы хотим найти значение температуры T (x, y) . Одну за другой будем выпускать частицы из этой точки, и пусть дальше каждая из них движется случайным образом с
некоторым шагом |
s |
. Рано или поздно частица пересечет границу области в |
некоторой точке |
i , |
в которой температура равна Ti = T0 (xi , yi ) . Выпустив |
66

таким образом |
из точки |
(x, y) |
N |
частиц, |
получим |
N |
значений |
||||||
граничных температур |
Ti , |
где |
i = 1, |
, N . |
Тогда за |
приближенное |
|||||||
значение температуры в точке |
(x, y) |
можем принять среднее значение по |
|||||||||||
всем полученным граничным температурам: |
|
|
|
|
|
||||||||
T (x, y)≈ |
1 |
N |
T = |
1 |
N T (x |
, y ) . |
|
|
|
|
|
||
N |
∑ |
N |
|
|
|
|
|
||||||
|
i |
∑ |
0 i |
i |
|
|
|
|
|
|
|||
|
|
i =1 |
|
i =1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
По-другому, если рассмотреть это в обратном направлении по времени, |
|||||||||||||
то имеем следующую |
картину: |
каждая |
из |
N |
частиц |
приобретает |
|||||||
некоторую температуру на границе области и, двигаясь случайным образом, приносит эту температуру в выбранную точку (x, y) .
Для получения правдоподобных решений необходимо, чтобы величина
шага s свободного пробега |
частиц была много меньше характерных |
размеров заданной области G . |
Очевидно также, чем больше частиц будет |
выпущено из выбранной точки (x, y) , тем точнее найденное значение температуры в этой точке будет приближать точное решение.
1. Найти рассмотренным способом распределение температуры между двух бесконечных плоскостей, находящихся на расстоянии a друг от друга. Температуры плоскостей равны T1 и T2 , соответственно.
Методом наименьших квадратов убедиться, что полученная
зависимость удовлетворяет виду T (x) = |
(T2 |
− T1) x |
+ T1 . |
|
a |
||
|
|
|
2.Имеется квадрат со стороной a , на границах которого заданы следующие температуры:
T0 |
(x) = − sin(πx a) sh(π 2) , |
на нижней границе |
y = −a / 2 |
; |
T0 |
(x) = sin(πx a) sh(π 2) , |
на верхней границе |
y = a / 2 |
; |
T0 |
( y) = − sh(π y / a) , |
на левой границе x = −a / 2 ; |
|
|
T0 |
( y) = sh(π y / a) , |
на правой границе |
x = a / 2 . |
|
67
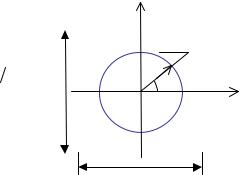
а) Построить график распределения |
|
|
|
|
|
|
y |
|
||||||||||
температуры |
на |
окружности, |
центр |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
a/π |
|
|
||||||||
которой совпадает с центром квадрата, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и радиус которой |
равен |
R = a π . |
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
ϕ |
|
|
|||||||||
a |
|
|
|
|
|
|
|
|||||||||||
Построение |
графика |
производить |
в |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
полярных |
координатах |
в |
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|||
T = T (ϕ) , где ϕ |
изменяется от 0 до |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
2π . Какой вид имеет график ? |
|
|
|
|
|
|
|
a |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
б) Найти распределение температуры T (x, y) |
по всей области внутри |
|||||||||||||||||
квадрата. |
Вывести |
полученное |
распределение |
псевдоцветами, |
разбив |
|||||||||||||
полный диапазон температур |
(Tmax − Tmin ) на 16 градаций. |
|
||||||||||||||||
в) Для предыдущего случая произвести вывод найденного распределения в виде трехмерного графика T (x, y) .
Задача 19
( Классический обнаружитель сигналов )
Для решения задачи обнаружения сигнала ns на некотором фоновом уровне nf в смеси nsf = n f + ns при априорной (до проведения опыта)
неопределенности в наличии сигнала в смеси применяют прием, называемый критерием Неймана-Пирсона. Суть его заключается в следующем. Устанавливаются две вероятности ошибочных решений − вероятность ложной тревоги α и вероятность пропуска сигнала β . Вероятности α и
β выбирают достаточно маленькие (как правило, 0.05 и менее), чтобы не очень часто пропускать сигнал, когда он есть, и, наоборот, не поднимать зря тревогу, когда сигнала нет. Для заданных α и β определяются две величины: T − время измерения и M − порог, с которым сравнивают
68
