
ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ-КАРЛО
Метод Монте-Карло, будучи случайным по своей природе, применяется также и для решения многих задач, не связанных с какими-либо случайностями. В частности, он используется при решении ряда задач вычислительной математики, например, для вычисления интегралов (особенно высокой кратности).
Пусть у нас есть некоторая функция y = f (x) и необходимо вычислить определенный интеграл от этой функции на интервале (a,b) :
b
I = ∫ f (x) dx .
a
Разработано много разных методов вычисления интегралов с помощью статистического моделирования. Рассмотрим здесь лишь два наиболее простых.
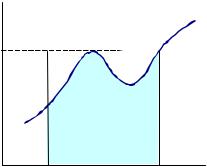
Первый метод аналогичен способу определения площади произвольной плоской фигуры, описанному выше.
|
|
|
Рассмотрим |
прямоуголь- |
||||
f(x) |
|
ник |
со |
сторонами |
|
x = a , |
||
|
x = b , |
y = 0 и y = M , где |
||||||
|
|
|||||||
M |
|
M − число, равное или превы- |
||||||
|
|
шающее по величине макси- |
||||||
|
|
мум |
функции |
на |
интервале |
|||
|
|
(a,b) , так что 0 ≤ f (x) ≤ M |
||||||
|
|
на всем интервале (см. рис.). |
||||||
0 |
x |
Будем |
заполнять |
этот |
||||
b |
прямоугольник |
случайными |
||||||
a |
||||||||
|
|
точками |
(ξ,η) , координаты |
|||||
которых равномерно распределены в интервалах |
a < ξ < b , |
0 < η < M . |
||||||
Тогда геометрически |
очевидно, что |
приближенное |
значение |
интеграла |
||||
39
(заштрихованная на рисунке площадь) будет равно |
площади |
S0 |
||||||||||||||||||
прямоугольника, |
умноженной на отношение числа точек N ′ |
, попавших под |
||||||||||||||||||
кривую |
y = f (x) |
, к общему числу точек N . Следовательно: |
|
|
||||||||||||||||
|
|
b |
|
|
|
N ′ |
|
|
|
|
|
|
N ' |
|
|
|
|
|
|
|
|
I = ∫ f (x) dx |
≈ S0 |
|
= M |
(b − a) |
|
. |
|
|
|
|
|
|
|||||||
|
N |
|
|
|
|
|
|
|
||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На практике это означает, что для каждой разыгранной точки |
(ξi ,ηi ) , |
||||||||||||||||||
где |
i = 1,2, |
, N |
, проверяется условие |
ηi < f (ξi ) , и, если оно выполнено, |
||||||||||||||||
то в счетчик для |
N ′ добавляется единица, |
в противном случае − ничего не |
||||||||||||||||||
добавляется. |
После проведения |
N |
испытаний по приведенной формуле |
|||||||||||||||||
вычисляется приближенное значение интеграла. |
|
|
|
|
|
|||||||||||||||
|
Аналогично могут быть вычислены и кратные интегралы. Например, |
|||||||||||||||||||
для |
двойного |
интеграла |
от |
функции |
|
f (x, y) |
|
|
по |
области |
||||||||||
G = {a < x < b, |
c < y < d } будем иметь |
|
|
|
|
|
|
|
|
|||||||||||
|
I = ∫∫ f (x, y) dxdy ≈ V0 |
|
N ′ |
= M (b − a) (d − c) |
|
N' |
|
, |
|
|
||||||||||
|
N |
|
N |
|
|
|||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
V0 |
− объем параллепипеда со сторонами (b − a) |
и |
(d − c) , |
и с |
|||||||||||||||
высотой |
M , равной или превышающей по величине максимум функции в |
|||||||||||||||||||
области |
G , так что во всей области |
0 ≤ f (x, y) ≤ M . |
В данном случае |
|||||||||||||||||
уже не прямоугольник, а параллепипед заполняется случайными точками (ξ, η, χ) , координаты которых имеют равномерное распределение в интервалах a < ξ < b , c < η < d , 0 < χ < M , и, если для произвольной точки (ξi , ηi , χi ) выполняется условие χi < f (ξi , ηi ) , то в счетчик для
N ′ добавляется единица.
В общем случае формула вычисления для k -кратных интегралов будет иметь вид
40
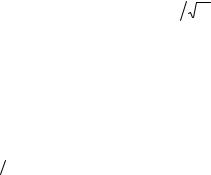
|
∫∫ ∫ f (x1, x2 , , xk ) dV |
≈ Vk |
N ' |
|
, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
G |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
Vk − k-мерный объем области интегрирования. |
|
|
|
|
|
|
|||||||||
|
Чем больше точек, тем точнее значение интеграла, но следует помнить, |
|||||||||||||||
что |
точность вычисления |
пропорциональна |
1 |
N , |
и |
для повышения |
||||||||||
точности в 10 раз нужно увеличить |
|
N в 100 раз и т.д.. |
|
|
|
|
||||||||||
|
Другой способ вычисления интегралов с помощью метода Монте-Карло |
|||||||||||||||
основан на вычислении среднего значения функции. |
Пусть |
|
ξ − случайная |
|||||||||||||
величина, равномерно распределенная в интервале |
(a,b) |
|
с плотностью |
|||||||||||||
вероятности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 (b − a) |
, |
|
|
a < x < b |
|
|
|
. |
|
||||||
|
pξ (x) = |
0 |
, в |
противном |
случае |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
Так как любая функция |
f (ξ) |
от случайной величины |
|
ξ также будет |
|||||||||||
случайной, то ее математическое ожидание равно |
|
|
|
|
|
|
||||||||||
|
M{f (ξ)}= b f (x) pξ (x) dx |
= |
1 |
|
b f |
(x) dx = |
|
I |
|
, |
||||||
|
|
b − a |
b − a |
|||||||||||||
|
∫ |
|
|
|
|
∫ |
|
|
|
|
||||||
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
I = ∫ f (x) dx |
. Отсюда видно, что интеграл |
I |
может быть вычислен |
||||||||||||
a
через математическое ожидание или среднее значение случайной величины f (ξ) , являющейся функцией равномерно распределенной случайной величины ξ . Используя оценку для среднего значения по выборочным значениям из N испытаний, получаем
|
|
|
|
|
b − a |
N |
|
I = (b − a) M{f (ξ)} ≈ |
(b − a) |
|
N |
= |
∑ f (ξi ) . |
||
f (ξ) |
|||||||
N |
|||||||
|
|
|
|
|
i=1 |
41
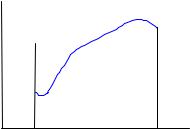
Описанный способ может также рассматриваться как модификация метода прямоугольников для вычисления интегралов. Правда, в данном случае область интегрирования не разбивается на множество интервалов с
шагом |
|
h , которые и служат основанием прямоугольников, |
||||||||
аппроксимирующих при суммировании значение интеграла. |
Наоборот, |
|||||||||
основание |
|
|
прямоугольников, |
|
|
|
|
|||
использующихся в данном методе, |
f(x) |
|
|
|||||||
равно |
|
полному |
интервалу |
|
|
|||||
|
|
|
|
|
||||||
интегрирования |
|
(b − a) , |
а вот |
|
|
|
|
|||
высота |
этих |
прямоугольников |
|
|
|
|
||||
случайна |
|
и |
равна |
значению |
|
|
|
|
||
функции |
|
f (xi ) |
в |
случайной |
|
|
|
|
||
точке xi |
интервала (a, b) . |
|
a x1 x2 |
|
x |
|||||
Будем |
"набрасывать" |
на |
b |
|||||||
|
|
|
|
|||||||
область |
|
интегрирования |
такие |
|
|
|
|
|||
случайные прямоугольники, а площадь каждого прямоугольника принимать за значение интеграла на каждом этапе. Из-за случайности высоты f (xi ) прямоугольников оценки значения интеграла будут также носить случайный
характер. |
Проведя |
N |
вычислений со |
случайными, |
равномерно |
|||||
распределенными |
в интервале |
(a, b) |
узлами |
xi |
, после |
усреднения |
||||
получим |
|
|
|
|
|
|
|
|
|
|
b |
|
b − a |
|
N |
|
|
|
|
|
|
∫ f (x) dx ≈ |
∑ f (xi ) . |
|
|
|
|
|||||
|
|
|
|
|
||||||
a |
|
N |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично могут быть вычислены и кратные интегралы. |
Например, |
|||||||||
для двойного интеграла формула вычислений имеет вид |
|
|
||||||||
b d |
|
|
|
(b − a)(d − c) |
N |
|
|
|
||
∫ ∫ f (x, y) dxdy ≈ |
∑ f (ξi ,ηi ) |
, |
|
|||||||
|
N |
|
|
|||||||
a c |
|
|
|
|
i=1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
42
где независимые случайные величины |
ξ , |
η |
равномерно распределены в |
|||||
интервалах a < ξ < b , |
c < η < d . |
|
|
|
|
|
||
Для интегралов произвольной кратности |
k аналогично будем иметь |
|||||||
|
|
Vk |
N |
|
|
|
|
|
∫∫ ∫ f (x1, x2 , |
, xk ) dV ≈ |
∑ f |
(x1i , x2i , |
, xki ) |
, |
|||
N |
||||||||
G |
|
i=1 |
|
|
|
|
||
|
|
|
|
|
|
|||
где Vk − k -мерный объем интегрирования, |
а x1i , x2i , |
, xki |
− случайная |
|||||
реализация значений независимых, равномерно распределенных в соответствующих интервалах интегрирования случайных величин
ξ1, ξ2 , , ξk .
В качестве примера рассмотрим вычисление интеграла
|
π |
π |
||
|
∫ |
|
||
J p (z) = |
1 |
|
|
cos(z sin x − p x) dx , |
|
0 |
|||
|
|
|
|
|
определяющего функции Бесселя первого рода порядка p от аргумента z Вычисления проведем методом "набрасывания" случайных прямоугольников.
Вариант программы:
Uses Crt; |
|
var |
|
p,z,S : real; |
{ p - порядок функции; z - аргумент функции } |
N : longint; |
{ N – число испытаний } |
Ch : char; |
|
label Rd,St,Fn,Cn; |
|
Function f(x : real) : real; |
|
begin |
|
f:=cos(z*sin(x)-p*x) |
|
end; |
|
43
Procedure MK(N : longint; var S : real); var a,h : real;
var l : longint;
begin |
|
|
a:=0; h := Pi; S:=0; l:=1; |
{ h=b-a =Pi-0 – интервал интегрирования } |
|
repeat |
|
|
|
S:=S+f(a+random*h); l:=l+1; |
|
until l > N; |
|
|
S:=h*S/N/Pi; |
{ S - значение интеграла } |
|
end; |
|
|
begin |
|
|
St : write('N= '); read(N); |
{ ввод параметров } |
|
|
write('p= '); read(p); |
|
|
write('z= '); read(z); |
|
|
MK(N,s); |
{ вычисление интеграла } |
|
writeln(' S = ', S); |
{ вывод значения интеграла } |
|
GoTo Cn; |
|
Rd : Ch:=ReadKey; |
|
|
|
case Ch of |
|
#27: GoTo Fn; |
{ проверка на <Esc> } |
|
#13: GoTo St; |
{ проверка на <Enter> } |
|
Else |
|
|
Cn : begin writeln('Введите <Enter> или <Esc>'); GoTo Rd; end; |
||
|
end; |
|
Fn : |
{ выход из программы } |
|
end. |
|
|
Расчет при N = 200 , p = 0 , z = 1 дает оценочное приближение
J 0 (1) = 0.76 ± 0.02 . Точное значение интеграла |
J 0 (1) = 0.7651977 . |
Видно, что приближение достаточно неплохое, однако, напомним, что метод наиболее эффективен для расчета многомерных интегралов.
44

ЗАДАЧИ
Задача 1
( Генератор равномерно распределенных псевдослучайных чисел )
Построить генератор псевдослучайных чисел, равномерно распределенных на интервале (0,1), на основе следующих соотношений:
U j+1 = [U j + U j−1](mod 4) |
, |
|
|
|
|
|||||
U 0 = π , U1 = 517 2−42 |
, |
|
|
|
|
|
||||
γ j |
= U j |
4 . |
|
|
|
|
|
|
|
|
Здесь: |
U j |
− некоторые вспомогательные величины (реальные!); |
|
|||||||
|
γ j |
− псевдослучайные |
числа, |
равномерно |
распределенные на |
|||||
|
|
|
интервале (0,1) ; |
|
|
|
|
|
||
|
знак |
(mod 4) |
означает, что берется остаток от деления на 4 суммы |
|||||||
|
[U j |
+ U j−1] . |
|
|
|
|
|
|
|
|
Построить гистограмму распределения чисел γ |
на интервале (0,1). |
|||||||||
Дополнительные вопросы: |
|
|
|
|
|
|
||||
а) Построить |
распределение |
случайных |
точек с |
координатами (γ1, γ 2 ) , |
||||||
(γ1, γ 2 ) , |
(γ1, γ 2 ) |
и т.д. |
на |
плоскости x − y . |
Как этот |
набор точек |
||||
заполнит квадрат со стороной равной 1 ? |
|
|
|
|||||||
б) Вычислить среднее значение γ |
и дисперсию σγ |
величины γ |
. Насколько |
|||||||
хорошо эти параметры соответствуют равномерному распределению на интервале
в) Как изменятся результаты, если U1 заменить на какое-нибудь другое число ?
45
Задача 2
Построить гистограмму распределения случайной величины η :
η = ξ1 + ξ2 + ξ3 + + ξn ,
где ξi ( i = 1, 2,..., n ) − случайные величины, равномерно распределенные на интервале (0,1). Построение выполнить для n = 2,4,6,8,10,12 .
Дополнительные вопросы:
а) Нанести на гистограмму график функции
|
1 |
e− |
( x−a)2 |
|
|
|
|
P(x) = |
|
2σ2 |
, |
|
|
||
2π σ |
|
|
|
|
|
|
|
где a = n 2 , σ = |
1 |
|
n 3 . |
|
|
||
|
|
2 |
|
|
|
|
|
Какие выводы можно сделать из сравнения гистограммы и графика |
|||||||
функции P(x) ? |
Как согласуется график и гистограмма при больших |
||||||
значениях |
x ? |
|
|
|
|
|
|
б) Построить |
на плоскости |
в |
координатах |
(x, y) распределение точек |
|||
(η1, η2 ) , (η3 , η4 ) , (η5 , η6 ) |
и т.д., где ηi |
( i = 1, 2,... ) − последовательно |
|||||
получаемые |
значения |
величины η . С чем ассоциируется получаемая |
|||||
картинка ?
Задача 3
( Распределение Гаусса из равномерного распределения )
Функция распределения плотности вероятности Гаусса в двумерном
пространстве (x, y) |
имеет вид: |
|
|
|
||||
|
1 |
|
|
2 + |
|
2 |
||
f (x, y) = |
|
exp |
− |
x |
y |
|
. |
|
|
2 |
|
2 |
|
||||
|
2πσ |
|
|
2σ |
|
|
||
|
|
|
|
|
|
|
||
46
Перейдя |
от |
|
декартовых |
|
|
координат |
(x, y) к |
полярным |
(r, ϕ) с |
|||||||||||||||||||||
использованием соотношений |
|
|
x = r cos ϕ , |
y = r sin ϕ , получим: |
|
|||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
r |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (r, ϕ) = |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2πσ |
exp |
|
2σ |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Будем интересоваться только распределением по r , тогда: |
|
|||||||||||||||||||||||||||||
~ |
2π |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f (r) = ∫ f (r,ϕ) r dϕ = |
σ |
2 |
|
r exp |
− |
2σ |
2 |
. |
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вспомним, |
если |
величина |
|
|
|
r |
имеет |
распределение |
плотности |
|||||||||||||||||||||
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
~ |
(r′)dr′ |
|
|
|
вероятности |
f (r) , |
то величина |
|
|
|
F(r) = ∫ |
f |
имеет равномерное |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
распределение |
|
от |
0 |
до |
|
|
1. |
|
|
|
Выполняя |
|
|
интегрирование, |
получаем: |
|||||||||||||||
r |
~ |
|
|
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F(r) = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f (r′)dr′ = |
1− exp |
− |
|
2σ |
2 |
|
|
, |
и после обратного |
преобразования: |
||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
r(F ) = σ |
− 2 ln(1− F ) . |
|
|
Так |
|
как |
величины |
(1− F) |
и F имеют |
|||||||||||||||||||||
одинаковое равномерное распределение от 0 до 1, то в последнем выражении
можем заменить (1− F) на F . В итоге имеем для |
r и, |
соответственно, |
||
для x, y : |
|
|
|
|
r(F) = σ − 2 ln F , |
|
|
|
|
x = r cos ϕ = σ |
− 2 ln F cos ϕ |
, |
|
|
y = r sin ϕ = σ |
− 2 ln F sin ϕ |
, |
|
|
где величина F равномерно распределена от 0 до 1, |
угол |
ϕ равномерно |
||
распределен от 0 до2π , а величины |
x и y имеют распределение Гаусса с |
|||
дисперсией σ2 . |
|
|
|
|
47

Используя вышеизложенный способ, построить датчик случайных чисел x , распределенных по нормальному закону с заданным стандартным отклонением σ .
1. Построить гистограмму распределения случайных чисел x . Нанести на гистограмму график функции
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
|
|
|
p(x) = |
|
|
|
2 |
|
|
||||
|
|
2π σ |
exp − |
2σ |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
Насколько |
хорошо |
график описывает гистограмму ? Наблюдается |
ли |
|||||||||
хорошее согласие графика и гистограммы при больших значениях |
x |
|||||||||||
( |
|
x |
|
>> σ ) |
? |
|
|
|
|
|
~ |
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
2. Вычислить среднеквадратичное отклонение σ и среднее значение |
||||||||||||
построенного распределения и сравнить их с заданными величинами моделируемого распределения. Исследовать точность совпадения вычисленных и заданных величин среднего и дисперсии в зависимости от числа N точек, использованных для моделирования нормального распределения.
Задача 4
( Определение числа π )
Определить с помощью метода Монте-Карло значение числа |
π . |
|
При произвольно выбранном числе N статистических испытаний для |
||
числа π получается приближенное вычисленное значение |
~ |
Построить |
πN . |
||
график зависимости относительной ошибки вычисления |
числа |
π , т.е. |
~ |
|
|
величины [πN − π]/ π , от числа N испытаний. |
|
|
Проанализировать полученный график и выбрать подходящий вид функции для его аппроксимации. Методом наименьших квадратов найти параметры аппроксимирующей функции.
48
