Добавил:

yermolenkoigor9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волгоградский государственный университет

Предмет:

Технология программирования

Файл:

stohastic

.pdf

Скачиваний:

Добавлен:

18.08.2019

Размер:

908.97 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

if max <> 0 then mash := MaxY / max; if max = 0 then mash:=0;

{Определение ширины прямоугольника для вывода интервала } shir := trunc((630-X0) / Ngist);

GetFillPattern(OldPattern);	{Цвет и стиль вывода гистограммы}
SetFillPattern(OldPattern,Color);

{Вывод гистограммы на экран } for i := 1 to NGist do begin

y := Y0 - round(MGist[i]*mash); x := X0 + round(Shir*(i-1)); bar(x+1, Y0, x + shir-1, y); end;

{Построение осей и разметки гистограммы } SetColor(white); line(X0-10,Y0,X0+NGist*shir+9,Y0); line(X0,Y0+10,X0,Y0-MaxY-10); line(X0-10,Y0-MaxY,X0+10,Y0-MaxY); line(X0+NGist*shir,Y0+10,X0+NGist*shir,Y0-10);

{Вывод значений максимума гистограммы, начального и конечного значений по оси X } Str(0,s);

MoveTo(X0-22,Y0-4); OutText(s); Str(max,s); MoveTo(0,Y0-MaxY-4); OutText(s); Str(Xstart:8:2,s); MoveTo(X0,Y0+14);

OutText(s);

Str(Xfin:8:2,s); MoveTo(X0+NGist*shir-64,Y0+14); OutText(s);

end;

end.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

При решении задач методом Монте-Карло, так же как и при обработке

экспериментальных данных, часто возникает один и тот же вопрос.

Пусть

мы решаем какую-нибудь задачу,

в которой некая физическая величина

зависит от аргумента

x ,

является функцией от

x :

т.е. y

y = y(x) .

Задав ряд значений аргумента xi , где i = 1,

, N , методом статистических

испытаний мы находим для каждой точки

соответствующие значения

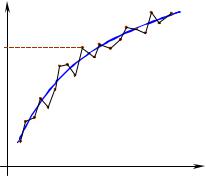
Если мы отложим на графике найденные точки и соединим их

= y

(xi ) .

отрезками прямых, то из-за статистического разброса значений

вместо

"гладкой" зависимости

получим изломанную от точки к точке

= y(x)

("зубастую") кривую (см. рис.).

Мы понимаем, что эта

изломанность возникает из-за

y=y(x)

статистических ошибок наших

вычислений величины

и не

y i

имеет

отношения

искомой

физической

зависимости

Поэтому в простейшем

y(x) .

случае

по найденному набору

точек

мы

можем,

например, "на глаз" провести

некоторую плавную (гладкую)

кривую, которая бы наилучшим образом аппроксимировала все точки

, и

принять эту гладкую зависимость за искомую зависимость

. Но в этом

y(x)

случае мы никогда не будем уверены, что провели такую гладкую

зависимость

"наилучшим"

образом и что

нельзя провести какую-нибудь

другую гладкую кривую, которая бы еще лучше аппроксимировала все точки

yi .

Пусть мы предполагаем, догадываемся или даже определенно знаем, что

искомая	зависимость	описывается	функцией			y = y(x, p1,..., pm ) , где
p1,..., pm	− некоторые параметры.		Попробуем подобрать параметры так,
чтобы функция y(x, p1,..., pm )			наилучшим			образом аппроксимировала
		~					что значит "наилучшим
(приближала) все точки yi . Естественен вопрос,
образом" ? Нам нужно, чтобы для каждой точки						xi		~	~
							значения yi		= y(xi ) и
yi = y(xi , p1,..., pm )		как можно	меньше		отклонялись			друг	от друга.
Возможны разные меры отклонения,				но наиболее часто в качестве такой
меры отклонения принимают величину					~	2	Тогда для наилучшего
				(yi − yi		) .
приближения всех точек последовательности					~	функцией		y(x, p1,..., pm )
					yi

мы должны потребовать, чтобы сумма квадратов отклонений по всем точкам была минимальна, т.е. чтобы величина

N	~
S = ∑(yi	~	2
S = ∑(yi	− yi	)
i=1
имела минимум.
Поскольку	yi		является функцией как от			xi , так и от параметров
p1,..., pm , величина			S	также	является	функцией от параметров
p1,..., pm :
			N		~
S = S( p1,	, pm ) = ∑(y(xi , p1,				~	2
S = S( p1,	, pm ) = ∑(y(xi , p1,				, pm ) − yi ) .

i=1

Чтобы функция S имела минимум, необходимо выполнение условий (см. ПРИЛОЖЕНИЕ):

∂S( p1,	, pm )	= 0	,
∂p1		= 0
∂p1
			,
∂S( p1,	, pm ) = 0 .
∂pm

Получается система m уравнений на m неизвестных параметров p1,..., pm . Если N ≥ m , то система может иметь однозначное решение,

хотя для произвольной нелинейной функции y(x, p1,..., pm ) такое решение в большинстве случаев может быть найдено только численными методами.

При найденных из решения		системы значениях параметров	p1,..., pm
функция	y(x, p1,..., pm )	наилучшим образом аппроксимирует
последовательность значений		~
последовательность значений		yi .

Рассмотренный способ называется методом наименьших квадратов (МНК) и широко используется при обработке результатов статистического моделирования, при обработке экспериментальных данных и в других случаях.

В ситуации, когда зависимость y(x) является линейной функцией

y = ax + b ,

приведенная выше система уравнений сильно упрощается. Действительно, в этом случае

p1 = a , p2 = b ,


N	~ 2
	~ 2
S = S(a,b) = ∑((axi + b) − yi )		,

i=1

и, соответственно, уравнения на минимум суммы квадратов отклонений имеют вид:

∂S		∂	N	~ 2		N	~
∂a	=		∑	((axi + b) − yi )	= 2	∑	xi ((axi + b) − yi ) = 0 ,
		∂a
			i=1			i=1

∂S		∂	N	~ 2	N	~
	=		∑((axi + b) − yi )		= 2∑((axi + b) − yi ) = 0 .
∂b	=	∂b	∑((axi + b) − yi )		= 2∑((axi + b) − yi ) = 0 .
∂b		∂b	i=1		i=1
			i=1		i=1

Решение этой системы двух линейных уравнений дает:

xy− x

a =

b = y − ax

x2 − (x)2

~ 1

∑

где

x =

, x

xi ,

y =

, xy =

xi yi .

i=1

Ниже приведен пример программы для вычисления коэффициентов a

и b

прямой

y = ax + b

наилучшего приближения по заданному массиву

из

статистически смоделированных

или

экспериментальных точек

i = 1,

, N :

(xi , yi ) ,

Program MNK ;

Var a, b, x, y, sum_x, sum_y

: Real ;

sum_xx, sum_xy

: Real ;

Begin

i, N

: Integer ;

Write(‘N=? : ’) ;

{ввод числа точек массива}

Readln(N) ;

sum_x:=0 ;

sum_y:=0 ;

sum_xx:=0 ;

sum_xy:=0 ;

For i:=1 to N do

Begin

Write(‘Input x : ’) ;

Readln(x) ;

{ввод значения x

точки}

Write(‘Input y : ’) ;

Readln(y) ;

{ввод значения y

точки}

sum_x:=sum_x + x ;

sum_y:=sum_y + y ;

sum_xx:=sum_xx + x*x ;

sum_xy:=sum_xy + x*y ; End ;

a:=( sum_x*sum_y - N*sum_xy )/(sum_x*sum_x - N*sum_xx) ;

y(x)

b:=(sum_y - a*sum_x)/N ; Writeln(‘a=’, a) ; Writeln(‘b=’, b) ;

Readln ; End.

Если зависимость − нелинейная, то в ряде случаев, используя функциональный масштаб, ее можно свести к линейной путем замены переменных. Так, например, если по расположению смоделированных или

экспериментальных точек на графике y(x) ожидается зависимость вида

y(x) = k eλx ,

то, прологарифмировав это выражение, можно перейти к

таким переменным q и

p , что связь между ними окажется линейной:

ln( y(x)) = ln(k) + λx ,

p = ln(y)

, q = x ,

b = ln k , a = λ ,

p(q) = aq + b .

В новом масштабе полученные данные должны укладываться на прямую

линию. Найдя методом наименьших квадратов коэффициенты

и b , как

изложено выше, можем найти выражения для коэффициентов k

λ :

λ =

x ln y

− x ln y

k = eln y −λ x .

− (x)2

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

На пластину из алюминия толщиной D = 75 см перпендикулярно ее поверхности падает пучок моноэнергетических тепловых нейтронов. Вероятность свободного пробега нейтрона в веществе до взаимодействия равна p(l) = µ e−µ l , где = 0.0981 см-1.


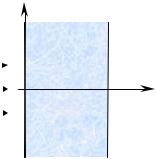
В результате взаимодействия с							y
веществом	нейтрон			либо
поглощается	с		вероятностью			n
pa = 0.141,	либо		рассеивается		с			x

вероятностью	ps	= 0.859 . Считать,

						0		D
что задача двумерна и рассеяние

нейтронов происходит изотропно					в
плоскости рисунка.
Нарисовать		набор		траекторий

движения нейтронов в пластине.

Построить гистограмму распределения нейтронов, прошедших через пластину, в зависимости от угла вылета из пластины.

Решение

Сложный случайный процесс прохождения нейтронов через вещество будем рассматривать как последовательность конечного числа элементарных случайных событий. Такими событиями в данном случае будут: движение нейтрона без взаимодействия на некотором пути, взаимодействие какоголибо типа (поглощение или рассеяние) и, если нейтрон не поглощается, снова движение до следующего взаимодействия. Зная вероятность каждого из этих событий, можно смоделировать траекторию нейтрона в пластине. Повторяя этот процесс для достаточно большого числа нейтронов, можно определить требуемые характеристики процесса прохождения нейтронов через пластину.

Так как задача симметрична относительно оси	y , будем считать что
движение каждого нейтрона начинается в точке	0 . Тогда алгоритм
прослеживания траекторий может быть таким:

1. Инициализируем начальное положение нейтрона при входе в пластину: x = 0 , y = 0 , ϕ = 0 (угол ϕ отсчитывается от оси x ).

2.Моделируем движение нейтрона без взаимодействия (свободный пробег). Так как плотность распределения длины свободного пробега

нейтрона вдоль заданного направления

описывается

экспоненциальной функцией распределения					p(l) = µ e−µl , то длина
пробега до	взаимодействия	l = −	1	ln(γ)	.	Определяем новые
			µ

координаты	положения нейтрона:		x = x + l cos ϕ , y = y + l sinϕ ,

ϕ= ϕ .

3.Проверяем, не вышел ли нейтрон за границы пластины ? Если вышел

( x > D ) , то вносим в гистограмму точку с углом ϕ и переходим к розыгрышу траектории следующего нейтрона на п.1. Если нейтрон не вышел за границы пластины ( x ≤ D ) , то переходим к следующему пункту.

4.Розыгрыш типа взаимодействия нейтрона с веществом. Определяем, какой процесс произошел − поглощение или рассеяние. Для этого получаем очередное случайное число γ и сравниваем его со значением

вероятности поглощения нейтрона pa . Если γ ≤ pa , то это означает,

что произошло поглощение нейтрона, поэтому процесс прослеживания текущей траектории заканчивается и переходим к п.1 для розыгрыша движения следующего нейтрона. Если γ > pa , то произошло рассеяние нейтрона и переходим к пункту 5.

5.Определение параметров рассеяния нейтрона. Считая рассеяние

нейтрона изотропным, определяем угол рассеяния по формуле ϕ = 2πγ , так как рассеяние во все стороны равновероятно. Теперь, определив новое направление движения нейтрона, возвращаемся к п.2 для розыгрыша движения нейтрона в этом направлении до следующего взаимодействия.

6.Повторяем описанный процесс необходимое число раз, соответствующее числу нейтронов, упавших на пластину.

Вариант программы:

uses Gisto,Graph;

const

MashX = 2; { Масштабный коэффициент по X для вывода на экран } MashY = 1.2; { Масштабный коэффициент по Y для вывода на экран } NGist = 60; { Число интервалов гистограммы }

Mu = 0.0981; { Mu - коэффициент поглощения нейтрона } Pa = 0.0141; { Pa - вероятность поглощения нейтрона } D = 80.; { D - толщина пластины }

var

Gd, Gm, I, N : Integer;

Xscr, Yscr, Xscr0, Yscr0 : Integer; OldPattern : FillPatternType;

x, y, Lpr, Fi : real;

label P1, P2, P3, P4, P5, OutGist;

begin

writeln('Введите число нейтронов N = '); readln(N);

{Переходим в графический режим }

Gd := Detect; InitGraph(Gd, Gm, 'с:\tp\bgi'); if GraphResult <> grOk then begin

writeln (' Graph error or BGI driver not found. '); Halt;

end;

{Рисуем пластину в центре экрана } GetFillPattern(OldPattern);

SetFillPattern(OldPattern,7); { стиль и цвет для вывода пластины } Bar(320-round(D*MashX/2), 0, 320+round(D*MashX/2), 479);

Randomize;	{ подкрутка Random }
i := 0;	{ очистка счетчика числа нейтронов }
InitGist(NGist,-Pi/2,Pi/2);	{ инициализация гистограммы в диапазоне
P1:	углов от -Pi/2 до Pi/2 }
P1:

{Инициализируем начальные координаты и угол движения нейтрона } i := i + 1;

if (i > N ) then goto OutGist; { проверка на исчерпание числа нейтронов } x := 0; y := 0; Fi := 0;

Xscr0 := 320-round(D*MashX/2); Yscr0 := 240;

MoveTo(Xscr0,Yscr0);	{ установка точки на экране в позицию x=0, y=0 }
SetColor (i);	{ установка цвета вывода траектории }

P2:

{ Определяем длину свободного пробега и новые координаты нейтрона}

Lpr := - ln(Random)/Mu;	{ длина пробега }
x := x + Lpr*cos(Fi);	{ новая координата x }
y := y + Lpr*sin(Fi);	{ новая координата y }

{Определяем экранные координаты и рисуем траекторию } Xscr := Xscr0 + round(x*MashX);

Yscr := Yscr0 + round(y*MashY); LineTo(Xscr,Yscr);

P3:

{Проверка выхода за границы пластины }

if (x < 0 ) then GoTo P1;	{ выход за левую границу пластины,
	переходим к следующему нейтрону }
if (x > D) then begin	{ выход за правую границу }
if (Fi > Pi) then Fi := Fi - 2*Pi;	{ коррекция диапазона по углам }
InGist(Fi);	{ заносим точку в массив гистограмм }
GoTo P1;
end;

P4:

{ Проверка на поглощение или рассеяние нейтрона }

if (Random <= Pa) then GoTo P1; { поглощение нейтрона }

P5:

{Рассеяние нейтрона, розыгрыш угла рассеяния } Fi := 2*Pi*Random;

GoTo P2;

OutGist:

write(' Вывод гистограммы <Enter> ? ');

readln;	{ ожидание <Enter> }
ClearDevice;	{ очистка экрана перед выводом гистограммы }
Gistogram(13);	{ вывод гистограммы }
readln;	{ ожидание <Enter> }
CloseGraph;
end.

Для построения гистограмм в программе используется описанный выше модуль Gisto (текст модуля и его правильное применение приведены в предыдущем примере).

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в папке Stohastic

#
18.08.2019908.97 Кб9stohastic.pdf
#
18.08.20195.54 Mб22Методичка_Стохастика_Федунов.doc