
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР
МОДЕЛИРОВАНИЕ
ФИЗИЧЕСКИХ
ЯВЛЕНИЙ
НА ЭВМ
Часть V
Статистическое
моделирование
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР
Кафедра физики
Кайран Д.А., Кандауров И.В., Краснов А.А., Мезенцев Н.А., Мешков О.И., Пиндюрин В.Ф., Скарбо Б.А.
МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ЯВЛЕНИЙ НА ЭВМ
Методическое пособие
Часть V
Статистическое моделирование
Новосибирск
2000
Пособие является составной частью учебно-методических материалов, предназначенных для учащихся Специализированного учебно-научного центра Новосибирского государственного университета (СУНЦ НГУ − бывшая Физико-математическая школа им. М.А.Лаврентьева), занимающихся на спецкурсе "Моделирование физических явлений на ЭВМ". В настоящем пособии рассмотрены основы метода статистического моделирования (метод Монте-Карло) для решения физических, технических и других задач. Даются основные вероятностные понятия, способы получения случайных величин и обработки получаемых результатов. Приводится набор задач для самостоятельного решения.
Рецензенты:
доцент кафедры физики СУНЦ НГУ
Харитонов В.Г.
профессор кафедры теор. физики НГУ, к.ф.-м.н.
Коткин Г.Л.
Новосибирский государственный университет, 2000
Подготовлено при поддержке ФЦП "Интеграция", проект "Современные компьютерные технологии в ранней профессиональной ориентации и подготовке физиков-исследователей" (рег. № 274)
1

СОДЕРЖАНИЕ |
|
Введение |
3 |
Основные вероятностные понятия |
4 |
Основные принципы метода статистического моделирования |
12 |
Получение равномерно распределенных случайных чисел |
15 |
Моделирование дискретных случайных величин |
17 |
Моделирование непрерывных случайных величин |
20 |
Обработка результатов моделирования |
23 |
Метод наименьших квадратов |
30 |
Пример решения задачи методом статистического моделирования |
34 |
Вычисление интегралов методом Монте-Карло |
39 |
Задачи |
45 |
Рекомендуемая литература |
79 |
Приложение |
80 |
2
ВВЕДЕНИЕ
Настоящее пособие посвящено решению задач методом статистических испытаний или, как его еще называют, методом Монте-Карло. Название "Монте-Карло" происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом для игры в рулетку, и символизирует случайность процесса, как и при игре в рулетку. Возникновение и развитие этого метода стало возможным только после появления ЭВМ, поскольку моделирование случайных величин вручную очень трудоемко.
На первый взгляд может показаться странным совместимость случайности со строго детерминированной работой ЭВМ. Действительно, случайный сбой даже одного бита в ЭВМ может привести к совершенно неправильным результатам вычислений. Тем не менее, как мы увидим дальше, такой "симбиоз" вполне возможен и очень плодотворен.
Метод Монте-Карло весьма красив и прост по своим принципам и широко используется для расчетов в физике и технике (ядерная физика, физика элементарных частиц и ускорителей, взаимодействие различных излучений с веществом, геофизика, расчет качества и надежности изделий и т.д.). В некоторых случаях методом Монте-Карло решаются задачи, которые в принципе могут быть решены другими методами; в других же случаях метод Монте-Карло оказывается единственным для решения задач. Метод особенно хорош там, где не требуется очень высокой точности получаемых результатов.
Здесь мы будем рассматривать в основном физические и технические задачи, однако, нужно помнить, что метод статистических испытаний успешно применяется в математике, теории игр, теории массового обслуживания, теории передачи сообщений и обнаружения и т.д., поэтому приобретенные здесь навыки Вы сможете с успехом применить и в других областях деятельности.
3
ОСНОВНЫЕ ВЕРОЯТНОСТНЫЕ ПОНЯТИЯ
Случайным опытом или экспериментом называется процесс, при котором возможны различные исходы, так что нельзя заранее предсказать, каков будет результат. Величина X , представляющая собой результат случайного опыта, называется случайной величиной. Непостоянство результата такого опыта может быть связано с наличием случайных ошибок измерений или со статистической природой самой измеряемой величины (например, процесс распада радиоактивного вещества). Будем обозначать отдельные значения, которые принимает случайная величина (не обязательно численные), как Xi , где i = 1, 2, , n . Любая функция от Xi будет также случайной величиной.
Случайные величины бывают дискретные и непрерывные, одномерные (зависящие от одной переменной) или многомерные (зависящие от двух и более переменных).
Полной характеристикой случайной величины X с вероятностной точки зрения является ее закон распределения, т.е. заданная в той или иной форме связь между возможными значениями случайной величины и вероятностями их появления.
Естественной формой закона распределения дискретной случайной
величины |
|
X , принимающей дискретный набор значений X1 , X 2 , ..., X n |
|||||||
с соответствующими вероятностями P1, P2 , ..., Pn , является таблица |
|||||||||
X = |
X |
|
X |
|
... |
X |
|
, |
|
|
|
1 |
|
2 |
... |
P |
n |
||
|
|
P |
P |
|
|
||||
|
|
|
1 |
2 |
|
n |
|
|
|
где X1 , X 2 , ..., X n |
− возможные значения величины X , а P1, P2 , ..., |
Pn |
|
n |
|
− соответствующие им вероятности, причем, ∑Pi =1 . |
|
|
|
i =1 |
|
Универсальной |
формой закона распределения (непрерывных |
и |
дискретных величин) является функция распределения вероятностей − это такая функция F(x) , значение которой в точке x равно вероятности P
4

того, что при проведении опыта значение случайной величины X окажется меньше, чем x :
F(x) = P(X < x) .
Основные свойства функции распределения вероятностей следующие:
1) |
числовые значения заключены в пределах 0 ≤ F(x) ≤ 1 ; |
|
2) |
если x1 ≤ x2 , то |
F (x1) ≤ F (x2 ) , т.е. F(x) − неубывающая функция; |
3) |
F(x) → 0 при |
x → −∞ , F(x) → 1 при x → ∞ . |
F(x) |
(b) |
F(x) |
(a) |
1 |
|
1 |
|
|
x |
|
x |
Если случайная величина дискретна, то ее функция распределения представляет собой ступенчатую функцию (рис. a ), а у непрерывных случайных величин функция распределения также непрерывна (рис. b ).
Функцию распределения вероятностей F(x) непрерывной случайной величины можно представить в виде интеграла от некоторой неотрицательной функции f (x) :
x
F(x) = ∫ f (u) du .
−∞
Функция f (x) называется плотностью распределения вероятности. Основные свойства плотности вероятности таковы:
|
|
dF(x) |
x |
|
1) |
f (x) = |
; F(x) = ∫ f (u) du ; |
||
dx |
||||
|
|
−∞ |
||
|
|
|
5
∞
2) ∫ f (u) du = 1 ;
−∞
3)плотность вероятности пропорциональна вероятности события
( x ≤ X ≤ x + dx ) .
Кроме закона распределения, случайную величину характеризуют значениями некоторых параметров, определяющих наиболее существенные особенности ее распределения. Наиболее часто используемыми параметрами распределения являются математическое ожидание или среднее значение случайной величины, а также дисперсия случайной величины.
Математическим ожиданием или средним значением дискретной случайной величины называется сумма всех возможных значений xi случайной величины X , умноженных на соответствующие вероятности:
n |
|
n |
M{X} ≡ x = ∑ xi P(X = xi ) = ∑ xi Pi . |
||
i=1 |
|
i=1 |
Заметим, что |
x |
является не случайной, а определенной, |
детерминированной величиной.
Так как функция от случайной величины является также случайной величиной, то математическое ожидание функции Y = H ( X ) определяется следующим образом:
n |
n |
M{H (X )} = ∑ H (xi ) P(X = xi ) = ∑H (xi ) Pi . |
|
i=1 |
i=1 |
Для непрерывных случайных величин будем иметь
∞
M{X} ≡ x = ∫ x f (x) dx
−∞
и
∞
M{H (X )} = ∫ H (x) f (x) dx .
−∞
6

Важной характеристикой отклонения или разброса случайной величины от ее среднего значения является дисперсия случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины X от своего среднего значения:
D{X} ≡ σ2 (X ) =
= M{(X − M{X})2 } = M{(X − x)2 } ≡ M{X 2 } −
Положительный квадратный корень из дисперсии
называется стандартным или среднеквадратичным отклонением*).
Среднеквадратичное отклонение количественно показывает, насколько
сильно |
значения случайной величины X |
разбросаны вокруг среднего |
|||||
значения x . |
|
|
|
|
|||
В качестве примера дискретной случайной величины рассмотрим числа, |
|||||||
выпадающие при бросании игрального кубика. |
|
|
|
||||
Пусть мы |
N раз бросили игральный кубик и получили |
N1 , N2 , N3 , |
|||||
N4 , N5 , N6 |
выпаданий значений 1, 2, 3, 4, 5, 6, соответственно. Тогда |
||||||
говорят, |
|
что |
вероятность выпадания |
какого-нибудь |
числа |
i |
|
( i = 1, 2, 3, 4, 5, 6 ) приближенно равна |
|
|
|
||||
Pi ≈ |
Ni |
|
, |
|
|
|
|
N |
|
|
|
||||
|
|
|
|
|
|
||
т.е. Pi |
равна доле числа случаев, в которых выпало значение |
i , от полного |
|||||
числа бросаний. Знак приближенного равенства означает, что если мы повторим еще N бросаний, то получим, вообще говоря, другое значение Ni .
Соотношение для вероятности становится точным в пределе, когда N → ∞ :
Pi = lim |
Ni |
. |
|
||
N →∞ N |
|
|
*) Часто используют также эквивалентный термин квадратичное отклонение.
7
В нашем случае, если кубик "честный", вероятности выпадания значений
1, 2, 3, 4, 5, 6 |
равны |
|
|
|
|
|
|
|
|
|
|
||||
|
P |
= P |
= P |
= P = P |
= P = 1 . |
|
|
|
|
|
|||||
1 |
2 |
|
3 |
|
4 |
5 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно также, что |
|
|
|
|
|
|
|
|
|
||||||
1 |
6 |
N = |
6 |
P = |
1 . |
|
|
|
|
|
|
|
|||
|
N |
∑ |
|
|
|
|
|
|
|
||||||
|
∑ |
i |
|
i |
|
|
|
|
|
|
|
|
|
||
|
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычислим математическое ожидание |
M{X} и дисперсию |
D{X} для |
|||||||||||||
игрального кубика: |
|
|
|
|
|
|
|
|
|
|
|||||
M{X} =1 |
1 |
+ 2 1 |
+ |
3 1 + |
4 |
1 + 5 |
|
1 |
+ 6 1 |
= 3.5 , |
|
||||
|
|
|
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
6 |
|
|
D{X} = M{X 2 } − (M{X})2 |
= |
|
|
|
|
|
|
||||||||
= 12 1 |
+ 22 |
1 |
+ 32 |
|
1 + 42 |
1 |
+ 52 |
|
1 |
+ 62 |
1 − (3.5)2 |
= 2.917 . |
|||
|
|
6 |
|
|
6 |
|
|
6 |
6 |
|
|
6 |
|
6 |
|
В качестве примеров непрерывных случайных величин рассмотрим два весьма важных непрерывных распределения.
Пример 1. |
Равномерное распределение. |
|
|
|
|
||||||
Случайная величина |
X имеет равномерное распределение на интервале |
||||||||||
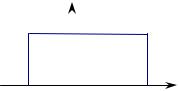
( a, b ) , если ее плотность вероятности задается следующим образом: |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
, если |
a < x |
< b , |
|
|
|
p(x) |
|
|
|
|
|
|
|
||||||
p(x) = |
|
|
|
|
|
|
|
|
|||
b − a |
|
|
|
|
|
|
|
||||
|
0 |
|
, в противном случае . |
|
|
|
1/(b−a) |
||||
|
|
|
|
|
|
|
|
|
|
||
Заметим, что в разной литературе |
|
|
|
|
|||||||
несколько |
|
по-разному |
определяется |
|
|
|
x |
||||
равномерное |
|
распределение |
на |
|
|
|
|||||
|
a |
0 |
b |
||||||||
заданном интервале. Часто плотность |
|||||||||||
|
|
|
|
||||||||
8
